Axiomes de hilbert

David Hilbert

Euclide a rassemblé dans un livre fondateur (Les Éléments) toutes les connaissances géométriques de son temps sous la forme d’une théorie axiomatique. Il a laissé son nom à la géométrie euclidienne qui utilise son cinquième postulat, à la géométrie non-euclidienne qui ne l'utilise pas, et aux espaces euclidiens. Ce livre contient une base axiomatique pour construire sa géométrie.

Cette base axiomatique est néanmoins imparfaite: pour démontrer rigoureusement les théorèmes associés à cette géométrie, il est nécessaire d'admettre comme vraies des hypothèses supplémentaires implicites.

David Hilbert construit une axiomatique correspondant à l'idée qu'Euclide se fait de la géométrie. C'est l'objet de cet article.

Contexte

Les axiomes de Hilbert sont formés par 20 assertions (à l'origine 21), David Hilbert les a proposées dans un article de 1899 comme fondation rigoureuse pour un traitement moderne de la géométrie euclidienne. Deux autres axiomatisations de la géométrie euclidienne existent par ailleurs : celle de Tarski et celle de George Birkhoff.

La représentation d'Euclide

Angles et longueurs chez Euclide

Preuve d'Euclide

Pour une animation, cliquer sur la flèche

Pour une image fixe, cliquer sur la flèche

Euclide définit dans sa géométrie les notions de longueur et d'angle. Il est intéressant de voir ce qu'Euclide présuppose implicitement lorsqu'il les utilise.

Les définitions d'angle, d'angle droit, d'angle obtus, d'angle aigu, apparaissent dès les premières définitions du Livre I des Éléments.

Un angle plan est l'inclinaison mutuelle de deux lignes qui se touchent dans un plan, et qui ne sont point placées dans la même direction.

Lorsque les lignes, qui comprennent ledit angle, sont des droites, l'angle se nomme rectiligne.

Lorsqu'une droite tombant sur une droite fait deux angles de suite égaux entre eux, chacun des angles égaux est droit.

L'angle obtus est celui qui est plus grand qu'un droit.

L'angle aigu est celui qui est plus petit qu'un droit.

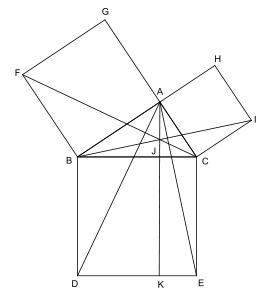
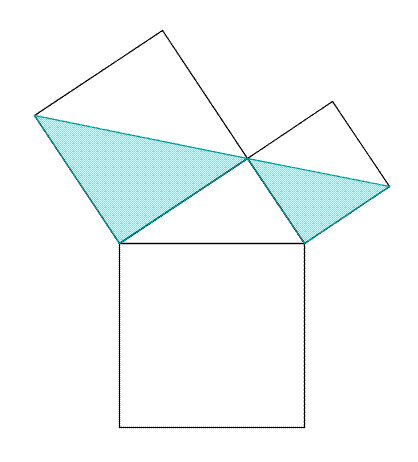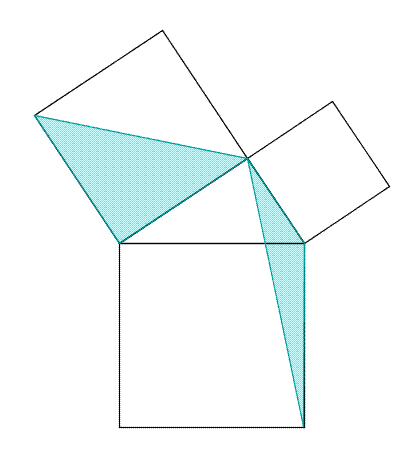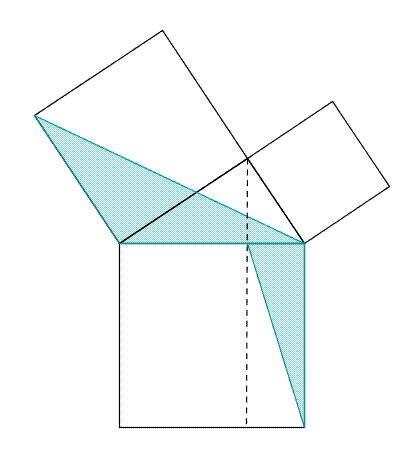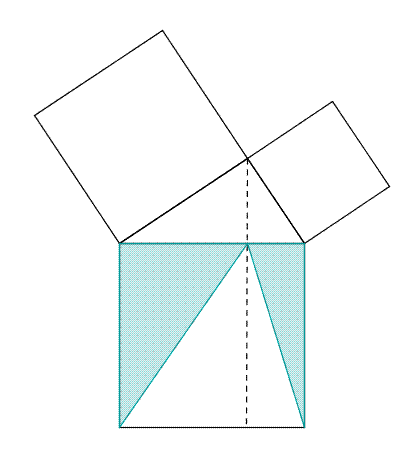
Cependant Euclide ne précise pas comment il définit l'égalité ou la comparaison de deux angles, pas plus qu'il ne définit l'égalité de deux longueurs. En fait, il apparaît qu'Euclide utilise implicitement la conservation des angles ou des longueurs de segments lorsque ceux-ci sont déplacés d'une position à l'autre, même si la notion de déplacement n'apparaît pas non plus explicitement dans les Éléments. Ainsi, pour montrer qu'un triangle ABC, ayant deux côtés AB et AC de même longueur, est tel que les angles B et C sont égaux, Euclide superpose les triangles ABC et ACB. Il suppose donc implicitement que, dans cette superposition, longueurs et angles sont conservés. La géométrie d'Euclide est donc ce qu'on pourrait appeler une géométrie des figures rigides.

La figure du paragraphe illustre le mécanisme d'une preuve classique dans la démonstration d'un théorème, celui de Pythagore. Les triangles AEC et IBC sont semblables car le deuxième est la rotation d'un quart de tour du premier. Un triangle est donc une figure rigide qui possède une aire invariante par rotation.

Nombre et géométrie

Cas où le corps n'est pas complet

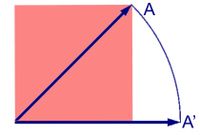
Pour Euclide, le nombre est rationnel et répond à toutes les bonnes propriétés nécessaires. Dans son axiomatique, la question ne se pose pas. La connaissance actuelle des nombres montre que, s'il est possible de construire une géométrie sur les rationnels, le résultat n'est néanmoins pas celui espéré. Le corps de nombre n'est alors pas complet. La figure associée au paragraphe illustre alors l' anomalie, la rotation d'un quart de tour du segment orienté de la diagonale n'est plus un segment. En effet, le point A' n'existe pas. Ce segment possède une longueur de √2.

Une autre configuration, cette fois moins exotique, peut aussi se produire. En l'absence de précision, le corps de nombre peut être celui des complexes. Là encore, la géométrie est différente. Cette situation, compatible avec les axiomes d'Euclide, est bien connue à l'époque de la rédaction de l'article de Hilbert.

Rien, dans les axiomes ne garantit la présence d'un corps réel. En fait, la seule indication sur le corps de nombres sous-jacent est le troisième postulat, qui indique l'existence d'un cercle de rayon la longueur d'un segment.

Unicité de la géométrie

Une géométrie non euclidienne

Une idée fréquente pendant plus des deux millénaires qui ont suivi l'édition des Éléments d'Euclide est le fait qu'il n'existe que deux uniques géométries, celle du plan euclidien, et celle de l'espace euclidien.

Elle se traduit par le statut donné au cinquième postulat, dit de la parallèle. Tel que formulé par Proclos, celui-ci stipule que « dans un plan, par un point distinct d'une droite d, il n'existe qu'une unique droite parallèle à d.» Si, comme on l'a cru jusqu'au début du XIX^e siècle l'unicité de la géométrie euclidienne est vraie, alors le cinquième postulat ne serait qu'un théorème, encore à l'état de conjecture. Il ne manquerait que le talent d'un mathématicien pour la démontrer, mais la proposition serait vraie et son statut de postulat ne serait que provisoire.

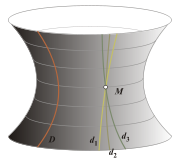Il existe une infinité de droites qui, comme d1, d2 et d3, passent par le point M et sont parallèles à la droite D. Exemple de géométrie hyperbolique ne respectant pas le 5^e postulat d'Euclide.

Mais lorsque Hilbert axiomatise la géométrie euclidienne, on sait déjà qu'il y a des géométries qui ne respectent pas le 5^e postulat. Dans son programme d'Erlangen, Felix Klein ordonne les différentes géométries: les espaces de Nicolaï Lobatchevsky et Bernhard Riemann ne vérifient pas le 5^e postulat.

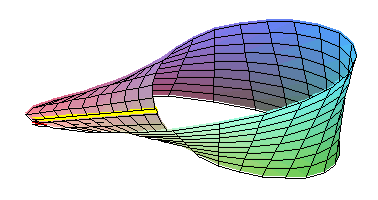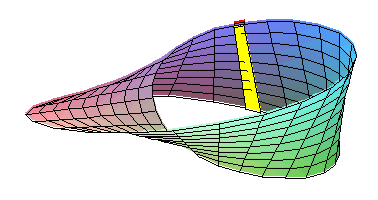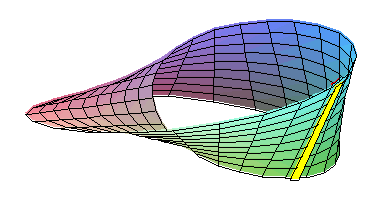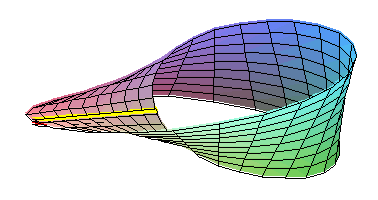
D'autres cas sont connus: Klein a construit un espace, celui de la figure qui respecte le cinquième postulat, mais qui n'est pas orientable. Dire qu'un espace est « orientable » signifie que la droite et la gauche existent. Dans un espace euclidien, une main droite et une main gauche ne sont jamais superposables, il est impossible de les faire coïncider sans utiliser une symétrie, c’est-à-dire une transformation équivalente à celle d'un miroir. La figure du paragraphe montre que cet état de fait n'est pas vrai dans toutes les géométries. Ainsi, la règle de la figure, jaune sous le plan et rouge au dessus, par un mouvement continu devient rouge sous le plan et jaune au dessus. Ce qui est impossible dans un plan euclidien.

Analyse de Hilbert

Ces présuppositions ont été mises en évidence à la fin du XIX^e par Pasch et Hilbert. Celui-ci a donné, avec Les fondements de la géométrie, un exposé axiomatique complet et rigoureux, s'attachant à clairement identifier tous les axiomes implicitement utilisés dans la géométrie traditionnelle.

Angle et longueur

Une des notions fondamentales de la théorie d’Euclide est donc celle d’égalité, ou congruence entre figures. Deux figures sont égales si elles peuvent représenter deux positions différentes d’un même corps rigide. Pour savoir si deux distances AB et CD sont égales, on peut repérer deux points E et F sur une règle rigide, et s’assurer que EF peut être ajusté à la fois sur AB et sur CD. Cela conduit à un problème de circularité : au sens géométrique, une règle est rigide lorsque les distances entre ses points ne varient pas au cours d'un déplacement. Mais pour savoir que deux distances sont égales, on se sert d’un corps rigide qu'on déplace.

David Hilbert, dans ses Fondements de la géométrie, mettra en évidence ce cercle vicieux. Pour y remédier, il introduit de nouveaux axiomes dévoilant les présupposés implicites d'Euclide. Ces axiomes donnent les propriétés qu'on souhaite voir vérifiées par des figures congruentes. Par exemple, on souhaite que la règle de transitivité soit respectée : si AB et CD ont la même longueur, et que CD et EF ont aussi la même longueur, alors AB et EF doivent avoir même longueur. Par ailleurs, un des axiomes de Hilbert relie congruence de segments et congruence d'angles et constitue le premier cas d'égalité des triangles : si [AB] est congruent à [A'B'], [AC] à [A'C'] et l'angle BAC à à l'angle B'A'C', alors [BC] est congruent à [B'C']. A noter, que cette propriété, qui est un théorème chez Euclide est devenu un axiome chez Hilbert. C'est qu'Euclide suppose implicitement que les déplacements conservent la congruence. Cette supposition, mise à jour par Hilbert, revient en fait à admettre la validité du théorème. Hilbert déduit de cet axiome les autres cas d'égalité des triangles, l'existence de l'angle droit et la congruence entre eux de tous les angles droits, cette dernière propriété étant un axiome chez Euclide.

Nombre et géométrie chez Hilbert

Hilbert sait parfaitement que les corps de nombres ne sont pas uniques. Il sait aussi que l'idée des antiques sur le corps ayant les bonnes propriétés est fausse. Les nombres rationnels ne possèdent pas les propriétés requises pour modéliser convenablement notre espace.

Le bon corps est celui des nombres réels. Ce corps a été axiomatisé de manière particulièrement simple par Hilbert: c'est l'unique corps archimédien complet.

Le choix axiomatique de Hilbert, pour une question d'élégance, ne fait pas plus référence aux nombres que la construction antique. Seul deux axiomes sont ajoutés, un correspond à la propriété archimédienne, l'autre à la complétude emprunté au formalisme de Cauchy repris par Cantor. Ces deux axiomes assurent l'unicité du corps sous-jacent.

Non unicité de la géométrie

Hilbert montre que l'axiome du premier cas d'égalité des triangles ne peut se déduire des autres axiomes. On peut en effet définir une géométrie (non archimédienne) vérifiant tous les axiomes de la géométrie de Hilbert sauf le premier cas d'égalité des triangles. Cette géométrie présente les anomalies suivantes :

• On ne dispose pas de l'inégalité triangulaire.
• Les cas d'égalité des triangles ne sont plus valables.
• On peut avoir un triangle ayant deux angles égaux, mais dont les deux côtés ne sont pas égaux.
• La symétrie par rapport à une droite ne conserve pas nécessairement les longueurs.
• La notion d'aire d'un triangle (base × hauteur/2) n'est plus définie.
• On peut trouver deux carrés équidécomposables (i.e. qui peuvent être décomposés en triangles congruents), dont l'un est intérieur à l'autre.

L'axiomatique de Hilbert n'inclut qu'une unique géométrie, celle que les antiques imaginaient. Elle ne contient aucune anomalie et répond donc précisément à la pensée d'Euclide.

La base axiomatique

Il existe trois objets primitifs sur lesquels la base axiomatique s'applique. Ces objets ne sont pas définis, il s'agit de point, de droite et de plan.

Les axiomes sont regroupés en cinq catégories: l'association, l'ordre, la congruence, la continuité et les parallèles.

Trois concepts sont associés à cette axiomatique. Celui de l'association définit le mot contient, il correspond aux notions est élément de et est inclus dans de la théorie des ensembles. Celui de l'ordre correspond à une relation binaire entre un couple de points et un point, il apparaît dans les expressions entre et permet de définir les segments. La congruence, qui correspond à trois relations d'équivalence pour les couples de points, les triangles et les angles.

Les points, droites et plans sont considérés comme distincts par défaut, les cas contraires sont précisés dans la suite de l'article.

I. Association

I.1: Soient deux points, il existe une droite passant par ces deux points.

I.2: Soient deux points, il n'existe qu'une unique droite passant par ces deux points ; i.e. la droite décrite en I.1 est unique.

I.3: Une droite contient au moins deux points, et pour une droite donnée, il existe au moins un point non contenu dans la droite.

I.4: Soient trois points non contenus dans une droite, il existe un plan contenant ces trois points. Tout plan contient au moins un point.

I.5: Soient trois points non contenus dans une droite, il n'existe qu'un unique plan contenant ces trois points.

I.6: Soient deux points contenus dans une droite d et dans un plan α, alors α contient tous les points de d.

I.7: Si deux plans α et β contiennent tout deux un point A, alors l'intersection de α et β contient au moins un autre point.

I.8: Il existe au moins quatre points non coplanaires.

II. Ordre

II.1: Si un point B est entre les points A et C, B est aussi entre les points C et A, et il existe une droite contenant les trois points A,B,C.

II.2: Soient deux points A et C, il existe un point B élément de la droite AC tel que C se situe entre A et B.

II.3: Soient trois points contenus dans une droite, alors un et un seul se situe entre les deux autres.

II.4: Axiome de Pasch. Soient trois points A, B, C non alignés et soit une droite d contenue dans le plan ABC mais ne contenant aucun des points A, B, C: Si d contient un point du segment AB, alors d contient aussi soit un point du segment AC soit un point du segment BC.

III. Congruence

III.1: Soient deux points distincts A, B et un point A' élément d'une droite d, il existe deux et deux uniques points C et D éléments de la droite d, tel que A' se situe entre C et D, et AB est congru à CA' ainsi qu'à DA' .

III.2: La relation de congruence est transitive, c’est-à-dire, si AB est congru à CD et si CD est congru à EF, alors AB est congru à EF.

III.3: Soient une droite d contenant les segments adjacents AB et BC et une droite d' contenant les segments adjacents A'B' et B'C' . Si AB est congru à A'B' et BC est congru à B'C' , alors AC est congru à A'C' .

III.4: Soient un angle ABC et une demi-droite B'C' , il existe deux et seulement deux demi-droites, B'D et B'E,tel que l'angle DB'C' est congru à l'angle ABC et l'angle EB'C' est congru à l'angle ABC.

Corollaire: Tout angle est congru à lui-même.

III.5: Soient deux triangles ABC et A'B'C' tel que AB est congru à A'B' , AC est congru à A'C' , et l'angle BAC est congru à l'angle B'A'C' , alors le triangle ABC est congru au triangle A'B'C' .

IV. Continuité

IV.1: Axiome d'Archimède. Soient deux segments AB et CD tel que C est différent de D, il existe n points A₁,...,A_n de la droite contenant le segment AB, tels que A_j se situe entre A_j-1 et A_j+1 si 2 ≤ j < n - 1, A_jA_j+1 est congru à CD si 1≤ j <n - 1, A est confondu avec A₁ et B se situe entre A et A_n.

Ce groupe peut, ou non, être complété par un axiome impliquant la complétude de la géométrie.

IV.2: Axiome de Cantor. Si (A_n) et (B_n) sont deux suites infinies de points telles que le segment A_i+1B_i+1 est inclus dans le segment A_iB_i. Si pour tout segment CD congru à un segment de la droite contenant A et B, il existe i tel que le segment A_iB_i soit congru à un segment inclus dans CD, alors il existe un point appartenant à tous les segments A_iB_i. En d'autres termes : Toute suite de segments emboîtés dont la longueur tend vers 0 admet un point commun.

V. Parallèles

V.1: Soient une droite d et un point A non inclus dans d, alors il existe un plan contenant d et A. Ce plan contient une et une unique droite contenant A et ne contenant aucun point de d.

Commentaires

Dans l'article de 1899, Hilbert avait ajouté un 21eme axiome redondant : il était possible de le déduire des autres. Le mathématicien Eliakim Hastings Moore (1862 1932) démontra la redondance en 1902.

"Soient quatre points sur une droite, il est toujours possible de les nommer A, B, C, et D, tel que B est entre A et C et entre A et D. De sorte que, C se trouve entre A et D et aussi entre B et D."

Cette base axiomatique décrit l'espace euclidien de dimension trois. Il est relativement simple de transformer les hypothèses pour décrire un espace de dimension 2.

Cette axiomatique se formalise naturellement dans un calcul des prédicats à plusieurs types d'objets, les points, les droites, et les plans, une variante du calcul des prédicats ordinaire, où on préfère séparer syntaxiquement les objets de base du modèle plutôt que de les définir par des prédicats. Les axiomes de continuité ne sont pas des axiomes de la logique du premier ordre : ils requièrent la logique du second ordre (quantifications sur des ensembles d'objets de base). Tarski a donné une axiomatisation au premier ordre de la géométrie, qui repose de fait sur la notion de corps réel clos (et non sur le corps des réels), et qui est décidable et complète, à la différence de l'axiomatisation de Hilbert.

L'intérêt de l'approche de Hilbert est plus méthodologique que pédagogique ou appliquée. En effet, dès cette époque était déjà connue l'approche algébrique par des espaces vectoriels abstraits et des produits scalaires. Son article sur les fondements n'a donc une conséquence que secondaire en géométrie. En revanche, la démarche consistant à définir une approche axiomatique non redondante, consistante et si possible complète est avant-gardiste. L'article, durant le XX^e siècle, est d'une influence considérable sur l'approche axiomatique formelle en logique.

Sources

Liens internes

• Axiome d'Euclide : le cinquième postulat d'Euclide

Liens externes

• (fr) Les axiomes de Hilbert par Fabien Besnard, professeur de mathématiques, en lycée et à l'EPF
• (en) The Foundations of Geometry Texte original de David Hilbert
• (fr) La référence à l’espace et au temps dans le fondement des mathématiques par P. Cassou-Noguès CNRS UMR 8519
• (fr) Les 100 ans de la géométrie de Hilbert H. Languereau Mathématiques vivantes Bulletin IREM n° 66 2001

Références

• D Hilbert, Les fondements de la géométrie, Dunod, Paris, 1971 
• Gilbert Arsac, L'axiomatique de Hilbert et l'enseignement de la géométrie au Collège et au Lycée, Aleas, Lyon, octobre 1998, 125 p. (ISBN 2-84301-004-7) 
• M J Greenberg, Euclidiean and non-Euclidiean geometries, W.H. Freeman and Company 

• Portail de la géométrie
• Portail de la logique