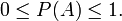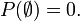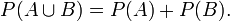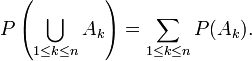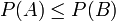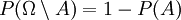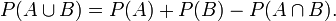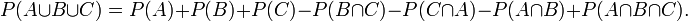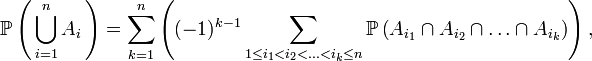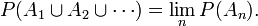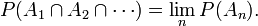Axiomes de Kolmogorov

Axiomes de Kolmogorov

Axiomes des probabilités

Dans la théorie des probabilités, une mesure de probabilité (ou plus brièvement probabilité) 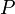\ P est une application qui à un évènement 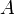\ A quelconque lié à l'expérience aléatoire 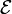\mathcal E associe un nombre réel (noté 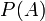\ P(A)) définie de telle manière qu'elle satisfasse les axiomes des probabilités ou axiomes de Kolmogorov, du nom d'Andrei Nikolaievitch Kolmogorov, mathématicien russe qui les a développés

Sommaire

Premier axiome

Pour tout évènement \ A :

0 \leq P(A) \leq 1.

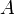C'est-à-dire que la probabilité d'un évènement est représentée par un nombre réel compris entre 0 et 1.

Deuxième axiome

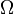\ \Omega désignant l'univers associé à l'expérience aléatoire considérée,

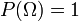\ P(\Omega) = 1,

C'est-à-dire que la probabilité de l'évènement certain, ou d'obtenir un quelconque résultat de l'univers, est égale à 1. Autrement dit, la probabilité de réaliser l'un ou l'autre des évènements élémentaires est égale à 1.

Troisième axiome

Toute suite d'évènements deux à deux disjoints (on dit aussi : deux à deux incompatibles), 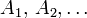A_1,\, A_2, \dots satisfait :

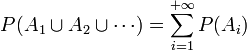P(A_1 \cup A_2 \cup \cdots) = \sum_{i = 1}^{+\infty} P(A_i).

C'est-à-dire que la probabilité d'un évènement qui est la réunion (dénombrable) disjointe d'évènements est égale à la somme des probabilités de ces évènements. Ceci s'appelle la σ-additivité, ou additivité dénombrable (si les évènements ne sont pas deux à deux disjoints, cette relation n'est plus vraie en général).

Conséquences

À partir des axiomes, se démontrent un certain nombre de propriétés utiles pour le calcul des probabilités, par exemple :

  • P(\emptyset)=0.
Démonstration

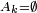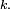Utilisons le 3ème axiome avec \scriptstyle\ A_k=\emptyset\ pour tout \scriptstyle\ k.\ On obtient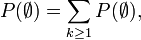

P(\emptyset)=\sum_{k\ge 1}P(\emptyset),

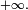relation qui n'est pas satisfaite si \scriptstyle\ P(\emptyset)\in]0,1],\ puisqu'alors le terme de droite vaut \scriptstyle\ +\infty.\ Donc il ne reste que 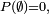\scriptstyle\ P(\emptyset)=0,\ qui d'ailleurs convient.

  • Si 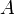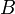\ A, \ B sont deux évènements incompatibles (ou disjoints), alors
P(A \cup B) = P(A) + P(B).
  • Plus généralement, si 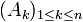\ (A_k)_{1\le k\le n} est une famille d'évènements 2 à 2 incompatibles, alors
P\left(\bigcup_{1\le k\le n} A_k\right) = \sum_{1\le k\le n}P(A_k).
Démonstration

Utilisons le 3ème axiome avec 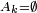\scriptstyle\ A_k=\emptyset\ pour tout 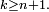\scriptstyle\ k\ge n+1.\ On obtient bien une suite d'évènements incompatibles 2 à 2 tels que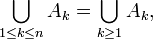

\bigcup_{1\le k\le n} A_k=\bigcup_{k\ge 1} A_k,

donc

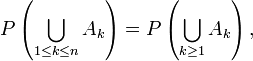
P\left(\bigcup_{1\le k\le n} A_k\right)=P\left(\bigcup_{k\ge 1} A_k\right),

mais en vertu du troisième axiome

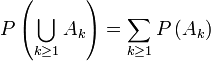
P\left(\bigcup_{k\ge 1} A_k\right)=\sum_{k\ge 1}P\left(A_k\right)

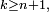
et finalement, puisque pour tout 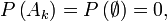\scriptstyle\ k\ge n+1,\ P\left(A_k\right)=P\left(\emptyset\right)=0,\ on obtient le résultat désiré.

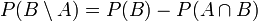  • P(B \setminus A) = P(B) - P(A \cap B);

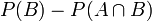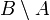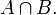
Cette relation signifie que la probabilité que B se réalise, mais pas A, est égale à la différence P(B) - P(A \cap B). Cette relation découle de ce que B est réunion disjointe de B \setminus A et de A \cap B.

  • En particulier, si 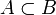A \subset B, alors
P(A) \leq P(B)

C'est la propriété de croissance de la probabilité. En effet, dans le cas particulier où 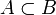A \subset B, la propriété précédente s'écrit

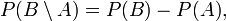P(B \setminus A) =P(B) - P(A),\ où le premier terme est clairement positif ou nul.
  • Dans le cas particulier où B = Ω, cela donne que, pour tout évènement \ A,
P(\Omega \setminus A) = 1 - P(A)

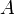Ceci signifie que la probabilité pour qu'un évènement ne se produise pas est égale à 1 moins la probabilité pour qu'il se réalise ; cette propriété s'utilise lorsqu'il est plus simple de déterminer la probabilité de l'évènement contraire que celle de l'évènement lui-même.

  • Pour tous évènements \ A, \ B,
P(A \cup B) = P(A) + P(B) - P(A \cap B).

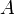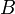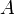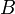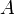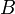Ceci signifie que la probabilité pour que l'un au moins des évènements A ou B se réalise est égale à la somme des probabilités pour que \ A se réalise, et pour que \ B se réalise, moins la probabilité pour que \ A et \ B se réalisent simultanément. De même,

P(A \cup B \cup C) = P(A) + P(B) + P(C) - P(B \cap C) - P(C \cap A) - P(A \cap B) + P(A \cap B \cap C).
\mathbb{P}\left(\,\bigcup_{i=1}^n A_i\,\right)=\sum_{k=1}^n \left((-1)^{k-1} \sum_{1\leq i_1<i_2<\ldots<i_k\leq n} \mathbb{P}\left(A_{i_1}\cap A_{i_2}\cap \ldots \cap A_{i_k}\right)\right),

qui donne la probabilité de la réunion de n ensembles non nécessairement disjoints.

Limites croissantes et décroissantes

  • Toute suite croissante d'évènements 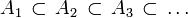A_1\,\subset\, A_2\,\subset\, A_3\,\subset\,\dots satisfait :
P(A_1 \cup A_2 \cup \cdots) = \lim_{n} P(A_n).

C'est-à-dire que la probabilité d'un évènement qui est la réunion (dénombrable) d'évènements croissants est égale à la limite des probabilités de ces évènements.

Démonstration

On pose

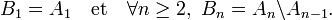
B_1=A_1\quad\text{et}\quad\forall n\ge 2, \ B_n=A_n\backslash A_{n-1}.

Alors les Bi sont disjoints et vérifient

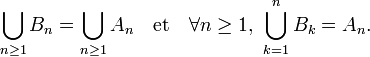
\bigcup_{n\ge 1}B_n=\bigcup_{n\ge 1}A_n\quad\text{et}\quad\forall n\ge 1, \ \bigcup_{k= 1}^nB_k=A_n.

Les propriétés de σ-additivité et d'additivité, respectivement, entrainent alors que

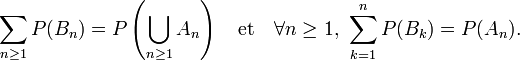
\sum_{n\ge 1}P(B_n)=P\left(\bigcup_{n\ge 1}A_n\right)\quad\text{et}\quad\forall n\ge 1, \ \sum_{k= 1}^nP(B_k)=P(A_n).

Alors 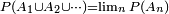\scriptstyle\ P(A_1 \cup A_2 \cup \cdots) = \lim_{n} P(A_n) n'est autre que la définition de la somme d'une série comme limite de ses sommes partielles.

  • Toute suite décroissante d'évènements 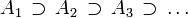A_1\,\supset\, A_2\,\supset\, A_3\,\supset\,\dots satisfait :
P(A_1 \cap A_2 \cap \cdots) = \lim_{n} P(A_n).

C'est-à-dire que la probabilité d'un évènement qui est l'intersection (dénombrable) d'évènements décroissants est égale à la limite des probabilités de ces évènements.

Formulation à partir de la théorie de la mesure

Article détaillé : Théorie de la mesure.

De manière équivalente, on définit plus simplement mais plus abstraitement ce qui précède par un triplet 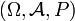(\Omega,\mathcal{A},P) représentant un espace de probabilités, ce qui permet d'utiliser directement les résultats de la théorie de la mesure et de l'intégration de Lebesgue.

Articles de mathématiques en rapport avec les probabilités ou les statistiques
  • Portail des probabilités et des statistiques Portail des probabilités et des statistiques
Ce document provient de « Axiomes des probabilit%C3%A9s ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Axiomes de Kolmogorov de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Axiomes Des Probabilités — Dans la théorie des probabilités, une mesure de probabilité (ou plus brièvement probabilité) est une application qui à un évènement quelconque lié à l expérience aléatoire associe un nombre réel (noté ) définie de telle manière qu elle satisfasse …   Wikipédia en Français

  • Axiomes des probabilites — Axiomes des probabilités Dans la théorie des probabilités, une mesure de probabilité (ou plus brièvement probabilité) est une application qui à un évènement quelconque lié à l expérience aléatoire associe un nombre réel (noté ) définie de telle… …   Wikipédia en Français

  • Axiomes des probabilités — Dans la théorie des probabilités, une mesure de probabilité (ou plus brièvement probabilité) est une application qui à un évènement A quelconque associe un nombre réel (noté ). Une mesure de probabilité doit satisfaire les axiomes des… …   Wikipédia en Français

  • Andreï Kolmogorov — Andreï Nikolaïevitch Kolmogorov Naissance 25 Avril 1903 Tambov (Empire russe) Décès 20 Octobre 1987 (84 ans) Moscou (Union soviétique) Nationalité …   Wikipédia en Français

  • Espace De Kolmogorov — Pour les articles homonymes, voir T0. En topologie et dans d autres branches des mathématiques, un espace de Kolmogorov (ou espace T0) est un espace topologique dans lequel tous les points peuvent être distingués du point de vue topologique. De… …   Wikipédia en Français

  • Espace de Kolmogorov — Pour les articles homonymes, voir T0. En topologie et dans d autres branches des mathématiques, un espace de Kolmogorov (ou espace T0) est un espace topologique dans lequel tous les points peuvent être distingués du point de vue topologique. De… …   Wikipédia en Français

  • Espace de kolmogorov — Pour les articles homonymes, voir T0. En topologie et dans d autres branches des mathématiques, un espace de Kolmogorov (ou espace T0) est un espace topologique dans lequel tous les points peuvent être distingués du point de vue topologique. De… …   Wikipédia en Français

  • Mesure de probabilité — Axiomes des probabilités Dans la théorie des probabilités, une mesure de probabilité (ou plus brièvement probabilité) est une application qui à un évènement quelconque lié à l expérience aléatoire associe un nombre réel (noté ) définie de telle… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”