- Théorème des milieux (mathématiques élémentaires)
-
Théorème des milieux
Le théorème des milieux est un cas particulier de la réciproque du théorème de Thalès.
Sommaire
Théorème direct
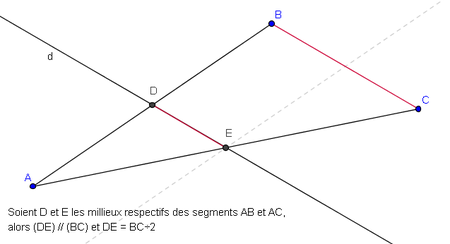
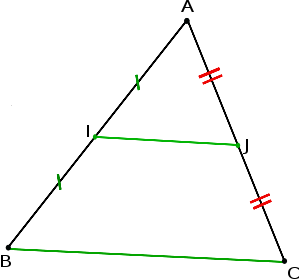
- Si une droite passe par les milieux de deux côtés d’un triangle, alors elle est parallèle au troisième côté.
- Si un segment a pour extrémités les milieux de deux côtés d'un triangle, alors la longueur de ce segment est égale à la moitié de la longueur du troisième côté.
- (Dans un triangle,le segment qui joint les milieux de deux côtés mesure la moitié du troisième côtés).
Voici les 2 théorémes de cette section mais il existe des théorèmes connexes
Formulation graphique
Ce théorème peut se présenter graphiquement de la manière suivante :
Formulation en français
- "Si une droite passe par les milieux de deux côtés d'un triangle alors elle est parallèle au troisième côté.
- La longueur du segment joignant les milieux de deux côtés d'un triangle est égale à la moitié de celle du troisième côté"
Démonstration
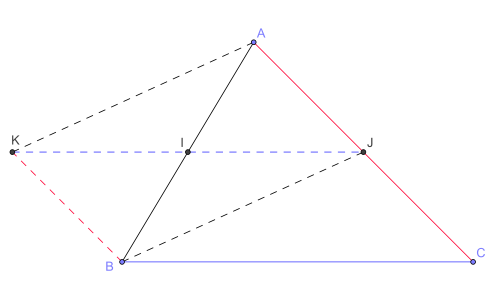
Sur la figure, (IJ) est la droite des milieux dans ABC qu’on veut prouver parallèle à (BC).
Soit K le symétrique de J par rapport à I, on a alors I milieu de [JK] et
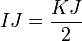 .
.Comme I est par hypothèse le milieu de [AB], les diagonales de AJBK se coupent en leur milieu commun I, donc AJBK est un parallélogramme.
Ses côtés [AJ] et [KB] sont parallèles et de même longueur, et il en est donc de même pour [JC] et [KB].KBCJ n’est pas croisé (B et C sont dans le même demi-plan par rapport à (KJ), B comme symétrique de A par rapport à I, C comme symétrique de A par rapport à J).
- Or si un quadrilatère non-croisé a deux côtés opposés parallèles et de même longueur alors c'est un parallélogramme.
Donc KBCJ est un parallélogramme.
Par les propriétés du parallélogramme, les côtés opposés [KJ] et [BC] sont parallèles, la droite (IJ) est donc parallèle à (BC).
Comme les côtés opposés sont égaux, de KJ = BC on déduit :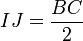 .
.Remarque : On évite la complication du quadrilatère croisé avec une preuve vectorielle :
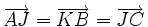
Théorème réciproque
C'est un cas particulier du théorème direct de Thalès.
Théorème : Si une droite passe par le milieu d'un des côtés d'un triangle et si elle est parallèle à un autre côté alors elle coupe le troisième côté en son milieu ( voir ci-dessous )
- Portail de la géométrie
Catégories : Géométrie du triangle | Théorème de géométrie | Mathématiques élémentaires
Wikimedia Foundation. 2010.