Théorème des milieux

Le théorème des milieux est un cas particulier de la réciproque du théorème de Thalès.

Théorème direct

Deux énoncés

Voici les deux théorèmes principaux, mais il existe des théorèmes connexes.

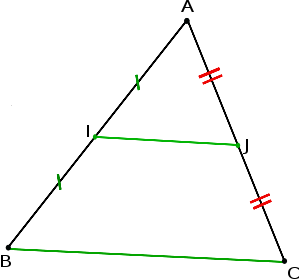
• Si une droite passe par les milieux de deux côtés d’un triangle, alors elle est parallèle au troisième côté.
• La longueur du segment ayant pour extrémités les milieux de deux côtés d'un triangle est égale à la moitié de celle du troisième côté.

Formulation graphique

Ce théorème peut se présenter graphiquement de la manière suivante :

Soient I et J les milieux respectifs des segments [AB] et [AC], alors (IJ) // (BC) et IJ = BC ÷ 2.

Démonstration en géométrie élémentaire

Le point auxiliaire K fait apparaître un parallélogramme.

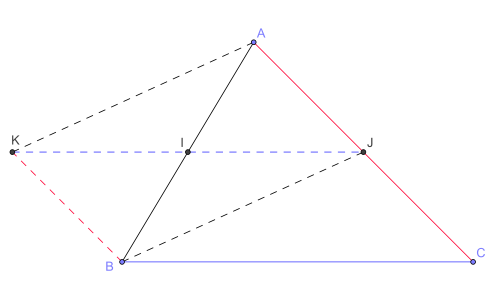
Cette propriété se démontre sans que soit connue la définition d'un vecteur. Sur la figure, (IJ) est la droite des milieux dans ABC qu’on veut prouver parallèle à (BC).

Soit K le symétrique de J par rapport à I, on a alors I milieu de [JK] et .

Comme I est par hypothèse le milieu de [AB], les diagonales de AJBK se coupent en leur milieu commun I, donc AJBK est un parallélogramme.
Ses côtés [AJ] et [KB] sont parallèles et de même longueur, et il en est donc de même pour [JC] et [KB].

KBCJ n’est pas croisé (B et C sont dans le même demi-plan par rapport à (KJ), B comme symétrique de A par rapport à I, C comme symétrique de A par rapport à J).

Or si un quadrilatère non croisé a deux côtés opposés parallèles et de même longueur alors c'est un parallélogramme.

Donc KBCJ est un parallélogramme.

Par les propriétés du parallélogramme, les côtés opposés [KJ] et [BC] sont parallèles, la droite (IJ) est donc parallèle à (BC).
Comme les côtés opposés sont égaux, de KJ = BC on déduit : .

Démonstration vectorielle

Lorsque la notion de vecteur est déjà connue - par exemple, dans le cas d'un espace affine euclidien associé à un espace vectoriel - il existe une démonstration vectorielle beaucoup plus courte.

Puisque I est milieu de (A,B) et J est milieu de (A,C), on a

d'où

Les vecteurs et sont colinéaires donc les droites (IJ) et (BC) sont parallèles.

La norme de est égale à la moitié de celle de , autrement dit la distance IJ est égale à BC ÷ 2.

Théorème réciproque

C'est un cas particulier du théorème direct de Thalès.

Il existe une démonstration de cette réciproque faisant intervenir uniquement des notions d'aire.

On suppose que la droite passe par le milieu I de côté [AB], qu'elle est parallèle au côté [BC] et qu'elle coupe le côté [AC] en un point J'.

Le triangle CBI a même sommet que le triangle CBA et a une base moitié donc

aire (CBI) = ¹⁄₂ aire (CBA).

Le segment [IJ'] est parallèle à la base [BC], donc, par cisaillement,

aire (CBI) = aire (CBJ').

L'aire du triangle BCJ' est donc la moitié de l'aire du triangle BCA et les points C, J' et A sont alignés donc

CJ' = ¹⁄₂ CA

Le point J' est donc égal au milieu J du segment [CA].

Alternativement, le théorème réciproque peut se déduire du théorème direct : avec les mêmes notations que ci-dessus, la droite (IJ') est – par hypothèse – parallèle à (BC), elle-même parallèle à (IJ) d'après le théorème direct. Ainsi, les deux droites (IJ') et (IJ) sont parallèles. Comme elles ont un point commun I, elles sont confondues, si bien que leur intersection avec (AC) est la même : J'=J.

Voir aussi

• Portail de la géométrie