Théorème des gendarmes

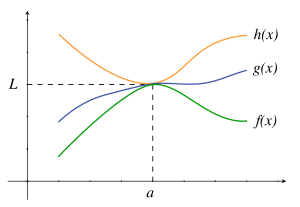
Deux fonctions f et h qui admettent la même limite L au point a et une fonction g prise en « étau » entre f et h dans le voisinage de a. Le théorème sandwich stipule donc que g admet L comme limite en a.

En analyse, le théorème des gendarmes (également appelé théorème d'encadrement, théorème du pincement, théorème de l'étau ou théorème du sandwich) est un théorème concernant la limite d'une fonction. Ce théorème stipule que si deux fonctions ( $f$ et $h$ ) admettent la même limite en un point ( $a$ ) et qu'une troisième fonction ( $g$ ) est prise en « étau » (ou « encadrée » ou « prise en sandwich ») entre $f$ et $h$ dans le voisinage de $a$ , alors $g$ admet la même limite en $a$ .

Le théorème des gendarmes est une technique très importante en calcul infinitésimal et en analyse. Il est généralement utilisé afin de déterminer la limite d'une fonction via la comparaison avec deux autres fonctions dont la limite est connue ou facilement calculable.

Énoncé

Soit $I$ un intervalle contenant le point $a$ . Soit $f$ , $g$ et $h$ trois fonctions réelles définies sur l'intervalle $I$ , sauf possiblement au point $a$ .

si pour tout $x$ de $I$ qui n'est pas égal à $a$ on a $f(x)\le g(x) \le h(x)$
et si $\lim_{x \to a}f(x) = \lim_{x \to a}h(x) = L$ ,
alors $\lim_{x \to a}g(x) = L$

Remarques

$a$ peut être situé à l'intérieur de l'intervalle $I$ ou à une de ses bornes (extrémités). En effet, dans ce dernier cas, on considérera la limite à gauche ou la limite à droite.
$a$ peut être fini ou infini. En effet, basé sur la remarque précédente, si, par exemple, $I = [0, +\infty [$ , nous pouvons utiliser la limite lorsque $x \to +\infty$ .

Origine du nom

Pour comprendre le nom familier du théorème, il faut assimiler les fonctions $f$ et $h$ à des gendarmes et $g$ à un délinquant. Ce dernier, encadré par les deux gendarmes, est obligé de les suivre jusqu'à la gendarmerie $L$ . En Italie, on l'appelle « théorème des carabiniers », « théorème de l'affrontement », ou encore « théorème du sandwich »...

Démonstration

La démonstration met directement en œuvre la notion de voisinage de $a$ et la définition de la limite.

Pour tout intervalle ouvert U contenant L,

Puisque $\lim_{x \to a}f(x) = L$ , il existe un voisinage V₁ de $a$ tel que

pour tout

x

de V₁, $f(x) \in U$

Puisque $\lim_{x \to a}h(x) = L$ , il existe un voisinage V₂ de $a$ tel que

pour tout x de V₂, $h(x) \in U$

Enfin, d'après la propriété d'encadrement, il existe un voisinage V₃ de $a$ tel que

pour tout x de V₃, $f(x) \le g(x) \le h(x)$

L'intersection de trois voisinages est un voisinage donc $V = V_1 \cap V_2 \cap V_3$ est un voisinage de $a$ et pour tout $x$ de V, on a

$f(x) \in U$
$h(x) \in U$
$f(x) \le g(x) \le h(x)$

d'où il vient que pour tout voisinage $U$ contenant $L$ , il existe un voisinage $V$ tel que $x\in V$ implique $g(x) \in U,$

ce qui prouve que $\lim_{x \to a}g(x) = L$

Exemple

Montrons que :

$\lim_{x \to +\infty} {\sin(x)\over x} = 0$

On a, pour tout réel x :

$-1 \le \sin(x) \le 1$

Donc, pour tout réel x strictement positif :

$-{1\over x} \le {\sin(x)\over x} \le {1\over x}$

Or :

$\lim_{x \to +\infty} -{1\over x} = 0$ et $\lim_{x \to +\infty} {1\over x} = 0$

Ainsi, d'après le théorème dit « des gendarmes » :

$\lim_{x \to +\infty} {\sin(x)\over x} = \lim_{x \to +\infty} -{1\over x} = \lim_{x \to +\infty} {1\over x} = 0$

Variantes

Des variantes de ce théorème existent pour des fonctions dont la limite est infinie, mais ce sont des théorèmes de comparaison distincts de celui des gendarmes (à donc utiliser en écrivant « d'après un théorème de comparaison »).

f

g

sont deux fonctions réelles définies sur un même intervalle

I

, telles que pour tout

x

I

dans un voisinage de

a

$f(x)\le g(x)$ et $\lim_{x \to a}f(x) = +\infty$ (a fini ou non), alors on a aussi : $\lim_{x \to a}g(x) = + \infty$

f

g

sont deux fonctions réelles définies sur un même intervalle

I

, telles que pour tout

x

I

dans un voisinage de

a

$f(x)\le g(x)$ et $\lim_{x \to a}g(x) = -\infty$ (a fini ou non), alors on a aussi : $\lim_{x \to a}f(x) = - \infty$

f

g

sont deux fonctions réelles définies sur un même intervalle

I

, telles que pour tout

x

I

dans un voisinage de

a

$0 \le f(x)\le g(x)$ et $\lim_{x \to a}g(x) = 0$ (a fini ou non), alors on a aussi : $\lim_{x \to a}f(x) = 0$

Enfin des théorèmes analogues existent pour des limites de suites

Si u, v et w sont trois suites réelles, telles que pour tout n > N

$u_n\le v_n \le w_n$ et $\lim_{n \to +\infty}u_n = \lim_{n \to +\infty}w_n = L$ , alors on a aussi : $\lim_{n \to +\infty}v_n = L$

avec les variantes pour les limites infinies.

Les démonstrations de toutes ces variantes sont analogues à celle développée plus haut.

Regardez d'autres dictionnaires:

Theoreme des gendarmes — Théorème des gendarmes Deux fonctions f et h qui admettent la même limite L au point a et une fonction g prise en « étau » entre f et h dans le voisinage de a. Le théorème sandwich stipule donc que g admet L comme limite en a. En… … Wikipédia en Français
Théorème des Croissances Comparées — Cet article fait partie de la série Mathématiques élémentaires Algèbre Logique Arithmétique Probabilités … Wikipédia en Français
Théorème des croissances comparées — Le théorème des croissances comparées est constitué de quelques résultats de limites de fonctions qui seraient qualifiées de formes indéterminées par la méthode usuelle. Sommaire 1 Énoncé des résultats classiques 1.1 Démonstrations 2 … Wikipédia en Français
Theoreme sandwich — Théorème des gendarmes Deux fonctions f et h qui admettent la même limite L au point a et une fonction g prise en « étau » entre f et h dans le voisinage de a. Le théorème sandwich stipule donc que g admet L comme limite en a. En… … Wikipédia en Français
Théorème d'encadrement — Théorème des gendarmes Deux fonctions f et h qui admettent la même limite L au point a et une fonction g prise en « étau » entre f et h dans le voisinage de a. Le théorème sandwich stipule donc que g admet L comme limite en a. En… … Wikipédia en Français
Théorème de l'étau — Théorème des gendarmes Deux fonctions f et h qui admettent la même limite L au point a et une fonction g prise en « étau » entre f et h dans le voisinage de a. Le théorème sandwich stipule donc que g admet L comme limite en a. En… … Wikipédia en Français
Théorème sandwich — Théorème des gendarmes Deux fonctions f et h qui admettent la même limite L au point a et une fonction g prise en « étau » entre f et h dans le voisinage de a. Le théorème sandwich stipule donc que g admet L comme limite en a. En… … Wikipédia en Français
Théorème du sandwich (variante) — Ceci est une version alternative du théorème du sandwich qui concerne les dérivées (ou différentielles) de fonctions, si vous cherchiez un théorème sur un passage à la limite référez vous plutôt à l article théorème des gendarmes. Énoncé (cas d… … Wikipédia en Français
Théorème du sandwich — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Ce théorème peut correspondre au: théorème des gendarmes, un théorème de passage à la limite. théorème du sandwich (variante), un théorème sur les… … Wikipédia en Français
Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème des gendarmes

Sommaire

Énoncé

Remarques

Origine du nom

Démonstration

Exemple

Variantes

Articles connexes

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Théorème des gendarmes

Sommaire

Énoncé

Remarques

Origine du nom

Démonstration

Exemple

Variantes

Articles connexes

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link