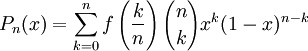Théorème de weierstrass

Le théorème d'approximation de Weierstrass affirme que toute fonction continue définie sur un compact peut être approchée aussi près que l'on veut par une fonction polynomiale. Parce que les fonctions polynômes sont les fonctions les plus simples, et que les ordinateurs peuvent directement évaluer les polynômes, ce théorème a à la fois un intérêt pratique et théorique. Il a été énoncé par Karl Weierstrass en 1885. Marshall H. Stone a considérablement généralisé le théorème et simplifié la démonstration ; c'est cette amélioration qui s'appelle le théorème de Stone-Weierstrass.

Sommaire 1 Théorème d'approximation de Weierstrass 2 Version trigonométrique 3 Formes plus générales : théorème de Stone-Weierstrass 3.1 Le théorème de Stone-Weierstrass, version algébrique 3.2 Applications 3.3 Le théorème de Stone-Weierstrass, version treillis 4 Voir aussi

Théorème d'approximation de Weierstrass

Supposons que f soit une fonction continue définie sur l'intervalle [a,b] à valeurs réelles. Pour tout ε>0, il existe une fonction polynôme p à coefficients réels telle que pour tout x dans [a,b], nous ayons |f(x) - p(x)| < ε.

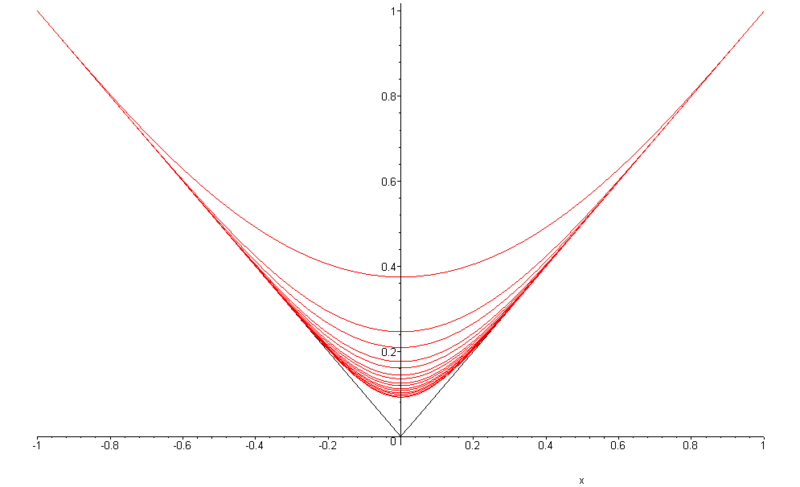
Cette propriété peut également s'exprimer sous la forme suivante : si f est une fonction continue sur [a,b], il existe une suite (P_n) de polynômes convergeant uniformément vers f sur [a,b]. Ci-dessous par exemple, la suite de polynômes converge vers la valeur absolue sur l'intervalle [-1,1].

En se ramenant par changement de variables à l'intervalle [0,1], Bernstein en a donné une démonstration constructive en prouvant qu'on pouvait prendre :

Les 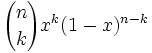sont les polynômes de Bernstein.

L'ensemble C([a,b]) des fonctions continues sur [a,b] à valeurs réelles, muni de la norme infinie , est une algèbre de Banach, (i.e. une algèbre associative et un espace de Banach telle que pour toutes f et g, ||fg|| ≤ ||f|| ||g||). L'ensemble des fonctions polynomiales forme une sous-algèbre de C([a,b]), et le théorème d'approximation de Weierstrass dit que cette sous-algèbre est dense dans C([a,b]).

Version trigonométrique

Pour toute fonction f continue T-périodique, il existe une suite (T_n) de polynômes trigonométriques qui convergent uniformément vers f.

Le théorème de Fejér, issu de la théorie des séries de Fourier, donne un exemple concret d'une telle suite.

Formes plus générales : théorème de Stone-Weierstrass

Le théorème de Stone-Weierstrass, version algébrique

Le théorème d'approximation se généralise dans deux directions : à la place de l'intervalle compact [a,b], un espace séparé ou espace de Hausdorff compact arbitraire X peut être considéré, et à la place de l'algèbre des fonctions polynômes, une approximation avec des éléments d'autres sous-algèbres de C(X) peut être envisagée. La propriété cruciale, que la sous-algèbre doit vérifier, est qu'elle sépare les points : on dit qu'un sous-ensemble A de C(X) sépare les points si pour tout couple de points différents x et y de X et tout couple de nombres réels a et b il existe une fonction p de A telle que p(x) = a et p(y) = b. Formellement le théorème s'écrit :

si X est un espace de Hausdorff compact ayant au moins deux éléments, et si A est une sous-algèbre de l'algèbre de Banach C(X) qui sépare les points et contient une fonction constante non nulle, alors A est dense dans C(X).

Cela généralise le théorème de Weierstrass puisque les polynômes sur [a,b] forment une sous-algèbre de C[a,b] qui sépare les points.

Remarquons que le théorème précédent reste aussi vrai si nous remplaçons l'assertion que A sépare les points avec la légèrement plus faible assertion que pour tout couple de points distincts x et y de X, il existe une fonction p dans A telle que p(x) soit distinct de p(y).

On peut aussi remplacer le corps des nombres réels par le corps des nombres complexes. Dans ce cas, il faut ajouter l'hypothèse supplémentaire que A soit auto-adjointe, c'est-à-dire que .

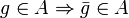Applications

Le théorème de Stone-Weierstrass peut être utilisé pour démontrer les deux propositions suivantes :

• si f est fonction continue à valeurs réelles définie sur le pavé [a,b] x [c,d] et si ε est réel strictement positif, alors il existe une fonction polynomiale p à deux variables telle que pour tous x dans [a,b] et y dans [c,d], |f(x,y) - p(x,y)| < ε.
• si X et Y sont deux espaces de Hausdorff compacts et si 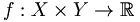est une fonction continue, alors pour tout ε>0 il existe n>0 et des fonctions continues f₁, f₂, ..., f_n sur X et des fonctions continues g₁, g₂, ..., g_n sur Y telles que ||f - ∑f_ig_i|| < ε

Le théorème de Stone-Weierstrass, version treillis

Soit X un espace de Hausdorff compact. Un sous-ensemble L de C(X) est appelé un treillis de C(X) si pour deux éléments quelconques f, g de L, les fonctions max(f,g) et min(f,g) appartiennent aussi à L. La version treillis du théorème de Stone-Weierstrass affirme que :

si X est un espace de Hausdorff compact avec au moins deux points et si L est un treillis de C(X) qui sépare les points, alors L est dense dans C(X).

Voir aussi

• Théorème de Chudnovsky
• Approximation de Bernstein

• Portail des mathématiques