- Théorème de plancherel
-
Théorème de Plancherel
Le théorème de Plancherel permet d'étendre la transformation de Fourier aux fonctions de carré sommable. Il fut démontré par le mathématicien Michel Plancherel[1].
Soit
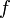 une fonction de carré sommable sur
une fonction de carré sommable sur  et soit A>0. On peut définir la transformée de Fourier de la fonction tronquée à [-A,A] :
et soit A>0. On peut définir la transformée de Fourier de la fonction tronquée à [-A,A] :Alors lorsque A tend vers l'infini, les fonctions
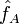 convergent en moyenne quadratique (c'est-à-dire pour la norme ||.||2) vers une fonction qu'on note
convergent en moyenne quadratique (c'est-à-dire pour la norme ||.||2) vers une fonction qu'on note 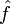 et que l'on appelle transformée de Fourier (ou de Fourier-Plancherel) de
et que l'on appelle transformée de Fourier (ou de Fourier-Plancherel) de 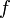 .
.En outre la formule d'inversion de Fourier est vérifiée : la fonction
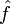 est elle-même de carré sommable et
est elle-même de carré sommable etAinsi la transformation de Fourier-Plancherel définit un automorphisme de l'espace L2, qui est qui plus est une isométrie
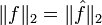
Cette définition est compatible avec la définition habituelle de la transformée de Fourier des fonctions intégrables.
Le théorème de Plancherel se généralise dans le cas où la transformée de Fourier est définie sur de nombreux groupes, on peut citer les groupes abéliens localement compacts (cf Dualité de Pontryagin) ou encore plus simplement les groupes abéliens finis (cf Analyse harmonique sur un groupe abélien fini).
Références
- ↑ Plancherel, Michel (1910) "Contribution a l'etude de la representation d'une fonction arbitraire par les integrales définies," Rendiconti del Circolo Matematico di Palermo, vol. 30, pages 298-335
- Portail des mathématiques
Catégories : Analyse harmonique | Mécanique ondulatoire | Spectroscopie | Théorie de l'intégration | Théorie de Fourier | Théorème de mathématiques | Transformée
Wikimedia Foundation. 2010.

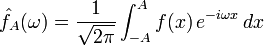
![f = \underset{A \mapsto +\infty}{\lim\limits_{\|\;\|_2}} \left[ \frac1{\sqrt{2\pi}}\, \int_{-A}^{A} \hat{f}(w)\, e^{iwx}\, dw\right]](/pictures/frwiki/102/fc6adf0dd6ccb638b7a18ea6dde78aba.png)