Théorème de Millman

Théorème de Millman

Le théorème de Millman est une forme particulière de la loi des nœuds exprimée en termes de potentiel. Il est ainsi nommé en l'honneur de l'électronicien américain Jacob Millman.

Sommaire

Énoncé

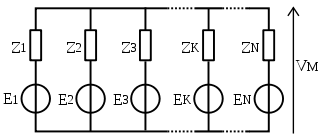
Illustration du théorème de Millman

Dans un réseau électrique de branches en parallèle, comprenant chacune un générateur de tension parfait en série avec un élément linéaire, la tension aux bornes des branches est égale à la somme des forces électromotrices respectivement multipliées par l'admittance de la branche, le tout divisé par la somme des admittances.

V_m=\frac{\displaystyle\sum_{k=1}^N E_k.Y_k}{\displaystyle\sum_{k=1}^N Y_k}=\frac{\displaystyle\sum_{k=1}^N \frac{E_k}{Z_k}}{\displaystyle\sum_{k=1}^N \frac{1}{Z_k}}

Dans le cas particulier d'un réseau électrique composé de résistances :

V_m=\frac{\displaystyle\sum_{k=1}^N E_k.G_k}{\displaystyle\sum_{k=1}^N G_k}=\frac{\displaystyle\sum_{k=1}^N \frac{E_k}{R_k}}{\displaystyle\sum_{k=1}^N \frac{1}{R_k}}

On peut aussi le généraliser avec des générateurs de courants. S'il y a, toujours en parallèle, des courants Ik connus injectés vers le même point M, alors on peut écrire :

V_m=\frac{\displaystyle\sum_{k=1}^N E_k.G_k+\sum_{k=1}^P I_k}{\displaystyle\sum_{k=1}^N G_k}=\frac{\displaystyle\sum_{k=1}^N \frac{E_k}{R_k}+\sum_{k=1}^P I_k}{\displaystyle\sum_{k=1}^N \frac{1}{R_k}}


Avec G, la conductance. On remarque que la présence de générateurs de courants ne modifie pas le dénominateur.

Démonstration

On considère le schéma ci-dessus.

Comme les branches (Zk ; Ek) sont en parallèle, on travaille avec les admittances Y_{k}=\frac{1}{Z_{k}}. Pour chaque branche (source de tension et impédance), on obtient, d'après la loi d'ohm : I_{k}=Y_{k} \times (E_{k}-V_{m}) (chaque courant est ainsi orienté vers le haut ; vers le point M)

Ensuite, d'après la loi des nœuds, on a : \sum_{k=1}^N I_{k}=0

Si on généralise avec des générateurs Ig de courants, on débute le même calcul ainsi : \sum_{k=1}^N I_{k}+\sum_{k=1}^P Ig_{k}=0

soit :

\sum_{k=1}^N Y_{k} \times (E_{k}-V_{m})+\sum_{k=1}^P Ig_{k}=0

en développant :

\sum_{k=1}^N Y_{k} \times V_{m} = \sum_{k=1}^N Y_{k} \times E_{k}+\sum_{k=1}^P Ig_{k}

d'où :

V_{m} = \frac{\displaystyle \sum_{k=1}^N E_{k} . Y_{k} + \sum_{k=1}^P Ig_{k}}{\displaystyle\sum_{k=1}^N Y_{k}}=\frac{\displaystyle\sum_{k=1}^N \frac{E_k}{Z_k} + \sum_{k=1}^P Ig_{k}}{\displaystyle\sum_{k=1}^N \frac{1}{Z_k}}
 

Exemple

Exemple d'application du théorème de Millman
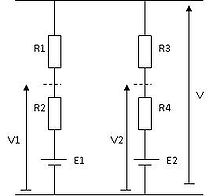
  • Sur la figure ci-contre, la tension Vab (ou Vm ), a été calculée en suivant la formule du théorème de Millman:
V_{ab}=\frac{\dfrac{V_1}{R_1}+\dfrac{V_2}{R_2}+\dfrac{V_3}{R_3}}{\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}} =\frac{\dfrac{10}{5}+\dfrac{0}{8}+\dfrac{-12}{3}}{\dfrac{1}{5}+\dfrac{1}{8}+\dfrac{1}{3}} = -3V
  • Le signe négatif signifie que le point a est négatif par rapport à la masse commune.

Autre exemple: Il n'est pas nécessaire que les sources de tension soient parfaites, celles-ci peuvent inclure des résistances même de forte valeur.

générateurs réels
V =\frac{\dfrac{E_1}{R_1+R_2}+\dfrac{E_2}{R_3+R_4}}{\dfrac{1}{R_1+R_2}+\dfrac{1}{R_3+R_4}}


V =\frac{\dfrac{V_1}{R_1}+\dfrac{V_2}{R_3}}{\dfrac{1}{R_1}+\dfrac{1}{R_3}}

Applications

Ce théorème s'utilise avantageusement si Vm est nulle (par exemple, la tension différentielle d'un AOP en régime linéaire), le dénominateur n'a pas besoin alors d'être formulé.

Voir aussi

Articles connexes


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de Millman de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Theoreme de Millman — Théorème de Millman Le théorème de Millman est une forme particulière de la loi des nœuds exprimée en termes de potentiel. Il est ainsi nommé en l honneur de l électronicien américain Jacob Millman. Sommaire 1 Énonciation 2 Exemple 3 Applications …   Wikipédia en Français

  • Théorème de millman — Le théorème de Millman est une forme particulière de la loi des nœuds exprimée en termes de potentiel. Il est ainsi nommé en l honneur de l électronicien américain Jacob Millman. Sommaire 1 Énonciation 2 Exemple 3 Applications …   Wikipédia en Français

  • Millman — est un patronyme qui peut désigner : Dan Millman, sportif et écrivain américain. Jacob Millman (1911 1991), électronicien américain, auteur du théorème de Millman. Peter Millman (1906 1990), astronome canadien qui a donné son nom à l… …   Wikipédia en Français

  • Theoreme de Thevenin — Théorème de Thévenin Le théorème de Thévenin a été initialement découvert par le scientifique allemand Hermann von Helmholtz en 1853, puis en 1883 par l ingénieur télégraphe français Léon Charles Thévenin. Ce théorème est une propriété… …   Wikipédia en Français

  • Théorème de thévenin — Le théorème de Thévenin a été initialement découvert par le scientifique allemand Hermann von Helmholtz en 1853, puis en 1883 par l ingénieur télégraphe français Léon Charles Thévenin. Ce théorème est une propriété électronique qui se déduit… …   Wikipédia en Français

  • Theoreme de Norton — Théorème de Norton Le Théorème de Norton pour les réseaux électriques établit que tout circuit linéaire est équivalent à une source de courant idéale I, en parallèle avec une simple résistance R. Le théorème s applique à toutes les impédances,… …   Wikipédia en Français

  • Théorème de norton — Le Théorème de Norton pour les réseaux électriques établit que tout circuit linéaire est équivalent à une source de courant idéale I, en parallèle avec une simple résistance R. Le théorème s applique à toutes les impédances, pas uniquement aux… …   Wikipédia en Français

  • Théorème de Thévenin — Le théorème de Thévenin a été initialement découvert par le scientifique allemand Hermann von Helmholtz en 1853, puis en 1883 par l ingénieur télégraphe français Léon Charles Thévenin. Ce théorème est une propriété électronique qui se déduit… …   Wikipédia en Français

  • Théorème de Norton — Le Théorème de Norton pour les réseaux électriques établit que tout circuit linéaire est équivalent à une source de courant idéale I, en parallèle avec une simple résistance R. Le théorème s applique à toutes les impédances, pas uniquement aux… …   Wikipédia en Français

  • Théorème de superposition — Principe de superposition On dit qu un système est linéaire ou relève du principe de superposition si à la somme de deux excitations correspond la somme des deux réponses correspondantes. Plus précisément, les excitations étant notées f (par… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”