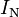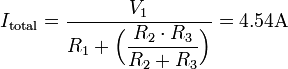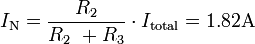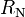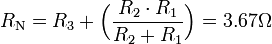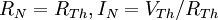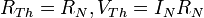Théorème de norton

Théorème de norton

Théorème de Norton

Le Théorème de Norton pour les réseaux électriques établit que tout circuit linéaire est équivalent à une source de courant idéale I, en parallèle avec une simple résistance R. Le théorème s'applique à toutes les impédances, pas uniquement aux résistances. L'énoncé de ce théorème a été publié en 1926 par l'ingénieur Edward Lawry Norton (1898-1983).

Communément :

  • Le courant de Norton est le courant entre les bornes de la charge lorsque celle-ci est court-circuitée, d'où Ic = I (court-circuit)
  • La résistance de Norton est celle mesurée entre les bornes de la charge lorsque toutes les sources sont rendues inactives en court-circuitant les sources de tension et en débranchant les sources de courant.

Sommaire

Exemple

Démonstration du théorème de Norton


  • En (a): Circuit originel.


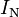
  • En (b): Court-circuit entre les bornes a et b pour trouver le courant Norton I_\mathrm{N} \


On calcul d'abord le courant total délivré par la source de tension;
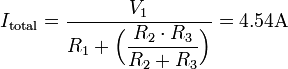
I_\mathrm{total} = {V_\mathrm{1} \over R_\mathrm{1} + \Bigl( \dfrac {R_\mathrm{2} \cdot R_\mathrm{3}}{R_\mathrm{2} + R_\mathrm{3}} \Bigr)} = 4.54 \mathrm{A}


On trouve ensuite le Courant de Norton par la formule du diviseur de courant;
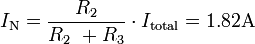
I_\mathrm{N} = {R_\mathrm{2} \over R_\mathrm{2}\ + R_\mathrm{3}} \cdot I_\mathrm{total} = 1.82 \mathrm{A}


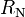
  • En (c): Court-circuit aux bornes de la source de tension et circuit ouvert entre a et b pour trouver la résistance de Norton R_\mathrm{N} \
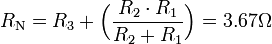
R_\mathrm{N} = R_\mathrm{3} + \Bigl( \dfrac {R_\mathrm{2} \cdot R_\mathrm{1}}{R_\mathrm{2} + R_\mathrm{1}} \Bigr) = 3.67 \Omega


  • En (d): Circuit équivalent de Norton

Conversion entre un circuit de Norton et de Thévenin

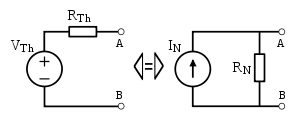
Circuit de Thévenin (à gauche) et circuit de Norton (à droite).

On passe directement d'un circuit de Norton à un circuit de Thévenin et inversement, à l'aide des formules suivantes:

  • De Thévenin à Norton;
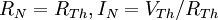
R_{N} = R_{Th}, I_{N} = V_{Th} / R_{Th} \!
  • De Norton à Thévenin;
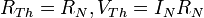
R_{Th} = R_{N} , V_{Th} = I_{N} R_{N} \!

Voir aussi

Lien externe

Sur les autres projets Wikimedia :

  • Portail de la physique Portail de la physique
  • Portail de l’électricité et de l’électronique Portail de l’électricité et de l’électronique
Ce document provient de « Th%C3%A9or%C3%A8me de Norton ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de norton de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Theoreme de Norton — Théorème de Norton Le Théorème de Norton pour les réseaux électriques établit que tout circuit linéaire est équivalent à une source de courant idéale I, en parallèle avec une simple résistance R. Le théorème s applique à toutes les impédances,… …   Wikipédia en Français

  • Théorème de Norton — Le Théorème de Norton pour les réseaux électriques établit que tout circuit linéaire est équivalent à une source de courant idéale I, en parallèle avec une simple résistance R. Le théorème s applique à toutes les impédances, pas uniquement aux… …   Wikipédia en Français

  • Theoreme de Thevenin — Théorème de Thévenin Le théorème de Thévenin a été initialement découvert par le scientifique allemand Hermann von Helmholtz en 1853, puis en 1883 par l ingénieur télégraphe français Léon Charles Thévenin. Ce théorème est une propriété… …   Wikipédia en Français

  • Théorème de thévenin — Le théorème de Thévenin a été initialement découvert par le scientifique allemand Hermann von Helmholtz en 1853, puis en 1883 par l ingénieur télégraphe français Léon Charles Thévenin. Ce théorème est une propriété électronique qui se déduit… …   Wikipédia en Français

  • Theoreme de reciprocite — Théorème de réciprocité Le principe de réciprocité, que l on retrouve également dans d autres domaines de la physique, s exprime dans celui de l électricité grâce à une relation générale entre les courants et les tensions observés aux interfaces… …   Wikipédia en Français

  • Theoreme de Millman — Théorème de Millman Le théorème de Millman est une forme particulière de la loi des nœuds exprimée en termes de potentiel. Il est ainsi nommé en l honneur de l électronicien américain Jacob Millman. Sommaire 1 Énonciation 2 Exemple 3 Applications …   Wikipédia en Français

  • Theoreme de Tellegen — Théorème de Tellegen En électricité, le Théorème de Tellegen est une conséquence directe des lois de Kirchhoff qui traduit en particulier la conservation de l énergie dans un circuit électrique isolé. Ce théorème doit son nom à Bernard Tellegen,… …   Wikipédia en Français

  • Théorème de millman — Le théorème de Millman est une forme particulière de la loi des nœuds exprimée en termes de potentiel. Il est ainsi nommé en l honneur de l électronicien américain Jacob Millman. Sommaire 1 Énonciation 2 Exemple 3 Applications …   Wikipédia en Français

  • Théorème de tellegen — En électricité, le Théorème de Tellegen est une conséquence directe des lois de Kirchhoff qui traduit en particulier la conservation de l énergie dans un circuit électrique isolé. Ce théorème doit son nom à Bernard Tellegen, un chercheur… …   Wikipédia en Français

  • Théorème de Thévenin — Le théorème de Thévenin a été initialement découvert par le scientifique allemand Hermann von Helmholtz en 1853, puis en 1883 par l ingénieur télégraphe français Léon Charles Thévenin. Ce théorème est une propriété électronique qui se déduit… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”