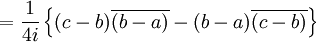Théorème Bonaparte

Théorème Bonaparte

Théorème de Napoléon

Figure du théorème de Napoléon

Le théorème de Napoléon est un théorème de géométrie portant sur le triangle équilatéral.

Bien qu'il soit traditionnellement attribué à Napoléon Bonaparte (d'où le nom du théorème) qui l’aurait énoncé pour la première fois en 1787[réf. nécessaire], il n'y a pas de preuve tangible qu'il soit effectivement l'auteur du théorème. La légende raconte qu'à la présentation du théorème devant l'Académie des sciences en 1797 au retour de la campagne d'Italie, Lagrange aurait dit à Napoléon : "Nous attendions tout de vous, mon Général, mais pas une leçon de géométrie."[1],[2].

Certaines sources[3],[4] précisent que la plus ancienne trace ne remonte qu'à la publication intitulée The Ladies Diary en 1825 par le Dr W. Rutherford, soit quatre ans après la mort de l'empereur.

Sommaire

Énoncé

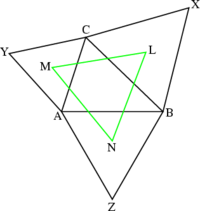
Théorème de Napoléon — Si nous construisons trois triangles équilatéraux à partir des côtés d'un triangle quelconque, tous à l'extérieur ou tous à l'intérieur, les centres de ces triangles équilatéraux forment eux-mêmes un triangle équilatéral.

Par « extérieur », il faut par exemple entendre qu'avec les notations de notre figure et un repère orienté, les triangles ABC et ABZ sont de sens opposés (ici ABC est dans le sens trigonométrique et ABZ dans le sens anti-trigonométrique), idem pour les deux autres. Dans le cas « intérieur », ils seraient de même sens.

Démonstration

Avec les nombres complexes

On notera 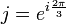j = e^{i\frac{2\pi}{3}} (notation usuelle) et on utilisera les notations de la figure.

On munit le plan complexe d'un repère orthonormé direct. Soient a, b, c, l, m et n les affixes respectives des points A, B, C, L, M et N dans ce repère.

Par construction, A est l'image de B par la rotation de centre N et d'angle 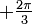\textstyle{+\frac{2\pi}{3}}, ce qui se traduit par :

(a − n) = j(b − n)

De même :

(b − l) = j(c − l)
(c − m) = j(a − m)

On en déduit :

(1 − j)n = a − jb
(1 − j)l = b − jc
(1 − j)m = c − ja

Comme 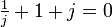\textstyle{\frac{1}{j}+1+j = 0} et j3 = 1, alors :

(1 − j)(m − n) = ( − 1 − j)a + jb + c

= j2a + j4b + j3c
= − j2[ − a + (1 + j)b − jc]
= − j2[(b − jc) − (a − jb)]
= − j2(1 − j)(l − n)

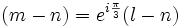En divisant par (1 − j) on obtient (m − n) = − j2(l − n) ou encore (m-n) = e^{i\frac{\pi}{3}}(l-n).

M est l'image de L par la rotation de centre N et d'angle 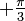\textstyle{+\frac{\pi}{3}} donc NLM est un triangle équilatéral direct.

Remarque : Cette démonstration reste valable dans le cas des triangles « intérieurs » en changeant quelques signes.

Lemmes

Lemme 1 — Les centres de gravité du triangle de départ ABC et du triangle final LMN sont coïncidents.

Ce lemme peut être facilement démontré en reprenant les notations de la démonstration avec les nombres complexes :

(1 − j)(n + l + m) = a − jb + b − jc + c − ja

= (1 − j)(a + b + c)

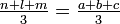
d'où l'égalité pour les affixes des barycentres \tfrac{n+l+m}{3} = \tfrac{a+b+c}{3}

Lemme 2 — La valeur absolue de la différence entre l'aire du triangle final "extérieur" LMN et l'aire du triangle final "intérieur" L1M1N1 est égale à l'aire du triangle de départ ABC.

Reprenons les notations précédentes, pour le triangle « intérieur » ; on obtient alors :

(1 − j)n1 = b − ja
(1 − j)l1 = c − jb
(1 − j)m1 = a − jc

et sachant que l'aire d'un triangle équilatéral de côté a peut être obtenu par : 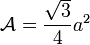\mathcal{A} = \frac{\sqrt{3}}{4}a^2 et que 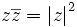z \overline{z} = \left|z\right|^2, calculons la différence :

\mathcal{A} = \frac{\sqrt{3}}{4}\left[(l-n)\overline{(l-n)} - (l_1-n_1)\overline{(l_1-n_1)}\right]

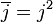
= \frac{\sqrt{3}}{4} \frac{1}{(1-j)\overline{(1-j)}} \left\{\left[(b-a)-j(c-b)\right]\left[\overline{(b-a)}-j^2\overline{(c-b)}\right]-\left[(c-b)-j(b-a)\right]\left[\overline{(c-b)}-j^2\overline{(b-a)}\right]\right\} car \overline{j} = j^2
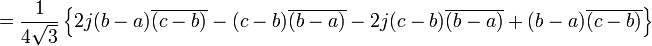= \frac{1}{4\sqrt{3}} \left\{2j(b-a)\overline{(c-b)}-(c-b)\overline{(b-a)}-2j(c-b)\overline{(b-a)}+(b-a)\overline{(c-b)}\right\} en développant et en sachant que j2 = − 1 − j

Comme 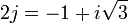2j = -1+i\sqrt{3} il vient :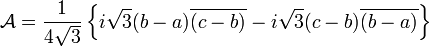

\mathcal{A} = \frac{1}{4\sqrt{3}} \left\{i\sqrt{3}(b-a)\overline{(c-b)}-i\sqrt{3}(c-b)\overline{(b-a)}\right\}

= \frac{1}{4i} \left\{(c-b)\overline{(b-a)}-(b-a)\overline{(c-b)}\right\}

Le résultat précédent est bien l'aire (algébrique) du triangle dont les affixes des sommets sont a, b et c.

Voir aussi

Références

  1. ↑ Rapporté par Henri Poincaré, voir Pages du Laboratoire Jean Kuntzmann, Grenoble.
  2. ↑ BibMath, Théorème de Napoléon.
  3. ↑ Schmidt, F. "200 Jahre französische Revolution--Problem und Satz von Napoleon." Didaktik der Mathematik 19, 15-29, 1990.
  4. ↑ Wentzel, J. E. "Converses of Napoleon's Theorem." Amer. Math. Monthly 99, 339-351, 1992.

Liens externes

  • Portail de la géométrie Portail de la géométrie
  • Portail du Premier Empire Portail du Premier Empire
Ce document provient de « Th%C3%A9or%C3%A8me de Napol%C3%A9on ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème Bonaparte de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Theoreme de Napoleon — Théorème de Napoléon Figure du théorème de Napoléon Le théorème de Napoléon est un théorème de géométrie portant sur le triangle équilatéral. Bien qu il soit traditionnellement attribué à Napoléon Bonaparte (d où le nom du théorème) qui l’aurait… …   Wikipédia en Français

  • Théorème de napoléon — Figure du théorème de Napoléon Le théorème de Napoléon est un théorème de géométrie portant sur le triangle équilatéral. Bien qu il soit traditionnellement attribué à Napoléon Bonaparte (d où le nom du théorème) qui l’aurait énoncé pour la… …   Wikipédia en Français

  • Théorème de Napoléon — Figure du théorème de Napoléon Le théorème de Napoléon est un théorème de géométrie portant sur le triangle équilatéral. Bien qu il soit traditionnellement attribué à Napoléon Bonaparte (d où le nom du théorème) qui l’aurait énoncé pour la… …   Wikipédia en Français

  • Général Bonaparte — Napoléon Ier « Napoléon » redirige ici. Pour les autres significations, voir Napoléon (homonymie) et Bonaparte …   Wikipédia en Français

  • Napoleon Bonaparte — Napoléon Ier « Napoléon » redirige ici. Pour les autres significations, voir Napoléon (homonymie) et Bonaparte …   Wikipédia en Français

  • Napoléon Bonaparte — Napoléon Ier « Napoléon » redirige ici. Pour les autres significations, voir Napoléon (homonymie) et Bonaparte …   Wikipédia en Français

  • Napoléon Charles Bonaparte — Napoléon Ier « Napoléon » redirige ici. Pour les autres significations, voir Napoléon (homonymie) et Bonaparte …   Wikipédia en Français

  • Napoléon Ier Bonaparte — Napoléon Ier « Napoléon » redirige ici. Pour les autres significations, voir Napoléon (homonymie) et Bonaparte …   Wikipédia en Français

  • Pierre-Simon de Laplace — Pour les articles homonymes, voir Laplace. Pierre Simon de Laplace Naissance 23 mars …   Wikipédia en Français

  • Empereur Napoléon Ier — Napoléon Ier « Napoléon » redirige ici. Pour les autres significations, voir Napoléon (homonymie) et Bonaparte …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”