Théorème de Thébault

Théorème de Thébault

Le nom de théorème de Thébault ne correspond pas à un théorème précis, mais plutôt à une série de problèmes posés par le mathématicien français Victor Thébault (1882 - 1960).

Sommaire

Le problème de Thébault n°1

Figure du problème de Thébault n°1

Le problème de Thébault n°1 est un problème de géométrie euclidienne portant sur le parallélogramme. Il fut posé par Thébault en 1937[1] qui le démontra en 1938[réf. nécessaire].

Ce théorème peut être considéré comme l'équivalent avec les quadrilatères du théorème de Napoléon qui concerne les triangles.

Problème de Thébault n°1 — Soit un parallélogramme ABCD, quelconque, et extérieurement, quatre carrés construits sur les côtés du parallélogramme. Si M, N, O et P désignent les centres de ces carrés placés comme sur la figure, alors MNOP est également un carré.

La rotation de centre O et d'angle \frac {\pi} {2} transforme C en D, B en D', le carré de côté [CB] a pour image le carré de côté [DA].
Donc N a pour image P, soit ON = OP et l'angle \widehat{NOP} est droit. NOP est un triangle rectangle isocèle en O.

De même par la rotation de centre M et d'angle \frac {\pi} {2}, le carré de côté [DA] a pour image le carré de côté [CB].

Donc P a pour image N ; MP = MN et le triangle NMP est rectangle isocèle en M.

MNOP a ses quatre angles droits et des côtés consécutifs égaux : c'est un carré.

Le problème de Thébault n°2

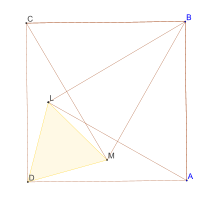
Triangles équilatéraux à l'extérieur du carré
Triangles équilatéraux à l'intérieur du carré


Le problème de Thébault n°2 est un problème de géométrie euclidienne portant sur le triangle équilatéral.

Problème de Thébault n°2 — Soit un carré ABCD. Construisons deux triangles équilatéraux sur deux côtés consécutifs du carré, tous les deux "intérieurs" ou "extérieurs" par exemple ABL et BCM. Alors le triangle LMD est équilatéral.

  • Démonstration par raisonnement géométrique dans le cas externe

Par construction on a DC = DA et CM = AL.

Comme \widehat{DCM} = 90^\circ + 60^\circ = \widehat{LAD} alors les triangles DCM et DAL sont superposables.

Ces deux triangles étant isocèles, on a pour les angles à-la-base \widehat{CDM} = \widehat{LDA} = \frac{180^\circ- (90^\circ+60^\circ)}{2} = 15^\circ.

Ainsi \widehat{MDL} = 90^\circ - \widehat{CDM} - \widehat{LDA} = 90^\circ - 15^\circ - 15^\circ = 60^\circ.

Puisque \widehat{MDL} = 60^\circ et DM = DL, le triangle DML est donc équilatéral.

  • Démonstration par raisonnement géométrique dans le cas interne

Par construction on a AD = AL et CD = CM.

Comme \widehat{DAL} = 90^\circ - 60^\circ = \widehat{MCD} alors les triangles DCM et DAL sont superposables.

Ces deux triangles étant isocèles, on a pour les angles à-la-base \widehat{ADL} = \widehat{MDC} = \frac{180^\circ- (90^\circ-60^\circ)}{2} = 75^\circ.

Ainsi \widehat{MDL} = \widehat{ADL} - \widehat{ADM}

= \widehat{ADL} - (90^\circ-\widehat{MDC})
= 75^\circ - (90^\circ-75^\circ)
= 60^\circ

Puisque \widehat{MDL} = 60^\circ et DM = DL, le triangle DML est donc équilatéral.

Le problème de Thébault n°3

Figure du théorème de Sawayama-Thébault

Le problème de Thébault n°3, aussi connu sous le nom de Théorème de Sawayama-Thébault, est un théorème de géométrie euclidienne portant sur l'alignement de trois points.

La première démonstration connue a été réalisée en 1973 par le mathématicien néerlandais H. Streefkerk[2].
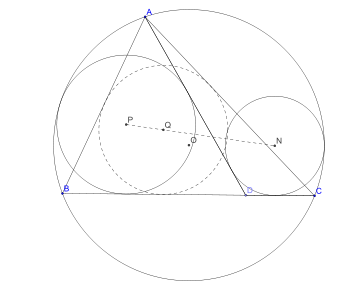
Jean-Louis Ayme[3] a publié, en 2003, une solution purement synthétique de ce problème. Il a également effectué des recherches historiques et a découvert que ce résultat avait été démontré en 1905 par Y. Sawayama[4], instructeur à l'école militaire de Tokyo.

Théorème de Sawayama-Thébault — Soient ABC un triangle quelconque, et D un point de [BC]. Soient Q le centre du cercle inscrit au triangle ABC et \mathcal{C} le cercle circonscrit au triangle ABC. Soient N le centre du cercle tangent à [DC], [DA] et \mathcal{C} et P le centre du cercle tangent à [DB], [DA] et \mathcal{C}.

Alors P, Q et N sont alignés.

Références

  1. ↑ R. Nelsen, Proofs Without Words II, MAA, 2000, p. 19
  2. ↑ H. Streefkerk, Waarom eenvoudig als het ook ingewikkeld kan?, Nieuw Tijdschrift voor Wiskunde, 60 (1972-73) 240–253.
  3. ↑ Ayme, J.-L. "Sawayama and Thebault's Theorem." Forum Geom. 3, 225-229, 2003.
  4. ↑ Y. Sawayama, A new geometrical proposition, Amer. Math. Monthly, 12 (1905) 222–224.

Liens externes


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de Thébault de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Theoreme de Napoleon — Théorème de Napoléon Figure du théorème de Napoléon Le théorème de Napoléon est un théorème de géométrie portant sur le triangle équilatéral. Bien qu il soit traditionnellement attribué à Napoléon Bonaparte (d où le nom du théorème) qui l’aurait… …   Wikipédia en Français

  • Théorème Bonaparte — Théorème de Napoléon Figure du théorème de Napoléon Le théorème de Napoléon est un théorème de géométrie portant sur le triangle équilatéral. Bien qu il soit traditionnellement attribué à Napoléon Bonaparte (d où le nom du théorème) qui l’aurait… …   Wikipédia en Français

  • Théorème de napoléon — Figure du théorème de Napoléon Le théorème de Napoléon est un théorème de géométrie portant sur le triangle équilatéral. Bien qu il soit traditionnellement attribué à Napoléon Bonaparte (d où le nom du théorème) qui l’aurait énoncé pour la… …   Wikipédia en Français

  • Théorème de Napoléon — Figure du théorème de Napoléon Le théorème de Napoléon est un théorème de géométrie portant sur le triangle équilatéral. Bien qu il soit traditionnellement attribué à Napoléon Bonaparte (d où le nom du théorème) qui l’aurait énoncé pour la… …   Wikipédia en Français

  • Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Liste des theoremes — Liste des théorèmes Liste des théorèmes par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le… …   Wikipédia en Français

  • Liste des théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Liste de théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”