- Théorie de la diffraction sur un cristal
-
La théorie de la diffraction sur un cristal modélise l'interaction rayonnement-matière dans le cas où la matière est organisée de manière ordonnée (voir aussi Cristallographie).
Ces phénomènes interviennent essentiellement dans les méthodes d'analyse et d'observation de la matière :
- diffraction des électrons en microscopie électronique en transmission ;
- diffractométrie de rayons X ;
- diffraction de neutrons.
On peut en avoir une approche simplifiée purement géométrique avec l'analogie avec un réseau de diffraction et la loi de Bragg.
Dans une large mesure, l'analyse est indépendante de la nature de la radiation incidente : rayonnement électromagnétique (rayons X) ou particule (électrons, neutrons). Toutefois, la nature du rayonnement intervient pour une analyse plus fine.
Sommaire
Diffusion par les atomes
Le phénomène à la base de la diffraction par un cristal est la diffusion du rayonnement par les atomes. On considère exclusivement une diffusion élastique (le rayonnement ne perd pas d'énergie).
Cette diffusion est anisotrope ; toutefois, pour une première approche, on peut considérer par approximation que cette diffusion est isotrope, c'est-à-dire que l'intensité diffusée par chaque atome est indépendante de la direction de l'espace.
Pour simplifier, on considère un rayonnement monochromatique. Le rayonnement de longueur d'onde λ peut être décrit par sa fonction d'onde ψ en tout point
 de l'espace et à chaque instant t :
de l'espace et à chaque instant t :où φ0 est la phase à l'origine spatiale et temporelle,
 est le vecteur d'onde[1]
est le vecteur d'onde[1]et ω est la pulsation
c étant la vitesse de la lumière.
On choisit arbitrairement l'origine telle que φ0 = 0.
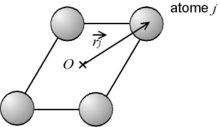
Une maille donnée du cristal est composée de n atomes. Chaque atome j placé en
 diffuse les rayonnements de manière élastique. Considérons l'onde diffusée ayant un vecteur d'onde
diffuse les rayonnements de manière élastique. Considérons l'onde diffusée ayant un vecteur d'onde  :
: puisque l'on considère une diffusion élastique ;
puisque l'on considère une diffusion élastique ;- la direction de
 est la direction de l'espace dans laquelle est diffusée l'onde.
est la direction de l'espace dans laquelle est diffusée l'onde.
La fonction de l'onde diffusée par l'atome j est ψj et s'écrit :
où φ est le déphasage de l'onde en
 par rapport à l'origine spatiale et ƒj est le facteur de diffusion atomique, qui, dans le cas de la diffraction de rayons X, dépend de la densité du nuage électronique de l'atome, donc de sa nature chimique.
par rapport à l'origine spatiale et ƒj est le facteur de diffusion atomique, qui, dans le cas de la diffraction de rayons X, dépend de la densité du nuage électronique de l'atome, donc de sa nature chimique.Le déphasage φ est la somme de deux contributions :
- au point
 considéré, le déphasage φ1 de l'onde incidente par rapport à la source placée à l'origine vaut
considéré, le déphasage φ1 de l'onde incidente par rapport à la source placée à l'origine vaut
-
 ;
;
- le déphasage φ2 de l'onde diffractée entre sa source (l'atome en
 ) et le point
) et le point  vaut
vaut
-
 ;
;
- le déphasage total vaut
-
 .
.
Si l'on définit le vecteur de diffraction
 comme étant
comme étanton a alors :
- Note
- On ne considère qu'une direction de diffusion à la fois, la « direction d'observation » (par exemple direction dans laquelle se trouve le détecteur ponctuel de rayonnement servant à la mesure ou emplacement donné du film photographique ou du détecteur à résolution spatiale), et donc qu'un seul vecteur de diffraction ; mais l'onde est bel et bien diffusée dans toutes les directions simultanément.
Influence de l'organisation de la matière
Facteur de structure
On peut maintenant se placer non plus à l'échelle d'un atome, mais à l'échelle d'une maille cristalline. L'onde ψ' diffractée par la maille est la somme des ondes diffusées par chacun de ses n atomes :
On définit le facteur de structure F comme étant :
on a donc
On a considéré ici que l'onde était diffusée par un atome ponctuel. En toute rigueur, dans le cas de la diffracion de rayons X, l'onde est diffusée par le nuage électronique, qui est une fonction continue de l'espace. Il faut donc définir en chaque point
 de la maille un facteur de diffusion local
de la maille un facteur de diffusion local  , le facteur de structure s'écrivant alors :
, le facteur de structure s'écrivant alors :dv étant l'élément de volume considéré autour de la position
 .
.On voit ainsi que le facteur de structure est la transformée de Fourier de la distribution électronique (pour les rayons X) dans la maille élémentaire.
Facteur de forme
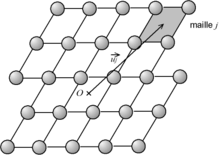
Le cristal est composé de m mailles. La fonction ψ'l de l'onde diffractée par une maille l placée en
 s'écrit :
s'écrit :(ceci se montre de manière similaire à précédemment en considérant le déphasage entre la source et la maille, puis entre la maille et le point
 ).
).L'onde ψ'' diffractée par l'ensemble du cristal est la somme des ondes diffractées par chaque maille, soit :
On définit le facteur de forme
 par :
par :on a donc
 dépend de la forme du cristal, d'où son nom. C'est ce facteur qui intervient dans l'élargissement des raies lorsque la taille des cristallites est faible (inférieure à 1 μm).Article détaillé : Formule de Scherrer.
dépend de la forme du cristal, d'où son nom. C'est ce facteur qui intervient dans l'élargissement des raies lorsque la taille des cristallites est faible (inférieure à 1 μm).Article détaillé : Formule de Scherrer.Intensité diffractée
L'intensité diffractée I dans un point de l'espace
 est proportionnelle au carré de la norme du vecteur de la fonction d'onde :
est proportionnelle au carré de la norme du vecteur de la fonction d'onde :On a un effet d'atténuation en fonction de l'éloignement qui varie selon l'inverse du carré de la distance : il s'agit simplement de la « répartition » de l'énergie sur une sphère (diminution de la densité angulaire). Si l'on corrige ce phénomène, alors l'intensité ne dépend que de la direction de l'espace, que l'on peut donner par le vecteur de l'onde diffractée
 :
: avec
avec  fixé arbitrairement,
fixé arbitrairement,
soit
D'autres facteurs interviennent, notamment la géométrie de l'appareil de mesure, l'optique, l'absorption du rayonnement diffracté par l'atmosphère entre le cristal et le détecteur, etc. Par exemple, l'intensité peut varier selon l'inclinaison du détecteur par rapport à l'échantillon.
Conditions de diffraction
Condition de Laue
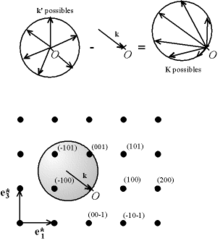
Dans un diagramme de diffraction, un pic (ou un point si c'est une figure 2D) correspond à un maximum d'intensité, c'est-à-dire à un maximum local de F. Intuitivement, F est maximal lorsque les rayons diffusés par les atomes de la cellule sont tous en phase. Si l'on considère deux atomes j et l, on doit avoir
![2\pi \vec{K}\cdot \vec{r}_j \equiv 2\pi \vec{K}\cdot \vec{r}_l [2\pi]](8/528f0f2407ee88295784c8c78b37764e.png) (eq1)
(eq1)
Soit
 la base du réseau direct ; les positions des atomes s'écrivent
la base du réseau direct ; les positions des atomes s'écriventoù xj, yj et zj sont des nombres entiers.
Considérons la base de l'espace réciproque
 avec
avecV étant le volume de la maille
Obtenir la condition générale de diffraction revient à appliquer la condition (eq1) à tous les atomes de la maille deux à deux. On peut montrer que cela impose aux produits scalaires
 d'être entiers (i = 1,2,3). Or les relations de définition de la base réciproque ci-dessus imposent
d'être entiers (i = 1,2,3). Or les relations de définition de la base réciproque ci-dessus imposent
et par conséquent, si l'on écrit le vecteur de diffraction
 comme une combinaison linéaire à coefficients entiers des vecteurs de la base réciproque, alors ses composantes
comme une combinaison linéaire à coefficients entiers des vecteurs de la base réciproque, alors ses composantes  dans la base directe sont bien entières. On définit donc (h,k,l) entiers tels que :
dans la base directe sont bien entières. On définit donc (h,k,l) entiers tels que :L'équation ci-dessus est la condition de diffraction de Laue (dont on peut montrer qu'elle est équivalente à la condition de Bragg.). On interprète les nombres (h k l) comme étant des indices de Miller : si le faisceau incident est de direction constante (
 constant), cela revient à dire que les directions de diffraction
constant), cela revient à dire que les directions de diffraction  donnant un maximum d'intensité sont telles que les
donnant un maximum d'intensité sont telles que les  sont orthogonaux aux plans (h k l), puisqu'on sait que les rangées [h k l]*, définies par leur colinéarité à
sont orthogonaux aux plans (h k l), puisqu'on sait que les rangées [h k l]*, définies par leur colinéarité à  , sont orthogonales aux plans (h k l).
, sont orthogonales aux plans (h k l).On peut ainsi indexer les vecteurs d'onde donnant des maxima d'intensité par les indices de Miller et écrire
 . On peut également indexer les facteurs de structure correspondants :
. On peut également indexer les facteurs de structure correspondants : 
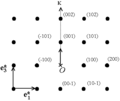
Les lieux des extrémités des
 forment un réseau dans l'espace réciproque, appelé réseau réciproque. On peut donc associer chaque point du réseau réciproque (c'est-à-dire chaque vecteur
forment un réseau dans l'espace réciproque, appelé réseau réciproque. On peut donc associer chaque point du réseau réciproque (c'est-à-dire chaque vecteur  ) à un plan cristallographique, d'indices de Miller (h k l), plan perpendiculaire à
) à un plan cristallographique, d'indices de Miller (h k l), plan perpendiculaire à  .
.Remarque : On définit les indices de Miller h, k, l comme devant être premiers entre eux, les vecteurs
 (où (h', k', l')=i(h,k,l), i étant un entier relatif) se rapportent tous aux mêmes indices h, k, l, ou encore à une direction [h k l]*, à laquelle une infinité de rangées de points de l'espace réciproque sont parallèles. On peut donc maintenant associer à une famille de rangées parallèles d'indices [h k l]* une famille de plans parallèles d'indices (h k l). Ce choix d'indices de Miller premiers entre eux traduit le fait qu'en cristallographie on s'intéresse aux directions (plans et rangées) dans le cristal et non à un plan ou à une rangée particulière dans le cristal.
(où (h', k', l')=i(h,k,l), i étant un entier relatif) se rapportent tous aux mêmes indices h, k, l, ou encore à une direction [h k l]*, à laquelle une infinité de rangées de points de l'espace réciproque sont parallèles. On peut donc maintenant associer à une famille de rangées parallèles d'indices [h k l]* une famille de plans parallèles d'indices (h k l). Ce choix d'indices de Miller premiers entre eux traduit le fait qu'en cristallographie on s'intéresse aux directions (plans et rangées) dans le cristal et non à un plan ou à une rangée particulière dans le cristal.En pratique, lors d'une expérience de diffraction des rayons X, on obtient une figure de diffraction (cliché de Laue par exemple), sur laquelle on visualise les maxima d'intensité. On peut montrer que les symétries d'un réseau direct (associé au cristal) sont les mêmes que celles du réseau réciproque associé (associé aux directions de diffraction) : cela signifie que les symétries de la figure de diffraction doivent se retrouver parmi les symétries du cristal.
Une méthode graphique pour trouver les vecteurs de diffraction : la sphère d'Ewald
Selon la condition de Laue, il y a diffraction si
 (eq2)
(eq2)
donc si
 est un vecteur du réseau réciproque d'un des cristallites éclairés.
est un vecteur du réseau réciproque d'un des cristallites éclairés.Géométrie de Bragg-Brentano
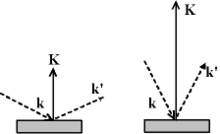
Étudions uniquement le cas où le vecteur de diffraction garde toujours la même orientation par rapport au cristallite (la bissectrice entre le faisceau incident et la direction d'observation est toujours sur la même droite) ; cela signifie que les vecteurs de l'onde incidente et de l'onde diffusée sont toujours symétriques par rapport à cette direction, dans l'espace réel comme dans l'espace réciproque. Cela correspond à la géométrie de Bragg-Brentano, on place le détecteur de manière symétrique à la normale à l'échantillon passant par le centre de celui-ci.
Plaçons-nous dans le cas d'un monocristal. On voit que selon la déviation du faisceau, c'est-à-dire l'angle que fait le faisceau incident avec la direction d'observation, on est en condition de diffraction ou pas.
Supposons maintenant que l'on fasse tourner le cristallite dans tous les sens durant la mesure, ou, ce qui est équivalent, que l'échantillon soit constitué d'une multitude de cristallites orientés dans tous les sens (poudre). Alors, il faut superposer tous les réseaux réciproques pour connaître les déviations donnant un pic/point de diffraction. Cela donne des sphères concentriques ; il y a diffraction si le vecteur de diffraction rencontre une sphère.
Incidence fixe
Considérons qu'à un instant donné, le vecteur de l'onde incidente
 est toujours le même (la position de l'échantillon par rapport à la source ne change pas et la source est ponctuelle). On n'impose pas ici de direction d'observation, le vecteur de l'onde diffusée
est toujours le même (la position de l'échantillon par rapport à la source ne change pas et la source est ponctuelle). On n'impose pas ici de direction d'observation, le vecteur de l'onde diffusée  peut donc prendre toutes les orientations possibles, mais il a toujours la même norme ; il décrit donc une sphère de rayon 1/λ. Les vecteurs de diffraction
peut donc prendre toutes les orientations possibles, mais il a toujours la même norme ; il décrit donc une sphère de rayon 1/λ. Les vecteurs de diffraction  possibles forment donc une sphère de même rayon mais dont le centre est situé en
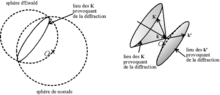
possibles forment donc une sphère de même rayon mais dont le centre est situé en  par rapport à l'origine du réseau réciproque, par définition du vecteur de diffraction. Cette sphère s'appelle la « sphère d'Ewald[2] » (ou « sphère de réflexion »), et elle contient l'origine O du réseau réciproque.
par rapport à l'origine du réseau réciproque, par définition du vecteur de diffraction. Cette sphère s'appelle la « sphère d'Ewald[2] » (ou « sphère de réflexion »), et elle contient l'origine O du réseau réciproque.Les directions dans lesquelles on aura de la diffraction sont donc données par l'intersection de la sphère d'Ewald avec les sphères des
 . L'intersection de deux sphères non concentriques, lorsqu'elle existe, est un cercle. On en déduit que les extrémités des vecteurs de diffraction pour lesquels il y a diffraction forment un cercle, donc que les extrémités des vecteurs d'onde diffusée pour lesquels il y a diffraction décrivent un cercle, c'est-à-dire que : les rayons diffractés forment des cônes.
. L'intersection de deux sphères non concentriques, lorsqu'elle existe, est un cercle. On en déduit que les extrémités des vecteurs de diffraction pour lesquels il y a diffraction forment un cercle, donc que les extrémités des vecteurs d'onde diffusée pour lesquels il y a diffraction décrivent un cercle, c'est-à-dire que : les rayons diffractés forment des cônes. Sphère de résolution, obtenue par la rotation de la sphère d'Ewald autour de l'origine ; son rayon vaut 2/λ
Sphère de résolution, obtenue par la rotation de la sphère d'Ewald autour de l'origine ; son rayon vaut 2/λ
Considérons maintenant que l'on garde le réseau réciproque immobile (monocristal), mais que l'on fait tourner la sphère d'Ewald. On voit que la sphère d'Ewald va balayer une boule de centre O et dont le rayon est le diamètre de la sphère d'Ewald. Les points contenus dans cette « supersphère » correspondent aux différentes conditions de diffraction possibles ; les points à l'extérieur ne peuvent pas, dans les conditions de mesure données (c'est-à-dire pour la longueur d'onde λ donnée), donner de diffraction. Cette « supersphère » est appelée « sphère de résolution », elle a un rayon de 2/λ.
Si λ est trop grand, la sphère de résolution ne contient que le centre du réseau réciproque, la diffraction n'est donc pas possible. C'est la raison pour laquelle il faut recourir à des rayonnements de longueur d'onde suffisamment petite (rayons X ou particules ayant une vitesse suffisamment élevée) pour pouvoir caractériser un réseau cristallin.
 Rotation de la sphère d'Ewald et géométrie de Bragg-Brentano (direction du vecteur de diffraction imposée)
Rotation de la sphère d'Ewald et géométrie de Bragg-Brentano (direction du vecteur de diffraction imposée)
Si l'on se remet dans une géométrie de Bragg-Brentano (direction du vecteur de diffraction fixée), le vecteur de diffraction est obtenu en prenant l'intersection de la sphère avec l'axe de la direction imposée.
Facteur de forme et réseau réciproque
Pour les conditions de diffraction, nous n'avons considéré jusqu'ici que le facteur de structure. Les conditions de diffraction pour un monocristal se représentent comme un réseau ponctuel dans l'espace réciproque.
Ceci ne serait vrai que pour un monocristal de taille « infinie ». Pour un cristallite de taille finie, on a une diffraction au sens diffraction de Fraunhofer ; sur un film photographique, la trace de diffraction n'est donc pas un ensemble de points infiniment petits, mais des taches d'Airy.
Article détaillé : Théorie de la diffraction.Dans l'espace réciproque, la condition de diffraction n'est pas un réseau de points, mais un réseau de taches tridimensionnelles.
La forme de ces taches dans l'espace réciproque est décrite par le facteur de forme. De manière classique en matière de diffraction, la tache du réseau réciproque est plus étendue dans la direction perpendiculaire à la dimension la plus étroite du cristallite.
Si le cristallite est sphérique mais de petite taille (inférieure au micromètre), la tache dans l'espace réciproque sera de symétrie sphérique, la densité décroissant avec le rayon (l'intensité diffractée étant proportionnelle à cette densité).
Si le cristallite est un disque (cylindre aplati dans son axe), la tache de diffraction sera une aiguille (cylindre de faible rayon mais étiré selon son axe).
Théorie cinétique et théorie dynamique
Nous avons exposé ci-dessus la théorie dite « cinétique » de la diffraction. Dans la théorie cinétique, on considère que l'onde diffusée par les nœuds ne diffracte pas elle-même. Cette hypothèse est valable lorsque l'intensité diffractée est faible devant l'intensité incidente, ce qui est le cas avec les rayons X et les neutrons.
Cette hypothèse n'est en général plus valable avec les électrons, sauf dans le cas de la diffraction par une lame mince (dans un microscope électronique en transmission). On a alors recours à la théorie dite « dynamique ».
Notes
- Certains auteurs définissent
 et écrivent
et écrivent 
- Paul Peter Ewald, physicien allemand, 1921
Voir aussi
Liens internes
Liens externes
- (fr) Description pratique de la sphère d'Ewald
- (fr) Diffraction des rayons X - Techniques et études des structures cristallines par le site CultureSciences-Physique de l'ENS Lyon
- Portail de la chimie
- Portail de la physique
- Portail des minéraux et roches
Wikimedia Foundation. 2010.