Conjecture d'Hadwiger
- Conjecture d'Hadwiger
-
Conjecture d'Hadwiger
En théorie des graphes, la conjecture d'Hadwiger est une conjecture très générale sur les problèmes de coloration de graphes. Formulée en 1943 par Hugo Hadwiger, elle énonce que si le graphe complet à k sommets, noté Kk, n'est pas un mineur d'un graphe G, alors il est possible de colorer les sommets de G avec k − 1 couleurs.
Hadwiger a prouvé les cas 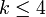 dans le même article qui formule la conjecture. Wagner a prouvé en 1937 que le cas k = 5 est équivalent au théorème des quatre couleurs, et la démonstration en 1976 par Happel et Aken du théorème des quatre couleurs a donc prouvé en même temps la conjecture d'Hadwiger pour le cas k = 5.
dans le même article qui formule la conjecture. Wagner a prouvé en 1937 que le cas k = 5 est équivalent au théorème des quatre couleurs, et la démonstration en 1976 par Happel et Aken du théorème des quatre couleurs a donc prouvé en même temps la conjecture d'Hadwiger pour le cas k = 5.
En 1993, Robertson, Seymour, et Thomas ont prouvé que le cas k = 6 pouvait également se ramener au théorème des quatre couleurs. Ce nouveau résultat les a conduit à vérifier la preuve du théorème des quatre couleurs, et finalement à la simplifier.
La conjecture d'Hadwiger reste ouverte pour k > 6.
Référence
 Portail des mathématiques
Portail des mathématiques
Catégories : Théorème de la théorie des graphes | Conjecture
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Conjecture d'Hadwiger de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Conjecture de Hadwiger — En théorie des graphes, la conjecture de Hadwiger est une conjecture très générale sur les problèmes de coloration de graphes. Formulée en 1943 par Hugo Hadwiger, elle énonce que si le graphe complet à k sommets, noté Kk, n est pas un mineur d un … Wikipédia en Français
Hadwiger conjecture (graph theory) — In graph theory, the Hadwiger conjecture (or Hadwiger s conjecture) states that, if an undirected graph G requires k or more colors in any vertex coloring, then one can find k disjoint connected subgraphs of G such that each subgraph is connected … Wikipedia
Hadwiger conjecture — There are two main conjectures known as the Hadwiger conjecture or Hadwiger s conjecture :* Hadwiger conjecture (graph theory). * Hadwiger conjecture (combinatorial geometry).See also Hadwiger s theorem … Wikipedia
Hugo Hadwiger — in 1973 Hugo Hadwiger (1908 1981) était un mathématicien suisse. Il est connu pour le théorème d Hadwiger en géométrie intégrale, et un certain nombre de conjectures. En particulier, la conjecture d Hadwiger sur la coloration de graphes, est un… … Wikipédia en Français
Hugo Hadwiger — (1908 ndash; 1981) was a Swiss mathematician. He is known for Hadwiger s theorem in integral geometry, and a number of conjectures. He also worked on a Swiss enhancement of the Enigma cipher machine, known as NEMA.His 1957 book Vorlesungen über… … Wikipedia
Borsuk's conjecture — The Borsuk problem in geometry, for historical reasons incorrectly called a Borsuk conjecture, is a question in discrete geometry.ProblemIn 1932 Karol Borsuk has shownK. Borsuk, Drei Sätze über die n dimensionale euklidische Sphäre , Fundamenta… … Wikipedia
Coloration De Graphe — En mathématiques, la coloration de graphe renvoie à un champ d études appartenant à la théorie des graphes. Il s agit de déterminer combien de couleurs différentes suffisent pour colorer entièrement un graphe de telle façon qu aucun nœud du… … Wikipédia en Français
Coloration de graphe — En théorie des graphes, colorer un graphe signifie attribuer une couleur à chacun de ses sommets de manière à ce que deux sommets reliés par une arête soient de couleur différente. Est souvent recherchée l utilisation d un nombre minimal de… … Wikipédia en Français
Nombre chromatique — Coloration de graphe En mathématiques, la coloration de graphe renvoie à un champ d études appartenant à la théorie des graphes. Il s agit de déterminer combien de couleurs différentes suffisent pour colorer entièrement un graphe de telle façon… … Wikipédia en Français
Theoreme quatre couleurs — Coloration de graphe En mathématiques, la coloration de graphe renvoie à un champ d études appartenant à la théorie des graphes. Il s agit de déterminer combien de couleurs différentes suffisent pour colorer entièrement un graphe de telle façon… … Wikipédia en Français
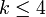 dans le même article qui formule la conjecture. Wagner a prouvé en 1937 que le cas k = 5 est équivalent au théorème des quatre couleurs, et la démonstration en 1976 par Happel et Aken du théorème des quatre couleurs a donc prouvé en même temps la conjecture d'Hadwiger pour le cas k = 5.
dans le même article qui formule la conjecture. Wagner a prouvé en 1937 que le cas k = 5 est équivalent au théorème des quatre couleurs, et la démonstration en 1976 par Happel et Aken du théorème des quatre couleurs a donc prouvé en même temps la conjecture d'Hadwiger pour le cas k = 5.