- Theoreme de Noether (mathematiques)
-
Théorème de Noether (mathématiques)
Pour les articles homonymes, voir Théorème de Noether.Le théorème de Noether, de Emmy Noether (1918), est un théorème de géométrie symplectique.
Sommaire
Principe
Il consiste en: soit M une variété différentielle de dimension n et L un lagrangien indépendant du temps sur M, c'est-à-dire une fonction différentiable
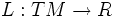. Une symétrie est un difféomorphisme 
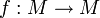tel que l'on ait :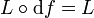
Une symétrie infinitésimale du lagrangien L est un champ de vecteurs V sur U tel que le groupe à un paramètre engendré
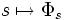soit un groupe de symétries de L. Le théorème de Noether associe à toute symétrie infinitésimale une intégrale première des équations d'Euler-Lagrange de L.Théorème — Si
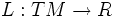est un lagrangien indépendant du temps, et que V est une symétrie infinitésimale de L, alors la fonction G définie sur TM par :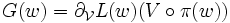
est une intégrale première des équations d'Euler-Lagrange associée à L.
Comme usuellement,
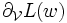désigne la différentielle verticale de L en w, vue comme une forme linéaire sur Tπ(w)M.DémonstrationIntroduisons
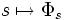, le groupe à un paramètre de difféomorphismes de V. Dérivons par rapport à s en s = 0 l'équation :![L\left[\mathrm d\Phi_s(w)\right]=L(w)](/pictures/frwiki/50/2f56f46ac85f91d0b1d1bc2d3bf8fff6.png)
On trouve la condition que doit satisfaire V pour être une symétrie infinitésimale du lagrangien L :
![\partial_{\mathcal{H}}L(w)(V\circ\pi(w))+ \partial_{\mathcal{V}}L(w)\left[\nabla_wV\right]=0](/pictures/frwiki/100/d97f1ce85c85744879d13b7e20f07dec.png)
où a été introduite une métrique riemannienne arbitraire sur M. Le symbole
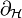désigne la différentielle horizontale. La dépendance de l'équation ci-dessus en la métrique est superficielle. Soit 
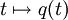une solution des équations d'Euler-Lagrange. Alors, il vient :![\begin{align}
\frac{\mathrm d}{\mathrm dt}G(\dot{q}(t))&=
\left[\nabla_t \partial_{\mathcal{V}}L(\dot{q}(t))\right]\left(W(q(t))\right)+\partial_{\mathcal{V}}L(\dot{q}(t))\left[\nabla_tW\circ q\right]
\\ & = \partial_{\mathcal{H}}L(\dot{q}(t))\left[W(q(t))\right]+\partial_{\mathcal{H}}L(\dot{q}(t))\left[\nabla_tW\circ q\right]
\\ & =0
\end{align}](/pictures/frwiki/54/685a74cf6f4ac797487d3c884c244ce3.png)
D'où le résultat.
Applications
Mouvement à force centrale
Un mouvement à force centrale est le mouvement d'un point matériel de masse m dans un champ de forces dérivant d'un potentiel V = V(r) ne dépendant que du rayon r. C'est le problème variationnel associé au lagrangien L sur
:
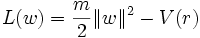
Ce lagrangien est invariant par toutes les rotations dont l'axe passe par l'origine. Un groupe à un paramètre de rotations d'axe D est engendré par un champ de vecteurs de la forme :
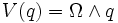
où
désigne le produit vectoriel usuel. Par le théorème de Noether, la fonction :![G_{\Omega}(q,w)=m\dot{q}\cdot \left[\Omega\wedge q\right]=-\Omega\cdot m\left(q\wedge \dot{q}\right)](/pictures/frwiki/50/2af87c226473a00ff1f664e84bebbc89.png)
est une intégrale première du mouvement. En faisant varier le vecteur rotation Ω, on conclut que le vecteur suivant, appelé moment cinétique, est constant :
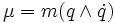
Source
- Pierre Pansu ; Cours de Géométrie différentielle, niveau Master 2 ; [1]
Portail des mathématiques
Catégories : Géométrie symplectique | Théorème d'analyse
Wikimedia Foundation. 2010.
