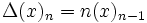Theoreme de Mahler

Theoreme de Mahler

Théorème de Mahler

Le théorème de Mahler offre un analogue du développement en série de Taylor pour les fonctions continues à valeurs p-adiques et dont la variable prend des valeurs p-adiques. Le théorème tire son nom de Kurt Mahler (1903 - 1988).

En combinatoire, le symbole de Pochhammer représente la factorielle indexée :

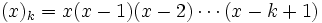(x)_k=x(x-1)(x-2)\cdots(x-k+1)\,.

On note Δ l'opérateur de différence défini par

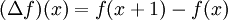(\Delta f)(x)=f(x+1)-f(x)\,.

Alors nous avons

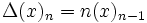
\Delta(x)_n=n(x)_{n-1}\,

c’est-à-dire que le lien de parenté entre l'opérateur Δ et cette suite de polynômes est analogue au lien entre la différentiation réelle et la suite dont le n-ième terme est xn.

Énoncé — Si f est une fonction continue à valeurs p-adiques et dont la variable prend des valeurs p-adiques, alors

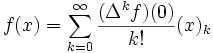f(x)=\sum_{k=0}^\infty\frac{(\Delta^k f)(0)}{k!}(x)_k\,.

Contrairement au cas des séries à valeurs complexes où les conditions sont très contraignantes (cf. théorème de Carson), on a seulement besoin de la continuité.

Si f est un polynôme à coefficients dans n'importe quel corps de caractéristique nulle, l'identité reste valable.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de Mahler ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de Mahler de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Théorème de mahler — Le théorème de Mahler offre un analogue du développement en série de Taylor pour les fonctions continues à valeurs p adiques et dont la variable prend des valeurs p adiques. Le théorème tire son nom de Kurt Mahler (1903 1988). En combinatoire, le …   Wikipédia en Français

  • Théorème de Mahler — Le théorème de Mahler offre un analogue du développement en série de Taylor pour les fonctions continues à valeurs p adiques et dont la variable prend des valeurs p adiques. Le théorème a été démontré par Kurt Mahler[1]. En combinatoire, le… …   Wikipédia en Français

  • Mahler measure — In mathematics, the Mahler measure M(p) of a polynomial p is Here p is assumed complex valued and is the Lτ norm of p (although this is not a true norm for values of τ < 1). It can be shown that if …   Wikipedia

  • Kurt Mahler — Pour les articles homonymes, voir Mahler (homonymie). Kurt Mahler en 1970 Kurt Mahler, né le 26 juillet 1903, à Krefeld, en …   Wikipédia en Français

  • Medida de Mahler — En matemáticas, la medida de Mahler M(p) de un polinomio p es Aquí se presupone que p toma valores complejos y es la número algebraico α se define como la medida de Mahler del polinomio mínimo de α sobre Q. La medida se …   Wikipedia Español

  • Liste de théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Liste Des Matières De La Théorie Des Nombres — Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 …   Wikipédia en Français

  • Liste des matieres de la theorie des nombres — Liste des matières de la théorie des nombres Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 …   Wikipédia en Français

  • Liste des matières de la théorie des nombres — Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 Test de primalité e …   Wikipédia en Français

  • Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

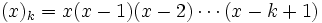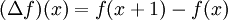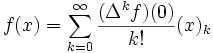Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”