- Theoreme d'Ehrenfest
-
Théorème d'Ehrenfest
Le théorème d'Ehrenfest, du nom du physicien Paul Ehrenfest, relie la dérivée temporelle de la valeur moyenne d'un opérateur quantique au commutateur de cet opérateur avec le hamiltonien
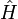 du système.
du système.Sommaire
Théorème
Le théorème d'Ehrenfest affirme que la valeur moyenne d’un opérateur
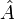 est donnée par :
est donnée par :Ce théorème s'adapte parfaitement à la représentation de Heisenberg en mécanique quantique, et il est étroitement lié au théorème de Liouville de la mécanique hamiltonienne, qui utilise le crochet de Poisson au lieu d'un commutateur. En fait, c'est une loi empirique générale qu'un théorème de mécanique quantique qui contient un commutateur puisse devenir un théorème de mécanique classique en changeant le commutateur par un crochet de Poisson et en multipliant par
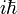 .
.où
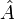 est un opérateur quantique quelconque et
est un opérateur quantique quelconque et 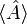 sa valeur moyenne.Démonstration du théorème
sa valeur moyenne.Démonstration du théorèmeSoit A une grandeur physique représentée par l'opérateur autoadjoint
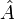
En dérivant
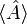 , on obtient
, on obtientOn remarque que
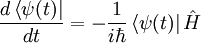 et
et 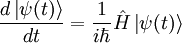
On insère ces deux expressions dans l'expression précédente et on obtient
Avec
![\hat{A}\hat{H} - \hat{H}\hat{A} = [\hat{A},\hat{H}]](/pictures/frwiki/50/23eadb55ce5ac64842f8f19c82de6146.png) , on obtient finalement
, on obtient finalementRelations d'Ehrenfest
Pour l'exemple très général d'une particule massive se déplaçant dans un potentiel, l'hamiltonien est simplement
où x est la position de la particule. On a alors les relations suivantes :
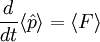
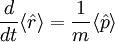
En combinant ces deux relations, on retrouve une équation similaire à celle de Newton en mécanique classique :
Opérateur impulsion
On suppose qu'on veut connaître la varitation instantanée de la quantité de mouvement p. En utilisant le théorème d'Ehrenfest, on a
puisque p commute avec lui-même et puisque lorsqu'il est représentée avec les coordonnées d'espace, l'opérateur d'impulsion
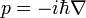 soit
soit 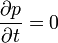 .
.
Donc
Ensuite en appliquant la règle du produit, on a
on voit apparaître la seconde loi de Newton. C'est un exemple du principe de correspondance ; le résultat signifie, comme la deuxième loi de Newton, que le mouvement net d'un grand nombre de particules est exactement donné par la valeur moyenne d'une particule seule.
Opérateur position
On peut aussi obtenir une autre relation en remplacant l'opérateur
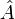 par
par 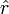 :
:En utilisant les relations de communtations,
on obtient :
Voir aussi
Bibliogrphie
- C. Cohen-Tannoudji, B. Diu et F. Laloë, Mécanique quantique [détail des éditions]
- Portail de la physique
Catégories : Mécanique quantique | Théorème de physique
Wikimedia Foundation. 2010.

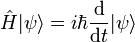
![\frac{d\langle \hat{A}\rangle}{dt} = \frac{1}{i\hbar} \left \langle \psi (t) \right |[\hat{A},\hat{H}]\left | \psi (t) \right \rangle + \langle \frac{\partial \hat{A}}{\partial t}\rangle](/pictures/frwiki/98/b55daf155ca8177aa5c19358c8a6372d.png)
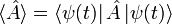
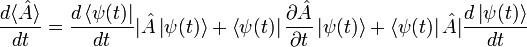
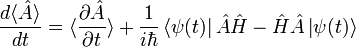
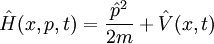
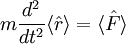
![\frac{d}{dt}\langle p\rangle = \frac{1}{i\hbar}\langle [p,H]\rangle + \langle \frac{\partial p}{\partial t}\rangle = \frac{1}{i\hbar}\langle [p,V(x,t)]\rangle](/pictures/frwiki/98/b04a10da601d90b32f77dfd393b5a068.png)
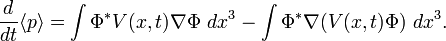
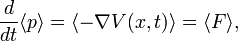
![\frac{d}{dt}\langle \hat r\rangle = \frac{1}{i\hbar}\langle [\hat r,\hat H]\rangle + \langle \frac{\partial \hat r}{\partial \hat t}\rangle = \frac{1}{i\hbar}\langle [\hat r,\frac{\hat p^2}{2m}]\rangle](/pictures/frwiki/100/da14b8fdaf33e6e0312f35932f6653b0.png)
![[\hat r, \frac{\hat p ^2}{2m}] = \frac{i \hbar }{m} \hat p](/pictures/frwiki/56/8b2a7ef515f4cf6233ddafc860b39e73.png)