Theoreme d'Erdos
Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme d'Erdos de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Theoreme d'Erdős — Théorème d Erdős Tout entier n s écrit sous la forme : où . par exemple : 1 = 12 2 = − 12 − 22 − 32 + 42 3 = − 12 + 22 − 32 − 42 + 52 4 = − 12 − 22 + 32 … Wikipédia en Français
Théorème d'Erdős — Tout entier n s écrit sous la forme : où . par exemple : 1 = 12 2 = − 12 − 22 − 32 + 42 3 = − 12 + 22 − 32 − 42 + 52 4 = − 12 − 22 + 32 … Wikipédia en Français
Theoreme d'Erdos- Kac — Théorème d Erdős Kac Le théorème d Erdös Kac est le premier exemple d étude de la convergence faible de fréquences des fonctions additives [FAUX: Le theoreme de Schoenberg (annees 20) donne la loi limite de log(phi(n)/n)) ou phi est l indicatrice … Wikipédia en Français
Theoreme d'Erdős- Kac — Théorème d Erdős Kac Le théorème d Erdös Kac est le premier exemple d étude de la convergence faible de fréquences des fonctions additives [FAUX: Le theoreme de Schoenberg (annees 20) donne la loi limite de log(phi(n)/n)) ou phi est l indicatrice … Wikipédia en Français
Théorème d'Erdős- Kac — Le théorème d Erdös Kac est le premier exemple d étude de la convergence faible de fréquences des fonctions additives [FAUX: Le theoreme de Schoenberg (annees 20) donne la loi limite de log(phi(n)/n)) ou phi est l indicatrice d Euler], et est… … Wikipédia en Français
Théorème d'erdős- kac — Le théorème d Erdös Kac est le premier exemple d étude de la convergence faible de fréquences des fonctions additives [FAUX: Le theoreme de Schoenberg (annees 20) donne la loi limite de log(phi(n)/n)) ou phi est l indicatrice d Euler], et est… … Wikipédia en Français
Théorème d'Erdős-Mordell — Figure du Théorème d Erdős Mordell : MA + MB + MC ≥ 2(MH + MK +ML) Le théorème d Erdős Mordell est un théorème de géométrie euclidienne portant sur le triangle. Son nom provient des mathématiciens Paul Erdős qui l a conjecturé en 1935 et… … Wikipédia en Français
Théorème d'Erdős-Kaplansky — En mathématiques, plus précisément en algèbre linéaire, on sait qu un espace vectoriel E de dimension finie est isomorphe à son dual. En revanche, si E est de dimension infinie, il n est jamais isomorphe à son dual. Cela résulte du théorème d… … Wikipédia en Français
Théorème d'Erdős-Kac — Le théorème d Erdős Kac en théorie des nombres est un exemple d étude de la convergence faible de fréquences des fonctions additives, et est considéré comme fondamental en théorie probabiliste des nombres (en). Il est relatif à la fonction… … Wikipédia en Français
Théorème d'Erdős-Suranyi — Tout entier n s écrit sous la forme : où . Les décompositions des premiers entiers sont : 0 = 02 1 = 12 2 = − 12 − 22 − 32 + 42 3 = − 12 + 22 − 32 − 42 + 52 Démonstration On démontre aisément … Wikipédia en Français

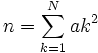
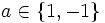 .
.