Système arithmétique positionnel

Numérations selon les cultures
Numération arabo-indienne
arabe khmer indienne	mongole thaï
Numérations à l’origine chinoise
chinoise japonaise	à bâtons suzhou
Numérations alphabétiques
arménienne cyrillique d'Âryabhata éthiopienne	hébraïque grecque tchouvache
Autres systèmes
attique brahmi champs d'urnes colombienne égyptienne étrusque	forestière inuite maya mésopotamienne romaine
Notations positionnelles par base
Décimal (10)
2, 4, 8, 16, 32, 64
1, 3, 6, 9, 12, 20, 24, 30, 36, 60, plus…

La notation positionnelle est un procédé d'écriture des nombres, dans lequel chaque position est reliée à la position voisine par un multiplicateur, appelé base du système de numération. Chaque position peut être représentée par un symbole ou par une quantité limitée de symbole. La valeur d'une position est celle du symbole de position ou celle de la précédente position apparente multipliée par la base. Le nombre de symboles nécessaires est au moins égal à la base ou à la plus grande base auxiliaire utilisée. Le système décimal usuel utilise dix symboles, plus les symboles pour les nombres signés et les nombres à virgule, tandis que le système sexagésimal babylonien se sert d'un système décimal auxiliaire pour chaque position.

Sommaire 1 Systèmes de notation 1.1 Notations hybrides 1.2 Notations positionnelles et additives 1.3 Notations exclusivement positionnelles 2 Symboles positionnels 3 Historique 3.1 Période antique 3.2 Moyen Âge 4 Anecdotes 5 Voir aussi

Systèmes de notation

Plusieurs notations positionnelles, dont certaines hybrides (positionnelles et additives) permettent de représenter les nombres. Voici différentes manières d'écrire le nombre 9018 dans quelques uns de ces systèmes.

Notations hybrides

Les notations hybrides utilisent des symboles représentant les puissance de la base, comme dans les numérations chinoise et japonaise. Ainsi, 十 = 10, 百 = 10², 千 = 10³, 万 = 10⁴ dans le système japonais. Ces numérations utilisent, comme pour les puissances de la base, des symboles représentant les sous-puissance de la base. Ainsi, 割 = 10^-1, 分 = 10^-2, 厘 = 10^-3, 毛 = 10^-4 dans le système japonais.

• Exemple

9018 s'écrit 九千十八 avec le système utilisé pour la numération japonaise (décimale), soit 9 × 1000 + [1×]10 + 8.

Notations positionnelles et additives

Pour la numération babylonienne, à caractère sexagésimale, les nombres étaient formés de manière additive jusqu'à 60, les valeurs ainsi obtenues étant combinés selon le principe positionnel.

• Exemple

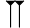
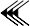
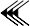
9018 s'écrit avec le système utilisé pour la numération babylonienne (sexagésimale), soit 2[×3600] + 30[×60] + 30 + 8, ou 2,30,38 avec la virgule comme séparateur de positions.

Notations exclusivement positionnelles

• Avec des chiffres formés par une juxtaposition d'éléments

9018 s'écrit :

avec le système utilisé pour la numération maya (vigésimale, mais irrégulière), soit 1[×7200] + 5[×360] + 0[×20] + 18, ou 1,05,00,18 avec la virgule comme séparateur de positions.

• Avec base auxiliaire

9018 s'écrit 2,30,38 avec le système (sexagésimal) utilisé pour la traduction des textes mésopotamiens, soit 2[×3600] + 30[×60] + 38.

• Sans base auxiliaire, sans zéro

9018 s'écrit 8X18 dans le système positionnel expérimental sans zéro (décimal), soit 8[×1000] + 10[×100] + 1[×10] + 8, ou 8,10,1,8, avec la virgule comme séparateur de positions.

• Sans base auxiliaire, avec zéro

9018 s'écrit ๙๐๑๘ avec le système utilisé pour la numération thaï (décimale), soit 9[×1000] + 0[×100] + 1[×10] + 8, ou 9018, de même qu'avec nos chiffres arabo-indiens.

Symboles positionnels

De même que dans notre système, aucun symbole n'est employé pour séparer chaque position dans les systèmes de numération babylonien, maya et thaï. Cependant, en l'absence de zéro positionnel, dans le système babylonien, 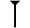pouvait signifier, par exemple, aussi bien un que soixante. Cependant, dans d'autres écritures, ces marqueurs de position s'avèrent systématiques, comme la virgule utilisée pour la traduction des textes mésopotamiens.

Seuls les nombres entiers avaient une représentation dans le système de numération maya. Dans la numération babylonienne, contrairement à ponctuation que nous plaçons entre le chiffre des unités et celui des dixièmes, aucun marqueur de position ne séparait la partie entière de la partie fractionnaire du nombre. Ainsi, 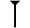pouvait, par exemple, non seulement signifier un et soixante, mais aussi un soixantième dans le système babylonien. Quant à elle, la numération thaï utilise, comme dans notre système, un marqueur de position pour séparer les puissances de mille.

Historique

Période antique

La mise en place des systèmes arithmétiques positionnels, en particulier du système décimal, fut initiée par les chinois dans leur numération chinoise au II^e siècle avant J-C, puis finalisée vers l'an 500 de l'ère chrétienne en Inde.

Dans l'Antiquité, on utilisait exclusivement de nombreux systèmes non-positionnels, dont l'exemple le plus connu est la numération romaine, où le nombre trente-huit, par exemple, s'écrit à l'aide de pas moins de sept chiffres (XXXVIII), tandis que le nombre cinquante, se contente d'un seul (L). Il est clair que, dans un tel système de notation, une simple opération comme une multiplication se révèle pratiquement impossible à effectuer sans abaque (boulier, tablettes de calcul à jetons, ou autre outil de calcul).

Moyen Âge

C'est par l'intermédiaire d'Al-Khuwarizmi (qui a donné le mot algorithme) que les Européens ont pris connaissance de l'existence de la numération indienne positionnelle. Vers l'An mille, après avoir mis plus de cinq siècles à s'intéresser à l'existence de ce nouveau système, ils le rejetèrent encore pendant près de cinq siècles. Et pourtant des ecclésiastiques ouverts comme le français Gerbert d'Aurillac, le futur pape de Rome Sylvestre II, qui le premier décrit le système qu'utilisaient les Arabes d'Espagne, ne dit rien dans ce sens. Il décrit le nouveau système avec intérêt et bienveillance.

C'est pourquoi l'Europe du Moyen Âge continuait à faire sa petite comptabilité moyennant des bouliers et des jetons, écrivant les résultats dans des textes en latin et, naturellement, en utilisant les chiffres romains non-positionnels. On peut dire que le système arithmétique positionnel, tout comme les chiffres dits arabes, n'était pas utilisé dans l'Europe du Moyen Âge, sauf par des utilisateurs isolés et suspects aux yeux des autres, comme par exemple le mathématicien italien Fibonacci et plus tard, bien sûr, le mathématicien français Nicolas Chuquet.

C'est seulement à la Renaissance, avec le réveil des sciences, que l'Europe enfin comprit, que l’on ne pouvait pas faire l'impasse de ce nouveau système. Mille ans (!) après son invention en Inde. Enfin tout le monde occidental admet, qu'en fait, cela est beaucoup plus simple comme ça. La lutte entre les abacistes et les algoristes, qui avait duré près de trois siècles, conduit enfin à la victoire du camp de ces derniers.

La notation positionnelle a rendu possible une représentation simple de tous les nombres. Ce fut une des découvertes majeures de l'histoire des mathématiques. Elle a permis le développement de l'arithmétique, et des mathématiques modernes.

Anecdotes

• Le système de numération Shadok est quaternaire et formé des nombres ga (0), bu (1), zo (2), meu (3).

C'est un système de numération par position : quand on a quatre Shadoks, on n'a plus de nouveau mot pour les compter, alors on les met dans une grande poubelle, et on dit bu pour dire que l'on a une grande poubelle et ga pour dire qu'il n'y a pas de shadoks à côté, d'où buga. De même, lorsque l'on a quatre grandes poubelles, on prend une poubelle à poubelle, et on dit bugaga, et ainsi de suite. C'est le principe même de la numération de position.

• Le système mésopotamien à base 60 a survécu dans notre façon de subdiviser les heures et les degrés, tous deux en minutes et secondes. Dans certaines circonstances, les deux points sont utilisés comme un séparateur de positions sexagésimales. Ainsi, 13 h 20 min 15 s s'écrit aussi 13:20:15.

Voir aussi

• Numération
• Système de numération
• Écriture décimale positionnelle
• Base (arithmétique)
• Chiffre

Base de numération positionnelle
1 à 9	unaire (1), binaire (2), trinaire (3), quaternaire (4), quinaire (5), sénaire (6), septénaire (7), octal (8), nonaire (9)
10 à 60	décimal (10), duodécimal (12), hexadécimal (16), vicésimal (20), sexagésimal (60),
Autre base	base d'or (φ),
Notions	base • chiffre • nombre • notation positionnelle • numération

• Portail des mathématiques