- Numeration a batons
-
Numération à bâtons
Numérations selon les cultures Numération arabo-indienne arabe
khmer
indiennemongole
thaïNumérations à l’origine chinoise chinoise
japonaiseà bâtons
suzhouNumérations alphabétiques arménienne
cyrillique
d'Âryabhata
éthiopiennehébraïque
grecque
tchouvacheAutres systèmes attique
brahmi
champs d'urnes
colombienne
égyptienne
étrusqueforestière
inuite
maya
mésopotamienne
romaineNotations positionnelles par base Décimal (10) 2, 4, 8, 16, 32, 64 1, 3, 6, 9, 12, 20, 24, 30, 36, 60, plus… La numération à bâtons (chinois : 算筹/算籌, pinyin : suànchóu) remonte au 1er siècle avant J.-C. et est originaire de la civilisation chinoise antique. Il s'agit d'une numération de position à base 10 comportant dix-huit symboles, avec un vide pour représenter le zéro.
En raison de son usage très approprié au calcul, beaucoup de mathématiciens chinois de l'époque adoptèrent cette numération pour leurs travaux.
Chiffres
La numération à bâtons possède deux séries de chiffres allant de 1 à 9. Dans cet article, nous appellerons l'une des deux séries par la lettre A et l'autre par la lettre B. Dans les deux séries, le 0 est représenté par un espace vide.
Série 0 1 2 3 4 5 6 7 8 9 A 
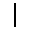
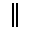
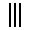
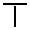
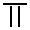
B 
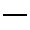
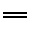
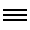
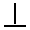
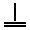
Construction de nombres
En tant que système positionnel à base 10, chaque chiffre représente un coefficient d'une puissance de 10 selon la place qu'il occupe. Le chiffre le plus à droite est l'unité du nombre, celui à sa gauche, la dizaine, etc.
Cependant, le chiffre zéro représenté par un vide pose problème : deux nombres tels 62 et 620 seraient difficilement distinguables.
De plus, lorsque l'on pose les bâtons, si
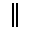représente le chiffre 2 et 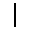représente le chiffre 1, il n'est pas évident de savoir si 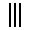représente 3, 12 ou 21 (ou même 30, 120 ou 210).C'est pour pallier ces confusions possibles que la numération possède deux séries de chiffres.
La série A sert à noter les chiffres des puissances paires de 10 (unités, centaines, dizaines de millier, ...) et la série B est utilisée pour les puissances de 10 impaires (dizaines, milliers, ...).
Ainsi, nous pouvons écrire les nombres suivants :
- 4 :
- 72 :
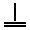
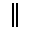
- 256 :
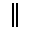
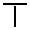
- 308 :
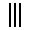
- 1 007 :
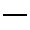
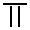
- 81 753 :
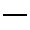
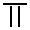
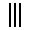
- 1,95 :
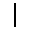
Il n'y a pas de moyen (comme dans la numération babylonienne) de différencier les nombres décimaux des entiers. Seuls leur position sur la table à calcul et le texte qui les accompagne les différencient. Les zéros consécutifs sont symbolisés par un espace d'autant plus grand qu'ils sont nombreux.
Voir aussi
Portail de l’écriture
Portail des mathématiques
Portail du monde chinois
Catégories : Numération | Culture chinoise - 4 :
Wikimedia Foundation. 2010.
