Suites de Cauchy

Suites de Cauchy: Suite de Cauchy

Pour les articles homonymes, voir Cauchy.

Augustin Louis Cauchy

En analyse mathématique, une suite de Cauchy est une suite de réels, de complexes, de points d'un espace métrique, ou d'un espace topologique uniforme dont les termes se rapprochent à partir d'un certain rang. Ces suites sont celles susceptibles de converger. Elles sont au centre de la définition de complétude. Les suites de Cauchy portent le nom du mathématicien français Augustin Louis Cauchy.

Il existe une notion équivalente pour les filtres : les filtres de Cauchy.

Sommaire

1 Suite réelle ou complexe de Cauchy

2 Suite de Cauchy dans un espace métrique

2.1 Définition

2.2 Propriétés

2.3 Approche non standard

3 Suite de Cauchy dans un espace uniforme

3.1 Définitions

4 Voir aussi

5 Notes et références

5.1 Notes

5.2 Références

Suite réelle ou complexe de Cauchy

La différence des termes consécutifs de la suite 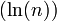$(\ln(n)) \$ tend vers 0. On peut préciser la vitesse de convergence :
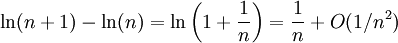$\ln(n+1)-\ln(n)=\ln\left(1+\frac{1}{n}\right)=\frac{1}{n}+O(1/n^2)$ .
Cependant, $ln(2 n) - ln(n) = ln(2)$ ne converge pas vers 0 lorsque n tend vers l'infini. Cette constatation mesure un défaut de non convergence de la suite $ln(n)$ et conduit à énoncer un critère de convergence, le critère de Cauchy.

Une suite de réels ou de complexes est dite de Cauchy lorsque les termes de la suite se rapprochent uniformément les uns des autres en l'infini au sens où :
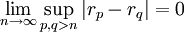$\lim_{n\rightarrow \infty}\sup_{p,q>n}|r_p-r_q|=0$ .
Cette dernière condition se réécrit classiquement à l'aide de quantificateurs universels et existentiels :
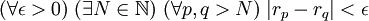$(\forall\epsilon>0)\; (\exists N\in \mathbb N)\; (\forall p,q>N)\; |r_p-r_q|<\epsilon\;$ , ou encore : 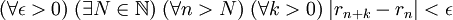$(\forall\epsilon>0)\; (\exists N\in \mathbb N)\; (\forall n>N)\; (\forall k>0)\; |r_{n+k}-r_n|<\epsilon\;$ .
Critère de Cauchy : Une suite 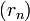$(r_n) \$ de nombres réels (respectivement complexes) converge dans |R (respectivement C) si et seulement si c'est une suite de Cauchy.

Suite de Cauchy dans un espace métrique

Définition

Une suite 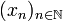$(x_n)_{n\in\mathbb N}$ dans un espace métrique $(E, d)$ est dite suite de Cauchy (ou de Cauchy) si pour tout réel 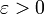$\varepsilon>0$ , il existe un entier naturel $N$ tel que pour tous entiers 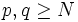$p,q\geq N$ , la distance $d (x p, x q)$ soit inférieure à $\varepsilon$ :
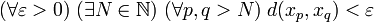$(\forall \varepsilon>0)\; (\exists N\in \mathbb N)\; (\forall p,q>N)\; d(x_p,x_q)<\varepsilon$ .
Les inégalités peuvent être prises indifféremment larges ou strictes. Lorsque certains ouvrages introduisent la notion de suite de Cauchy uniquement pour les suites de réels, c'est exactement la même définition. La distance d est simplement à remplacer par la valeur absolue de la différence.

Intuitivement, les termes de la suite deviennent de plus en plus proches les uns des autres d'une certaine façon qui suggère que la suite doit avoir une limite dans l'espace. Les suites convergentes sont effectivement de Cauchy, mais néanmoins la réciproque n'est pas vraie en toute généralité. Par exemple, il existe des suites de rationnels qui sont de Cauchy dans $\mathbb Q$ mais qui ne convergent pas dans $\mathbb Q$ .

Exemple : l'ensemble A des nombres rationnels r tels que 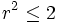$r^2\leq 2$ est borné. Pour tout entier n, il existe un rationnel $r n$ dans A tel que $r n + 1 / n$ n'appartienne pas à A. La suite $(r n)$ est une suite de rationnels positifs et pour p>n, une discussion donne : $| r n - r p | < 1 / n$ . Donc, cette suite est de Cauchy et vérifie : 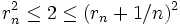$r_n^2\leq 2\leq (r_n+1/n)^2$ . Si elle converge vers un rationnel l, par passage à la limite dans les inégalités, on obtiendrait $l 2 = 2$ . La limite l serait une racine carrée rationnelle de 2, d'où une contradiction. La preuve de l'irrationalité de $\sqrt{2}$ n'utilise pas l'existence des réels. L'exemple ici donné ne suppose pas forcément connu les réels.

C'est la raison pour laquelle un espace métrique dans lequel toute suite de Cauchy converge est dit complet. L'ensemble des nombres réels est complet, et la construction standard de l'ensemble des nombres réels utilise les suites de Cauchy de nombres rationnels (voir la construction des nombres réels à ce sujet).

Article détaillé : espace complet.

Propriétés

Dans un espace métrique, toute suite convergente est de Cauchy.

Supposons qu'une suite $x = (x n)$ d'un espace métrique $(X, d)$ converge vers une limite l. Alors, pour tout $ε > 0$ , il existe un entier $N$ suffisamment grand tel que pour tout n>N on a : $d (x n, l) < ε$ . L'inégalité triangulaire implique que pour p,q>N, on a :
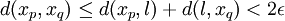$d(x_p,x_q)\leq d(x_p,l)+d(l,x_q)<2\epsilon$ .
La suite x est donc bien de Cauchy.

Toute suite de Cauchy est bornée.

Soit $(x n)$ une suite de Cauchy. Appliquons la définition pour $ε = 1$ . Il existe un entier naturel $N$ vérifiant $d (x p, x q) < 1$ pour 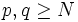$p,q\geq N$ . En particulier, pour p>N, on a : $d (x p, x N) < 1$ . Donc, à partir du rang N, les termes de la suite appartiennent à une boule de rayon 1. Par conséquent, la suite x est bornée.

Une suite de Cauchy a au plus une valeur d'adhérence. Si elle possède une valeur d'adhérence, alors elle converge.

Une suite convergente dans un espace métrique possède une unique valeur d'adhérence, à savoir sa limite. La première affirmation découle de fait de la seconde. Soit x une suite de Cauchy de $(X, d)$ admettant une valeur d'adhérence l. Démontrons que x converge vers l. Choisissons un réel arbitraire $ε > 0$ . Comme x est une suite de Cauchy, il existe un entier naturel N tel que pour tous p, et q>N, on a : $d (x p, x q) < ε$ . Mais l est la limite d'une certaine suite extraite de $(x n)$ , qu'on note 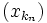$(x_{k_n})$ où $(k n)$ est une suite strictement croissante d'entiers naturels. Il existe un entier P tel que pour tout n>P, on a : 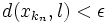$d(x_{k_n},l)<\epsilon$ . On peut choisir P de sorte que k_P soit strictement plus grand que N. Par inégalité triangulaire, pour n>N, il vient :
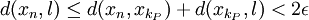$d(x_n,l)\leq d(x_n,x_{k_P})+d(x_{k_P},l)<2\epsilon$ .
Un tel entier N pouvait être défini pour tout réel $ε > 0$ , la suite x converge vers l.

L'image d'une suite de Cauchy par une application uniformément continue est de Cauchy.

Soit f une application uniformément continue d'un espace métrique $(X, d X)$ vers $(Y, d Y)$ , et soit x une suite de Cauchy de $(X, d X)$ . Fixons $ε > 0$ . Comme f est uniformément continue, il existe $η > 0$ tel que, pour tous x et x' de X, on a :
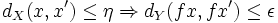$d_X(x,x')\leq \eta\Rightarrow d_Y(fx,fx')\leq \epsilon$ .
Comme x est de Cauchy, il existe un entier naturel N tel que pour tous p, q>N, on a : $d X (x p, x q) < η$ . A fortiori, pour p, q>N, on a par l'implication ci-dessus : $d Y (f x p, f x q) < ε$ . La suite $(f (x n))$ est donc elle-même de Cauchy.

Dans les espaces vectoriels normés, les suites de Cauchy forment un sous-espace de l'espace des suites.

Une homothétie d'un espace vectoriel normé est une application lipschitzienne, donc uniformément continue. L'image d'une suite de Cauchy par une application uniformément continue étant de Cauchy, si x est une suite de Cauchy d'un espace vectoriel normé E et r est un réel, alors r.x est une suite de Cauchy. 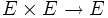De même, la somme de deux suites de Cauchy de E est une suite de Cauchy de E : la somme vectorielle définit une application uniformément continue $E\times E\rightarrow E$ .

Dans une algèbre normée, un produit de suites de Cauchy est de Cauchy.

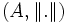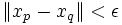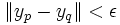Considérons deux suites de Cauchy x et y dans une algèbre normée $(A,\|.\|)$ . Elles sont bornées (propriété précédemment établie) ; notons alors M un majorant des suites $(x n)$ et $(y n)$ . Considérons leur produit $x y$ (produit terme à terme). Par définition des suites de Cauchy, pour $ε > 0$ , il existe un entier N tel que pour tous p, q>N, on a : $\|x_p-x_q\|<\epsilon$ et $\|y_p-y_q\|<\epsilon$ . Par inégalité triangulaire, il vient, pour p,q>N :
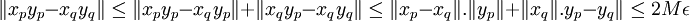$\|x_py_p-x_qy_q\|\leq \|x_py_p-x_qy_p\|+\|x_qy_p-x_qy_q\|\leq \|x_p-x_q\|.\|y_p\|+\|x_q\|.y_p-y_q\|\leq 2M\epsilon$ .
La seconde inégalité provient de la sous-multiplicativité de la norme. La suite $x y$ est donc de Cauchy.

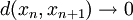Dans un espace ultramétrique (X,d), une suite $(x n)$ est de Cauchy si et seulement si $d(x_n,x_{n+1})\rightarrow 0$ .

Seul le sens réciproque n'est pas toujours vérifié et utilise l'inégalité ultramétrique. Supposons donc 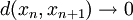$d(x_n,x_{n+1})\rightarrow 0$ . Pour $ε > 0$ , il existe un entier naturel N tel que pour tout n>N, on a : $d (x n, x n + 1) < ε$ . Par récurrence sur k, on montre que pour tout n>N, $d (x n, x n + k) < ε$ . Cette propriété est vérifiée par choix de N pour k=1. Supposons-la établie au rang n, et regardons l'incrémentation. L'inégalité ultratriangulaire donne :
$d(x_n,x_{n+k+1})\leq \max\left[d(x_n,x_{n+1}),d(x_{n+1},x_{n+1+k})\right]\leq \epsilon$ .
La seconde inégalité provient de l'application de l'hypothèse de récurrence.

Approche non standard

En analyse non standard, pour un espace métrique standard $(X, d)$ , il existe une définition équivalente mais pratique de la notion de suite de Cauchy.

Dans un espace métrique standard $(X, d)$ , une suite standard x est de Cauchy si et seulement si pour tous entiers naturels non standards n et p, le réel $d (x p, x q)$ est infiniment petite :

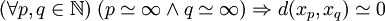$(\forall p,q\in \mathbb N)\; (p\simeq \infty\wedge q\simeq \infty)\Rightarrow d(x_p,x_q)\simeq 0$ .
En effet, si x est une suite de Cauchy, alors pour tout réel $ε > 0$ , il existe un entier $N (ε)$ tel que pour tous p, q>N, on a : $d (x p, x q) < ε$ . Si $ε$ est un réel standard, le principe de transfert permet d'imposer à $N (ε)$ d'être un entier standard car la suite x est standard. Or tout entier naturel non standard est strictement plus grand que tout entier naturel standard. Donc, si p et q sont des entiers non standards, ils sont plus grands que tous les $N (ε)$ . De suite, $d (x p, x q)$ est strictement inférieurs à tous les réels standards strictement positifs ; c'est donc un infiniment petit.

Réciproquement, supposons que pour tous entiers non standards p et q, le réel $d (x p, x q)$ est un infiniment petit. Fixons dans un premier temps N un entier non standard. Tout entier plus grand que N est aussi non standard. Soit $ε > 0$ un réel standard. Alors pour p et q>N, on a : $d (x p, x q) < ε$ . De fait, l'assertion suivante :
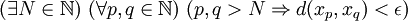
$(\exists N\in \mathbb N)\; (\forall p,q\in \mathbb N)\; (p,q>N\Rightarrow d(x_p,x_q)<\epsilon)$
est vérifiée pour tout réel standard strictement positif $ε$ . Par principe de transfert, elle est vérifiée pour tout $ε > 0$ , ce qui signifie exactement que x est de Cauchy.

Suite de Cauchy dans un espace uniforme

Définitions

Dans un espace uniforme, une suite $(x n)$ est dite de Cauchy lorsque pour tout écart continu d sur X, il existe un entier naturel N tel que pour tout $p, q > N$ , on a : $d (x p, x q) < 1$ .

Une famille (x_α) dans un espace uniforme X est une famille de Cauchy si pour tout voisinage V il existe un nombre α₀ tel que pour tous α, β > α₀, le couple (x_α, x_β) soit dans V².

Dans des exemples pratiques :

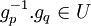Dans un groupe topologique G, une suite $(g n)$ est dite de Cauchy lorsque, pour tout voisinage V de l'élément neutre, il existe N tel que pour tous $p, q > N$ on a : $g_p^{-1}.g_q\in U$ .

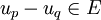Dans un espace vectoriel topologique localement convexe E, une suite de vecteurs $(u n)$ est dite de Cauchy lorsque pour tout voisinage convexe V de 0, il existe un entier naturel N tel que pour tous p, q>N on a : $u_p-u_q\in E$ .

Voir aussi

Filtre de Cauchy

Espace complet

Coupure de Dedekind

Construction des nombres réels

Notes et références

Notes

Références

Jean Dieudonné, Eléments d'analyse, t. I : Fondements de l'analyse moderne [détail des éditions]

Portail des mathématiques

Ce document provient de « Suite de Cauchy ».

Catégories : Espace métrique | Suite

Contenu soumis à la licence CC-BY-SA. Source : Article Suites de Cauchy de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Suites de cauchy — Suite de Cauchy Pour les articles homonymes, voir Cauchy. Augustin Louis Cauchy En analyse mathématique, une suite de Cauchy est une … Wikipédia en Français
Cauchy — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Cette page d’homonymie répertorie des personnes (réelles ou fictives) partageant un même patronyme. Patronyme Augustin Louis Cauchy (1789 1857),… … Wikipédia en Français
Suite de Cauchy — Pour les articles homonymes, voir Cauchy. Augustin Louis Cauchy En analyse mathématique, une suite de Cauchy est une suite de réels, de complexes, de points d … Wikipédia en Français
Suite de cauchy — Pour les articles homonymes, voir Cauchy. Augustin Louis Cauchy En analyse mathématique, une suite de Cauchy est une … Wikipédia en Français
Augustin Louis Cauchy — Pour les articles homonymes, voir Cauchy. Augustin Louis Cauchy Cauchy vers 1840. Lithographie de Zéphirin Belliard d après une peinture de Jean Roller … Wikipédia en Français
Limites de suites — Limite de suite De manière intuitive, la limite d une suite est l élément dont les termes de la suite se rapprochent quand les indices deviennent très grands. Cette définition intuitive n est guère exploitable car il faudrait pouvoir définir le… … Wikipédia en Français
Critère de Cauchy — Pour les articles homonymes, voir Cauchy. En mathématiques et en topologie, le critère de Cauchy, ainsi nommé en l’honneur du mathématicien français Augustin Louis Cauchy, est une condition se rapportant à la convergence des suites dans un espace … Wikipédia en Français
Construction des nombres réels — En mathématiques, il existe différentes constructions des nombres réels, dont les deux plus connues sont les coupures de Dedekind, les suites de Cauchy. Sommaire 1 Construction intuitive à partir des nombres décimaux 2 Construction par les… … Wikipédia en Français
MÉTRIQUES (ESPACES) — La notion d’espace métrique, introduite en 1906 par M. Fréchet et développée peu après par F. Hausdorff, est directement issue d’une analyse des principales propriétés de la distance usuelle. L’extension aux espaces métriques des propriétés de… … Encyclopédie Universelle
Construction Des Nombres Réels — Il existe différentes constructions des nombres réels, dont les deux plus rigoureuses sont les coupures de Dedekind, les suites de Cauchy. Sommaire 1 Construction intuitive à partir des nombres décimaux 2 Construction par les coupures de Dedekind … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Suites de Cauchy

Suite de Cauchy

Sommaire

Suite réelle ou complexe de Cauchy

Suite de Cauchy dans un espace métrique

Définition

Propriétés

Approche non standard

Suite de Cauchy dans un espace uniforme

Définitions

Voir aussi

Notes et références

Notes

Références

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Suites de Cauchy

Suite de Cauchy

Sommaire

Suite réelle ou complexe de Cauchy

Suite de Cauchy dans un espace métrique

Définition

Propriétés

Approche non standard

Suite de Cauchy dans un espace uniforme

Définitions

Voir aussi

Notes et références

Notes

Références

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link