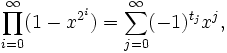Suite de prouhet-thue-morse

Suite de Prouhet-Thue-Morse

En mathématiques et ses applications, la suite de Prouhet-Thue-Morse (appelé souvent suite de Thue-Morse chez les anglo-saxons) est une certaine suite binaire. Elle commence par :

0 1 10 1001 10010110 1001011001101001... (Les espaces ne sont là que pour la compréhension visuelle permettant de construire tous les termes alors que la suite est à valeurs dans F = {0,1}.

Sommaire

1 Définition
- 1.1 Relation de récurrence
- 1.2 Un produit infini
2 Histoire
3 Propriétés
4 Notes et références
5 voir aussi
6 Liens externes

Définition

Il y a plusieurs manières équivalentes de définir cette suite.

Relation de récurrence

La suite de Prouhet-Thue-Morse est la suite $t n$ qui satisfait $t 0 = 0$ et

t 2 n = t n

t 2 n + 1 = 1 - t n

pour tous les entiers naturels n.

Un produit infini

La suite peut être aussi définie par:

$\prod_{i=0}^{\infty} (1 - x^{2^{i}}) = \sum_{j=0}^{\infty} (-1)^{t_j} x^{j} \mbox{,} \!$

Histoire

La suite de Prouhet-Thue-Morse a été découverte pour la première fois par le mathématicien français P. Prouhet en 1859, qui l'a appliquée à la théorie des nombres. Cependant, Prouhet n'a pas mentionné la suite explicitement.

Le Norvégien Axel Thue l'a employée pour établir l'étude de la combinatoire des mots en 1906. Parce que Thue a écrit seulement en norvégien, ses publications étaient inconnues ; la suite a atteint la connaissance mondiale avec les publications de Marston Morse de 1859 à 1921, quand Morse l'a utilisée pour la géométrie différentielle.

La suite a été découverte indépendamment plusieurs fois, pas toujours par des mathématiciens professionnels. Par exemple, Max Euwe, un joueur d'échecs et professeur de mathématiques, l'a découverte en 1929 pour une application aux échecs, prouvant, par ce biais, qu'il existe des parties infinies ne comportant pas de répétition des trois mêmes coups.

Propriétés

Le nombre réel correspondant (0.1101001...) est un nombre transcendant.
Aucune séquence interne consécutive de chiffres n'est répétée trois fois dans la suite : elle est dit sans cube.

Notes et références

Des mots magiques infinis, J.-P. Delahaye, Pour la science, n°347, sept 2006, p90-95

voir aussi

Liens externes

The Ubiquitous Prouhet-Thue-Morse Sequence. Allouche, J.-P.; Shallit, J. O. Quelques applications et histoire
MathWorld: Thue-Morse Sequence. Quelques autres applications

Ce document provient de « Suite de Prouhet-Thue-Morse ».

Catégorie : Suite d'entiers

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Suite de prouhet-thue-morse de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Suite de Prouhet-Thue-Morse — En mathématiques, en informatique théorique, en combinatoire des mots et ses applications, la suite de Thue Morse (appelée souvent suite de Prouhet Thue Morse chez les francophones) est une suite binaire. Elle commence par : t =… … Wikipédia en Français
Suite Prouhet-Thue-Morse — Suite de Prouhet Thue Morse En mathématiques et ses applications, la suite de Prouhet Thue Morse (appelé souvent suite de Thue Morse chez les anglo saxons) est une certaine suite binaire. Elle commence par : 0 1 10 1001 10010110… … Wikipédia en Français
Constante De Prouhet-Thue-Morse — En mathématiques et dans ses applications, la constante de Prouhet Thue Morse est le nombre dont le développement binaire est la suite de Prouhet Thue Morse. C’est à dire, où ti est la suite de Prouhet Thue Morse. La série génératrice pour ti est … Wikipédia en Français
Constante de prouhet-thue-morse — En mathématiques et dans ses applications, la constante de Prouhet Thue Morse est le nombre dont le développement binaire est la suite de Prouhet Thue Morse. C’est à dire, où ti est la suite de Prouhet Thue Morse. La série génératrice pour ti est … Wikipédia en Français
Constante de Prouhet-Thue-Morse — En mathématiques et dans ses applications, la constante de Prouhet Thue Morse est le nombre dont le développement binaire est la suite de Prouhet Thue Morse. C’est à dire, où ti est la suite de Prouhet Thue Morse. La série génératrice pour ti est … Wikipédia en Français
Morse — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Un morse. Le morse est un mammifère marin, mais l appellation peu … Wikipédia en Français
Axel Thue — (19 février 1863 7 mars 1922) est un mathématicien norvégien. En 1909, il publia un article important avec le théorème suivant, essentiel pour l étude des équations diophantiennes : Théorème Si f(x;y) est un polynôme homogène à coefficients… … Wikipédia en Français
Marston Morse — Pour les articles homonymes, voir Marston et Morse. H. C. Marston Morse Marston Morse en 1965 (collection du MFO) Naissance … Wikipédia en Français
Morses — Morse Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Le morse est un mammifère marin. Le nom Morse peut faire référence à : Patronymes Anthony P. Morse, mathématicien ; voir notamment la… … Wikipédia en Français
Combinatoire des mots — Construction de la suite de Prouhet Thue Morse. La combinatoire des mots est une branche des mathématiques et de l informatique théorique qui applique l analyse combinatoire aux mots finis ou infinis. Cette branche s est développée à partir de… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Suite de prouhet-thue-morse