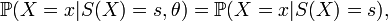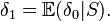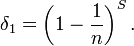- Stastiques
-
Statistique
 Attention :
Une statistique est une quantité calculée à partir d'un certain nombre d'observations. On distingue donc en mathématique la statistique qui est le domaine des mathématiques et une statistique qui est le principal objet de l'étude statistique. Cette page ne concerne donc que les principaux types de statistiques, l'usage qu'il en est fait ainsi que leur principales propriétés. Pour un article plus général sur la statistique consultez la page statistiques.
Attention :
Une statistique est une quantité calculée à partir d'un certain nombre d'observations. On distingue donc en mathématique la statistique qui est le domaine des mathématiques et une statistique qui est le principal objet de l'étude statistique. Cette page ne concerne donc que les principaux types de statistiques, l'usage qu'il en est fait ainsi que leur principales propriétés. Pour un article plus général sur la statistique consultez la page statistiques.Une statistique est, au premier abord, un nombre calculé à propos d'un échantillon. D'une façon générale, c'est le résultat de l'application d'une méthode statistique à un ensemble de données. Dans le calcul de la moyenne arithmétique, par exemple, l'algorithme consiste à calculer la somme de toutes les valeurs des données et à diviser par le nombre de données. La moyenne est ainsi une statistique. Pour être complet dans la description de l'utilisation d'une statistique, il faut décrire à la fois la procédure et l'ensemble de données.
De façon formelle bien que cela soit rarement utilisé une statistique est une variable aléatoire d'un type particulier. C'est en effet une fonction d'un vecteur composée de plusieurs observations d'une loi. Cela permet entre autres d'étendre aux statistiques un certain nombre de résultats sur les variables aléatoires entre autres le caractère indépendant de deux statistiques ou calculer des densités de statistiques.
Parmi les statistiques un certain nombre ont des propriétés particulières qui servent entre autres en Inférence statistique pour l'estimation statistique. Les estimateurs servent, comme leur nom l'indique, à estimer des paramètres statistiques. L'optimisation de ces estimateurs peut également faire intervenir des statistiques auxiliaires vérifiant certaines propriétés et qui permettent de faire converger plus vite ces estimateurs.
Sommaire
Estimateurs
En statistique inférentielle, un estimateur est une valeur calculée sur un échantillon et que l'on espère être une bonne évaluation de la valeur que l'on aurait calculée sur la population totale. On cherche à ce qu'un estimateur soit sans biais, convergent, efficace et robuste.
Principales propriétés souhaitables
Si
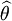 est un estimateur de θ on dit qu'il est:
est un estimateur de θ on dit qu'il est:- Convergent si:
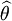 tend en probabilité vers θ quand le nombre d'observations augmente. Plus le nombre d'observations est grand et plus l'on se rapproche de la vraie valeur. Cette propriété d'un estimateur est essentielle si l'on veut pouvoir estimer avec grande précision le paramètre θ. En effet, si c'est le cas, pour augmenter la précision de l'estimateur, il suffira d'effectuer plus de mesures.
tend en probabilité vers θ quand le nombre d'observations augmente. Plus le nombre d'observations est grand et plus l'on se rapproche de la vraie valeur. Cette propriété d'un estimateur est essentielle si l'on veut pouvoir estimer avec grande précision le paramètre θ. En effet, si c'est le cas, pour augmenter la précision de l'estimateur, il suffira d'effectuer plus de mesures. - Sans biais si:
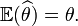 On peut voir un estimateur sans biais comme un estimateur pour lequel on ne fait pas d'erreur systématique pour une taille d'échantillon donnée. À contrario pour un estimateur qui aurait un biais il pourrait par exemple exister des valeurs du paramètre θ pour lesquelles on sur estimerait ou sous estimerait de façon systématique la grandeur que l'on cherche à évaluer. C'est pour qu'il soit sans biais que l'on estime d'ordinaire la variance quand on a n observations par
On peut voir un estimateur sans biais comme un estimateur pour lequel on ne fait pas d'erreur systématique pour une taille d'échantillon donnée. À contrario pour un estimateur qui aurait un biais il pourrait par exemple exister des valeurs du paramètre θ pour lesquelles on sur estimerait ou sous estimerait de façon systématique la grandeur que l'on cherche à évaluer. C'est pour qu'il soit sans biais que l'on estime d'ordinaire la variance quand on a n observations par 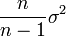 et non par σ2 par exemple.
et non par σ2 par exemple.
Ces deux propriétés sont essentielles et en règle générale on considère que tout estimateur devrait au moins vérifier ces deux propriétés pour qu'on puisse le considérer comme suffisamment précis. On peut de plus vouloir qu'un estimateur soit efficace (c'est-à-dire que l'estimation qu'il fournit varie le moins possible autour de la valeur à estimer) ou robuste (c'est-à-dire qu'il soit peu sensible aux variations d'une mesure sur les n). Ces deux propriétés sont détaillées plus bas dans les sections Optimisation d'estimateur et Robustesse.
Statistique exhaustive et information
Une propriété intéressante qu'une statistique peut avoir est son caractère exhaustif. Une statistique S est dite exhaustive si la probabilité conditionnelle d'observer X sachant S(X) est indépendante de θ. Cela peut se traduire par la formule suivante:
Cette définition n'étant pas forcément très simple à manier en pratique on préfère souvent utiliser la caractérisation de factorisation des statistiques exhaustives. Ces statistiques exhaustives sont particulièrement importantes car fournissent toute l'information qu'il est possible de récupérer sur le paramètre à partir d'une série d'observations. Une statistique exhaustive apporte donc autant d'information que l'ensemble du vecteur des observations x et l'on ne peut pas récupérer plus d'information que celle contenue dans une statistique exhaustive. Cela se formalise grâce à l'information de Fisher. Si IS est l'information de Fisher apportée par une statistique S et I l'information du modèle:
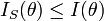
Avec un cas d'égalité uniquement dans le cas d'une statistique exhaustive. Pour le cas d'un modèle à un seul paramètre cette inégalité est une inégalité classique. Pour le cas des modèles multiparamétrés cette inégalité est une inégalité au sens de la relation d'ordre partielle introduite par:
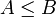 si B-A est une matrice symétrique positive.
si B-A est une matrice symétrique positive.Optimisation d'estimateurs
L'optimisation d'estimateurs peut se faire grâce à l'usage de statistiques exhaustives. Une méthode possible pour trouver de "bons" estimateurs est de prendre un premier estimateur sans biais de la valeur à estimer sans trop chercher à l'optimiser. Ensuite on optimise cet estimateur en se servant de statistiques exhaustives.
Cette méthode repose principalement sur deux théorèmes : le théorème de Rao-Blackwell qui fournit un deuxième estimateur de meilleur qualité appelé estimateur augmenté et le théorème de Lehman-Scheffer qui donne des conditions suffisantes pour que cet estimateur soit optimal.
Estimateurs augmentés et Théorème de Rao-Blackwell
Si δ est un estimateur sans biais et S une statistique exhaustive alors l'estimateur augmenté
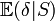 a une variance plus faible que l'espérance de départ et est également sans biais. L'estimateur augmenté est donc toujours plus précis que l'estimateur initial si on l'augmente d'une statistique exhaustive.
a une variance plus faible que l'espérance de départ et est également sans biais. L'estimateur augmenté est donc toujours plus précis que l'estimateur initial si on l'augmente d'une statistique exhaustive.Dans le cas multiparamétrique où l'estimateur et le paramètre sont de dimension supérieure 1, on considère la matrice de variance-covariance. L'erreur quadratique du nouvel estimateur est toujours plus faible que celui de l'ancien estimateur et ce quelle que soit la norme utilisée. Même si les différentes composantes ne sont pas normées de la même façon l'estimateur augmenté est toujours préférable.
Exemple
On considère donc n variables aléatoires Xi distribués selon des lois de Poisson de paramètre λ et l'on cherche à estimer e − λ. On peut montrer assez facilement en considérant le critère de factorisation que
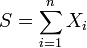 est une statistique exhaustive. Pour montrer l'intérêt de ce théorème, on prend un estimateur très grossier de e − λ: δ0 = δ(X1,0) qui vaut 1 si X1 = 0 et 0 sinon. Cet estimateur ne prend en compte qu'une seule valeur de X alors qu'on en dispose de n et il ne donne pour résultat que 0 ou 1 alors que la valeur de e − λ appartient à l'intervalle ]0,1] et ne vaut sans doute pas 1. (si c'était le cas Xi vaudrait 0 de façon déterministe et on s'en serait aperçu en regardant les données). Pourtant malgré la grossièreté de cet estimateur, l'estimateur obtenu est très bon et on peut même montrer qu'il est optimal. L'estimateur augmenté vaut :
est une statistique exhaustive. Pour montrer l'intérêt de ce théorème, on prend un estimateur très grossier de e − λ: δ0 = δ(X1,0) qui vaut 1 si X1 = 0 et 0 sinon. Cet estimateur ne prend en compte qu'une seule valeur de X alors qu'on en dispose de n et il ne donne pour résultat que 0 ou 1 alors que la valeur de e − λ appartient à l'intervalle ]0,1] et ne vaut sans doute pas 1. (si c'était le cas Xi vaudrait 0 de façon déterministe et on s'en serait aperçu en regardant les données). Pourtant malgré la grossièreté de cet estimateur, l'estimateur obtenu est très bon et on peut même montrer qu'il est optimal. L'estimateur augmenté vaut :On peut montrer que:
Détails du calcul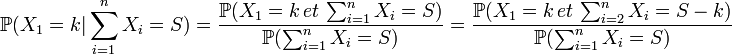
Et avec l'indépendance de Xi:
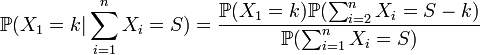
Si Xi suit une loi de poisson de paramètre λ alors la fonction génératrice vaut
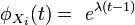 . Avec les propriétés de la fonction génératrice on en déduit que la somme de n variables suivant des lois de poisson de paramètre λ est une loi de Poisson de paramètre nλ. On en déduit les probabilités et
. Avec les propriétés de la fonction génératrice on en déduit que la somme de n variables suivant des lois de poisson de paramètre λ est une loi de Poisson de paramètre nλ. On en déduit les probabilités et 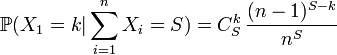 X1 suis une loi binomiale B(S, 1/n). La valeur en k=0 nous donne l'estimateur δ1
X1 suis une loi binomiale B(S, 1/n). La valeur en k=0 nous donne l'estimateur δ1δ1 est tout comme de δ0 un estimateur de e − λ mais à l'avantage d'être beaucoup plus précis grâce à l'application du théorème de Rao–Blackwell. En fait, on montre avec Théorème de Lehman Scheffé qu'il est même optimal.
On remarquera entre autres que
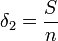 est un estimateur optimal de λ (cela se montre de la même manière) mais que l'estimateur pour e − λ est différent de
est un estimateur optimal de λ (cela se montre de la même manière) mais que l'estimateur pour e − λ est différent de 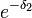 . En fait, on peut même montrer que bien que
. En fait, on peut même montrer que bien que 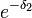 soit un estimateur convergent de e − λ c'est un estimateur de relativement mauvaise qualité car il est biaisé et qu'en l'estimant de la sorte on fait une erreur systématique sur l'estimation. De façon générale, il peut être intéressant pour estimer f(λ) de construire un estimateur spécifique plutôt que de calculer la valeur prise par f par l'estimateur de λ.
soit un estimateur convergent de e − λ c'est un estimateur de relativement mauvaise qualité car il est biaisé et qu'en l'estimant de la sorte on fait une erreur systématique sur l'estimation. De façon générale, il peut être intéressant pour estimer f(λ) de construire un estimateur spécifique plutôt que de calculer la valeur prise par f par l'estimateur de λ.Statistique complète et Théorème de Lehman Scheffé
On dit qu'une statistique est complète (on dit parfois totale) si :
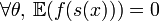 implique f=0 presque partout.
implique f=0 presque partout.Le théorème de Lehman-Scheffé a une importance particulière en statistiques puisqu'il permet de trouver des estimateurs optimaux qui ne peuvent pas être améliorés en termes de précision car ils atteignent la borne FDCR. De tels estimateurs n'existent pas forcément mais si l'on dispose d'une statistique qui soit à la fois complète et totale et d'un estimateur δ qui soit sans biais alors l'estimateur augmenté
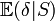 est optimal et l'on ne peut pas trouver de meilleur estimateur.
est optimal et l'on ne peut pas trouver de meilleur estimateur.Exemple
Montrons par exemple que pour une loi exponentielle de paramètres λ la moyenne des observations est le meilleure estimateur possible pour λ. Si l'on a un vecteur des observations X de taille n avec les Xi de loi exponentielle (λ,σ) on commence par montrer que
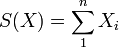 est une statistique exhaustive et complète.
est une statistique exhaustive et complète.Pour montrer que cette statistique est exhaustive cela se fait relativement simplement grâce au théorème de factorisation. Pour montrer le fait que cette statistique est complète il faut utiliser l'injectivité de la transformée de Laplace.
Détails du calculPour montrer que c'est bien une statistique complète il faut vérifier que:
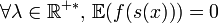 implique bien que f=0 presque partout. Avec la définition d'une loi gamma s(x) suit une loi gamma de paramètre (n,λ) on a donc en remplaçant par la densité d'une loi gamma:
implique bien que f=0 presque partout. Avec la définition d'une loi gamma s(x) suit une loi gamma de paramètre (n,λ) on a donc en remplaçant par la densité d'une loi gamma: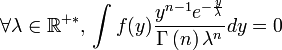 d'où:
d'où:  Par injectivité de la transformée de Laplace on en déduit donc que f(y)yn − 1 = 0 presque partout puis que f(y)=0 presque partout donc la statistique est bien complète.
Par injectivité de la transformée de Laplace on en déduit donc que f(y)yn − 1 = 0 presque partout puis que f(y)=0 presque partout donc la statistique est bien complète.Une fois montré que la statistique S est à la fois complète et exhaustive l'estimateur de la moyenne
 étant égal à l'estimateur augmenté
étant égal à l'estimateur augmenté 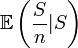 on en déduit immédiatement grâce au théorème de Lehman Scheffé que cet estimateur est optimal au sens où il atteint la borne FDCR et que l'on ne peut en trouver de meilleur. L'estimateur de la moyenne est l'estimateur le plus précis que l'on puisse trouver pour le paramètre d'une loi exponentielle.
on en déduit immédiatement grâce au théorème de Lehman Scheffé que cet estimateur est optimal au sens où il atteint la borne FDCR et que l'on ne peut en trouver de meilleur. L'estimateur de la moyenne est l'estimateur le plus précis que l'on puisse trouver pour le paramètre d'une loi exponentielle.Statistique robuste
Voir aussi
- Statistique
- Statistique mathématique
- Statistique (mathématiques élémentaires)
- Statistique descriptive
- Inférence statistique
Références
- A. Montfort Cours de statistique mathématique, 1982, Economica. Paris.
Liens externes
- Jean-Pierre Favre, Mathématiques de gestion, Digilex, 2009, ISBN : 978-2-940404-01-8
- P. Druilhet [1] Cours de statistique interférentielle.
- Exemple de représentation dynamique de statistiques (par compteurs, pour différents types de statistiques, dont démographiques, sanitaires, environnementales)
- Page de l'artiste Chris Jordan, qui produit des œuvres cherchant à rendre visuellement perceptible des statistiques portant sur de grands nombres.
- Portail des probabilités et des statistiques
Catégorie : Statistiques - Convergent si:
Wikimedia Foundation. 2010.