- Son résultant
-
En acoustique, un son résultant (appelé aussi un son différentiel ou concomitant) est un son produit par deux autres par le phénomène de battement[1].
Il s'agit d'un troisième son (ou une note de musique), parfaitement audible, bien que notablement plus faible, produit par l'interférence des deux premiers, et correspondant à leur différence acoustique.
Sommaire
Explication
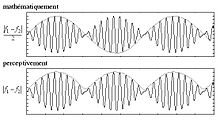
Lorsque l'oreille entend simultanément deux sons de fréquences proches, elle perçoit une fréquence moyenne agrémentée d'un battement dont la fréquence est la différence de fréquence des deux sons. On entend la différence de fréquence des deux sons, et non pas la moitié de la différence. Si, mathématiquement, l'enveloppe du battement est la demi-différence et l'intérieur la demi-somme, l'oreille perd la phase : quand l'enveloppe est négative et décroît algébriquement, l'oreille l'entend positive et croissante comme dans la demi-alternance précédente. Il y a donc doublement de la fréquence perçue au niveau de l'enveloppe du battement. Pour une tierce majeure [do, mi], le battement se produit entre l'harmonique 5 du do et l'harmonique 4 du mi.
Fichier audio Battements et son résultant (deux embouchures de flûte à bec). À écouter fort et au casque (info)
 Des problèmes pour écouter le fichier ?
Des problèmes pour écouter le fichier ?Lorsque ces deux sons ont des fréquences nettement différentes, l'oreille perçoit alors distinctement chacun de ces deux sons, mais l'ensemble est agrémenté d'un troisième son dont la fréquence est la différence de fréquence des deux sons : ce troisième son s'appelle le son résultant, ou son différentiel. Pour bien entendre de quoi il s'agit, il suffit de porter à la bouche deux embouchures identiques de flûtes à bec et d'abaisser la fréquence de l'un des deux sons en obstruant partiellement la sortie avec un doigt. Pour une obstruction à peine sensible, on produit des battements. En augmentant l'obstruction, la fréquence des battements augmente jusqu'à ce qu'elle entre dans le domaine audible. On entend alors un bourdonnement dans l'extrême grave, dont la fréquence augmente au fur et à mesure que la fréquence produite par l'embouchure obstruée diminue. Le son différentiel devient très présent dès que sa fréquence le situe dans les tessitures musicales habituelles.
Utilisation en organologie
Par exemple, un intervalle de tierce pure, de rapport 5/4, va émettre un son résultant de 5/4-1=1/4, soit la note du bas, mais deux octaves en dessous. Par exemple do4-mi4 permettent d'entendre un do2, très ténu. Pour faire faire cette expérience, il vaut mieux utiliser des instruments timbrés et aigus : la flûte à bec est un parfait moyen de mettre ce phénomène en évidence. Toutefois, il faut que le souffle des joueurs soit parfaitement stable et la précision de justesse grande, le son résultant évoluant très rapidement selon la justesse relative des deux notes.
Ce phénomène a été utilisé en particulier dans les orgues mécaniques (limonaires), afin de pallier l'absence, par souci d'économie, de certains tuyaux de basse. On entend vraiment un tuyau qui n'existe pas, un tuyau virtuel, en quelque sorte. Il est aussi utilisé dans certains registres de grands orgues.
Il s'agit du même phénomène d'interférence que le battement, mais d'une fréquence plus élevée, audible alors en tant que son musical, et non plus en tant que variation périodique d'amplitude (voir Justesse des tierces).
Diplophonie
Ce phénomène est connu en oto-rhino-laryngologie sous le nom de "voix bitonale" ou de "diplophonie": un sujet dont une des deux cordes vocales est dysfonctionnelle produit une voix dont le fondamental est "double" . On a émis l'hypothèse que le même phénomène pourrait survenir a minima dans certaines conditions physiologiques : par exemple lorsqu'un sujet qui contrôle habituellement sa voix par l'écoute dominante de l'oreille droite devrait - pour une raison quelconque - utiliser préférentiellement son autre oreille.
Histoire
Le phénomène de son différentiel a été découvert indépendamment par plusieurs théoriciens :
- Georg Sorge en 1745[1],
- Jean Baptiste Romieu en 1751[1],
- Giuseppe Tartini en 1754[1].
Notes et références
- Jacques Chailley, Expliquer l'harmonie ?, Editions Rencontre, 1967 (ISBN 2-7384-3964-0), Edition L'Harmattan, collection Les Introuvables, 2006, p. 64
Annexes
Liens externes
Articles connexes
Wikimedia Foundation. 2010.