Algèbre stellaire

Une algèbre stellaire ou C*-algèbre est l'objet d'étude de la géométrie non commutative. Cette notion a été formalisée en 1943 par Gelfand et Segal. Les algèbres stellaires sont centrales dans l'étude des représentations unitaires de groupes localement compacts.

Sommaire 1 Définition 2 Exemples de C*-algèbres 3 Spectre des éléments d'une C*-algèbre 4 Classification des C*-algèbres commutatives 5 Le calcul fonctionnel continu 6 La construction GNS 7 Remarques 8 Voir aussi

Définition

Une algèbre stellaire A est une algèbre de Banach complexe

• munie d'une involution

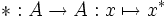
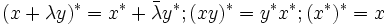
pour tout x, y dans A, λ un nombre complexe

• telle que la norme et l'involutions sont liées par pour tout x dans A.

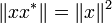
Par la seconde condition, 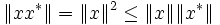et donc, par symétrie, on obtient :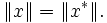

Un *-homomorphisme est un homomorphisme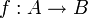 vérifiant:

f(x ^* ) = f(x) ^* .

Cette condition implique que f est une isométrie (et donc en particulier injective et continue). Si f est bijective, son inverse est un *-homomorphisme ; auquel cas, f est appelée *-isomorphisme.

Exemples de C*-algèbres

• Soit X un espace compact, alors C(X), l'algèbre des fonctions continues sur X à valeurs complexes est une C*-algèbre commutative avec unité.
• Si X est localement compact, mais non compact, C₀(X), l'algèbre des fonctions continues sur X qui tendent vers zéro à l'infini est une C*-algèbre commutative sans unité. (L'existence d'une approximation de l'unité dans C₀(X) résulte du théorème de Tietze-Urysohn).
• Si H désigne un espace de Hilbert, toute sous-algèbre fermée pour la norme d'opérateurs de l'algèbre des opérateurs bornés sur H est une C*-algèbre, a priori non commutative.

Spectre des éléments d'une C*-algèbre

Tout comme pour les opérateurs dans un espace de Hilbert, on peut définir le spectre des éléments d'une C*-algèbre. Le spectre de x est l'ensemble: 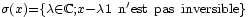. Cet ensemble suppose que l'algèbre contenant x ait une unité. Cependant, si ce n'est pas le cas, on peut toujours définir le spectre en adjoignant une unité à l'algèbre. (détailler la méthode pour adjoindre l'élément unité ?)

Classification des C*-algèbres commutatives

Si A est une C*-algèbre commutative, la transformée de Gelfand est un isomorphisme entre A et C₀(X), où X est le spectre de A (c'est-à-dire l'espace des caractères de A). C'est le théorème de représentation de Gelfand. X est localement compact, et même compact si A a une unité.

Le calcul fonctionnel continu

Si x est un élément normal d'une C*-algèbre A (c’est-à-dire commutant à son adjoint), alors il existe un *-isomorphisme isométrique entre l'algèbre des fonctions continues sur le spectre de x et la sous-C*-algèbre de A engendrée par x et 1. Autrement dit, pour tout f continue sur σ(x), on peut définir f(x) de manière unique, comme un élément de A. Ce calcul fonctionnel prolonge le calcul fonctionnel polynomial, et σ(f(x)) = f(σ(x)) (théorème spectral).

La construction GNS

On doit à Gelfand, Naimark et Segal la construction d'un isomorphisme isométrique (ou représentation fidèle) entre toute C*-algèbre, et une sous-algèbre fermée de l'algèbre des opérateurs sur un certain espace de Hilbert H (que l'on construit en même temps que l'isomorphisme). La théorie des C*algèbre peut donc se ramener à la théorie des opérateurs sur les espaces de Hilbert.

Remarques

Le fait que les C*-algèbres commutatives sont des algèbres de fonctions permet de penser la théorie des C*-algèbre comme une théorie des fonctions non commutatives. Mais comme l'étude des fonctions continues sur un espace compact est équivalente à l'étude de la topologie de cet espace (par théorème de Banach-Stone), on donne plus volontiers à l'étude des C^*-algèbres le nom de topologie non commutative.

Voir aussi

• Analyse fonctionnelle : L'étude des C*-algèbres, notamment par son aspect spectral, est une branche de l'analyse fonctionnelle.
• Algèbre des opérateurs : L'étude des C*-algèbre peut se ramener à l'étude des opérateurs sur un hilbert par la construction GNS.
• K-théorie : Les outils de K-théorie, développés d'abord pour l'étude des fibrés, peuvent être adaptés à l'étude des C*-algèbres. On obtient en quelque sorte une topologie algébrique non commutative.
• Géométrie non commutative : Ce domaine cherche des analogues aux notions de la géométrie différentielle (connexions, cohomologie ...) dans le cadre non commutatif des algèbres d'opérateurs.

• Portail des mathématiques