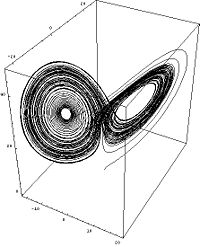
Attracteur Étrange

Attracteur Étrange

Système dynamique de Lorenz

Pour consulter un article plus général, voir : théorie du chaos.

En 1963, le météorologue Edward Lorenz est le premier à mettre en évidence le caractère vraisemblablement chaotique de la météorologie.

Sommaire

Modèle de Lorenz

Mathématiquement, le couplage de l'atmosphère avec l'océan est décrit par le système d'équations aux dérivées partielles couplées de Navier-Stokes de la mécanique des fluides. Ce système d'équations était beaucoup trop compliqué à résoudre numériquement pour les premiers ordinateurs existant au temps de Lorenz. Celui-ci eut donc l'idée de chercher un modèle très simplifié de ces équations pour étudier une situation physique particulière : le phénomène de convection de Rayleigh-Bénard. Il aboutit alors à un système dynamique différentiel possédant seulement trois degrés de liberté, beaucoup plus simple à intégrer numériquement que les équations de départ.

Système dynamique différentiel de Lorenz

Ce système différentiel s'écrit :

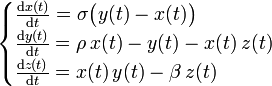
\begin{cases} \frac{\mathrm{d}x(t)}{\mathrm{d}t}=\sigma \bigl( y(t) - x(t) \bigr)\\ \frac{\mathrm{d}y(t)}{\mathrm{d}t}=\rho \, x(t) - y(t) - x(t) \, z(t)\\ \frac{\mathrm{d}z(t)}{\mathrm{d}t} =x(t) \, y(t) - \beta \, z(t) \end{cases}

Dans ces équations, σ,ρ – respectivement le nombre de Prandtl et le rapport du nombre de Rayleigh sur un Rayleigh critique – et β sont trois paramètres réels.

x(t) est proportionnel à l'intensité du mouvement de convection, y(t) est proportionnel à la différence de température entre les courants ascendants et descendants, et z(t) est proportionnel à l'écart du profil de température vertical par rapport à un profil linéaire (Lorenz 1963, p. 135).

Points fixes

Les points fixes du système sont les solutions (x,y,z) constantes du système différentiel. Il en existe trois :

  • le point fixe (0, 0, 0), qui existe quelles que soient les valeurs des paramètres réels σ,ρ et β.
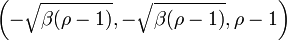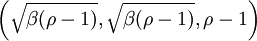  • les deux points fixes symétriques : \left( - \sqrt{\beta(\rho - 1)},-\sqrt{\beta( \rho - 1)}, \rho - 1\right) et : \left( \sqrt{\beta( \rho - 1)},\sqrt{\beta( \rho - 1)}, \rho - 1 \right), qui n'existent que lorsque ρ > 1.

Attracteur étrange

Article détaillé : attracteur de Lorenz.
Attracteur étrange de Lorenz

Lorsque les paramètres σ,ρ et β prennent les valeurs suivantes :σ = 10, ρ = 28 et β = 8 / 3, le système dynamique différentiel de Lorenz présente un superbe attracteur étrange en forme d'ailes de papillon, représenté sur la figure ci-contre.

Pour presque toutes les conditions initiales (différentes de celles des points fixes), l'orbite du système se promène sur l'attracteur, la trajectoire commençant par s'enrouler sur une aile, puis sautant d'une aile à l'autre pour commencer à s'enrouler sur l'autre aile, et ainsi de suite, de façon apparemment erratique.

Articles connexes

Bibliographie

  • (en) W. Tucker, « A Rigorous ODE Solver and Smale's 14th Problem », dans Found. Comp. Math., vol. 2, 2002, p. 53–117 [texte intégral] .
  • Portail des mathématiques Portail des mathématiques
  • Portail de la physique Portail de la physique
Ce document provient de « Syst%C3%A8me dynamique de Lorenz ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Attracteur Étrange de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Attracteur étrange — Système dynamique de Lorenz Pour consulter un article plus général, voir : théorie du chaos. En 1963, le météorologue Edward Lorenz est le premier à mettre en évidence le caractère vraisemblablement chaotique de la météorologie. Sommaire 1… …   Wikipédia en Français

  • Attracteur De Hénon — pour a = 1,4 etb = 0,3 L attracteur de Hénon est un système dynamique à temps discret. C est l un des systèmes dynamiques ayant un comportement chaotique les plus étudiés. L attracteur de Hénon prend tout point du plan (x, y) …   Wikipédia en Français

  • Attracteur de Henon — Attracteur de Hénon attracteur de Hénon pour a = 1,4 etb = 0,3 L attracteur de Hénon est un système dynamique à temps discret. C est l un des systèmes dynamiques ayant un comportement chaotique les plus étudiés. L attracteur de Hénon prend tout… …   Wikipédia en Français

  • Attracteur de Rossler — Attracteur de Rössler L attracteur de Rössler L attracteur de Rössler est l attracteur associé au système dynamique de Rössler, un système de 3 équations différentielles non linéaires. Ces équations différentielles définissent un système… …   Wikipédia en Français

  • Attracteur de hénon — pour a = 1,4 etb = 0,3 L attracteur de Hénon est un système dynamique à temps discret. C est l un des systèmes dynamiques ayant un comportement chaotique les plus étudiés. L attracteur de Hénon prend tout point du plan (x, y) …   Wikipédia en Français

  • Attracteur de Hénon — pour a = 1,4 etb = 0,3 L attracteur de Hénon est un système dynamique à temps discret. C est l un des systèmes dynamiques ayant un comportement chaotique les plus étudiés. L attracteur de Hénon prend tout point du plan (x, y) et lui associe… …   Wikipédia en Français

  • Attracteur De Lorentz — Attracteur de Lorenz L attracteur de Lorenz L attracteur de Lorenz, baptisé d après son découvreur Edward Lorenz, est une structure fractale correspondant au comportement à long terme de l oscillateur de Lorenz. Cet oscillateur est un système… …   Wikipédia en Français

  • Attracteur De Lorenz — L attracteur de Lorenz L attracteur de Lorenz, baptisé d après son découvreur Edward Lorenz, est une structure fractale correspondant au comportement à long terme de l oscillateur de Lorenz. Cet oscillateur est un système dynamique tridimensionel …   Wikipédia en Français

  • Attracteur de lorenz — L attracteur de Lorenz L attracteur de Lorenz, baptisé d après son découvreur Edward Lorenz, est une structure fractale correspondant au comportement à long terme de l oscillateur de Lorenz. Cet oscillateur est un système dynamique tridimensionel …   Wikipédia en Français

  • Attracteur de Lorenz — Pour consulter un article plus général, voir : théorie du chaos. L attracteur de Lorenz En 1963, le météorologue Edward Lorenz est le premier à mettre en évidence le caractère vraisemblablement chaotique de la météorologie. Le modèle de… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”