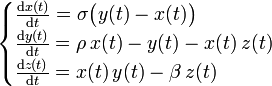Attracteur de lorenz

Attracteur de Lorenz

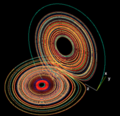
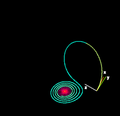
L'attracteur de Lorenz

L attracteur de Lorenz, baptisé d'après son découvreur Edward Lorenz, est une structure fractale correspondant au comportement à long terme de l'oscillateur de Lorenz. Cet oscillateur est un système dynamique tridimensionel qui engendre un comportement chaotique dans certaines conditions. L'attracteur montre comment les différentes variables du système dynamique évoluent dans le temps en une trajectoire non périodique.

Définition

L'attracteur et les équations associées ont été rendues publiques en 1963 par Edward Lorenz, qui les avait extraites d'une version simplifiée des équations de convection qui surviennent dans l'atmosphère.

Il est défini comme l'ensemble des trajectoires à long terme du système dynamique de Lorenz :

$\begin{cases} \frac{\mathrm{d}x(t)}{\mathrm{d}t}=\sigma \bigl( y(t) - x(t) \bigr)\\ \frac{\mathrm{d}y(t)}{\mathrm{d}t}=\rho \, x(t) - y(t) - x(t) \, z(t)\\ \frac{\mathrm{d}z(t)}{\mathrm{d}t} =x(t) \, y(t) - \beta \, z(t) \end{cases}$

où $σ$ est appelé nombre de Prandtl et $ρ$ est appelé nombre de Rayleigh. $σ$ , $ρ$ et $β$ sont strictement positifs, et on pose souvent $σ$ = 10, $β$ = 8/3 ; $ρ$ restant variable. Le système présente un comportement chaotique pour $ρ$ = 28.

Le modèle de Lorenz a eu des répercussions importantes sur la capacité de prédiction à long terme de l'évolution climatique et météorologique. Il est un élément important dans la théorie selon laquelle l'atmosphère des planètes et des étoiles peut comporter une grande variété de régimes quasi-périodiques et est sujette à des changements abrupts et, en apparence, aléatoires.

En 2001 Warwick Tucker prouva que pour certaines valeurs de paramètres, le système engendrait un comportement chaotique se traduisant graphiquement par un "attracteur étrange".

L'attracteur, dans ces cas, est une fractale de dimension de Hausdorff entre 2 et 3. Grassberger (1983) a estimé sa valeur à 2.06 ± 0.01 et sa dimension de corrélation à 2.05 ± 0.01.

Article détaillé : système dynamique de Lorenz.

ρ=28, σ = 10, β = 8/3

ρ=28

ρ=15

Voir aussi

Bibliographie

(en)Deterministic Nonperiodic Flow By EDWARD N. Lorenz

(en) W. Tucker, « A Rigorous ODE Solver and Smale's 14th Problem », dans Found. Comp. Math., vol. 2, 2002, p. 53–117 [texte intégral] .

Portail des mathématiques
Portail sur les sciences
Portail de la physique

Ce document provient de « Attracteur de Lorenz ».

Catégories : Système dynamique remarquable | Méthode mathématique de la physique | Ingénierie | Système

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Attracteur de lorenz de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Attracteur De Lorenz — L attracteur de Lorenz L attracteur de Lorenz, baptisé d après son découvreur Edward Lorenz, est une structure fractale correspondant au comportement à long terme de l oscillateur de Lorenz. Cet oscillateur est un système dynamique tridimensionel … Wikipédia en Français
Attracteur de Lorenz — Pour consulter un article plus général, voir : théorie du chaos. L attracteur de Lorenz En 1963, le météorologue Edward Lorenz est le premier à mettre en évidence le caractère vraisemblablement chaotique de la météorologie. Le modèle de… … Wikipédia en Français
Attracteur De Lorentz — Attracteur de Lorenz L attracteur de Lorenz L attracteur de Lorenz, baptisé d après son découvreur Edward Lorenz, est une structure fractale correspondant au comportement à long terme de l oscillateur de Lorenz. Cet oscillateur est un système… … Wikipédia en Français
Attracteur de Rossler — Attracteur de Rössler L attracteur de Rössler L attracteur de Rössler est l attracteur associé au système dynamique de Rössler, un système de 3 équations différentielles non linéaires. Ces équations différentielles définissent un système… … Wikipédia en Français
Attracteur De Hénon — pour a = 1,4 etb = 0,3 L attracteur de Hénon est un système dynamique à temps discret. C est l un des systèmes dynamiques ayant un comportement chaotique les plus étudiés. L attracteur de Hénon prend tout point du plan (x, y) … Wikipédia en Français
Attracteur de Henon — Attracteur de Hénon attracteur de Hénon pour a = 1,4 etb = 0,3 L attracteur de Hénon est un système dynamique à temps discret. C est l un des systèmes dynamiques ayant un comportement chaotique les plus étudiés. L attracteur de Hénon prend tout… … Wikipédia en Français
Attracteur de hénon — pour a = 1,4 etb = 0,3 L attracteur de Hénon est un système dynamique à temps discret. C est l un des systèmes dynamiques ayant un comportement chaotique les plus étudiés. L attracteur de Hénon prend tout point du plan (x, y) … Wikipédia en Français
Attracteur de Hénon — pour a = 1,4 etb = 0,3 L attracteur de Hénon est un système dynamique à temps discret. C est l un des systèmes dynamiques ayant un comportement chaotique les plus étudiés. L attracteur de Hénon prend tout point du plan (x, y) et lui associe… … Wikipédia en Français
Attracteur Étrange — Système dynamique de Lorenz Pour consulter un article plus général, voir : théorie du chaos. En 1963, le météorologue Edward Lorenz est le premier à mettre en évidence le caractère vraisemblablement chaotique de la météorologie. Sommaire 1… … Wikipédia en Français
Attracteur étrange — Système dynamique de Lorenz Pour consulter un article plus général, voir : théorie du chaos. En 1963, le météorologue Edward Lorenz est le premier à mettre en évidence le caractère vraisemblablement chaotique de la météorologie. Sommaire 1… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Attracteur de lorenz