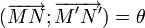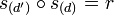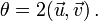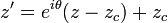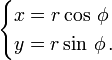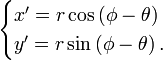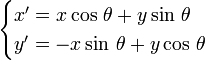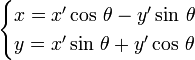Rotation (mathématiques élémentaires)

Rotation (mathématiques élémentaires)

Rotation plane

Icone math élém.jpg
Cet article fait partie de la série
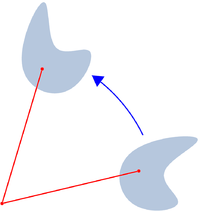
Mathématiques élémentaires
Algèbre
Logique
Arithmétique
Probabilités
Statistiques

En géométrie dans le plan, une rotation plane est une transformation qui fait tourner les figures autour d'un point et d'un certain angle. Cette transformation est une isométrie car les distances sont conservées. La figure n'a été ni déformée, ni agrandie.

La rotation fait intervenir la notion d'angle orienté ce qui fait d'elle une des transformations les moins évidentes des transformations euclidiennes.

Sommaire

Définition, propriétés et caractérisations

Définition

Image d'une figure par rotation

Définition : Dans le plan orienté, la rotation de centre C et d'angle θ est la transformation qui laisse C invariant et qui transforme tout point M distinct de C en un point M' tel que

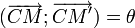
CM = CM' et (\overrightarrow{CM};\overrightarrow{CM'} )= \theta

Les rotations les plus classiques sont

  • les quarts de tour directs - rotations d'angle droit dans le sens trigonométrique (i.e. inverse des aiguilles d'une montre);
  • les quarts de tours indirects - rotations d'angle droit dans le sens des aiguilles d'une montre
  • les rotations d'angle plat qui correspondent aux symétries centrales et aux homothéties de rapport -1
  • Une rotation d'angle nulle correspond à l'identité.

Construction de l'image d'un point par une rotation: prévoir figure

  • Tracer le cercle de centre C et de rayon [CM].
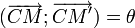  • Placer sur ce cercle le point M' , qui est l'image de M par cette rotation tel que (\overrightarrow{CM};\overrightarrow{CM'}) = \theta.

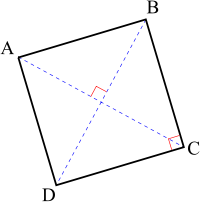
Une rotation peut aussi être déterminée par un centre et l'image d'un point : Si C est un point et A et A' deux points distincts de C tels que CA = CA', il existe une unique rotation de centre C et qui transforme A en A'. L'angle 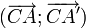(\overrightarrow{CA};\overrightarrow{CA'}) est alors l'angle de la rotation.

Propriétés

Propriété 1 : L'image d'un segment [AB] est un segment [ A'B' ] tel que AB = A'B' .

Propriété 2 : L'image d'un cercle C de centre O et de rayon r est un cercle C' de centre O' , l'image de O, et de même rayon r.

Propriété du vecteur image

Propriété 3 dite "de conservation" : La rotation conserve :

  • les longueurs ;
  • les angles (l'image d'un angle est un angle de même mesure) ;
  • les parallèles (les images de deux droites parallèles sont parallèles) ;
  • les aires (l'image d'une figure est une figure de même aire).

La rotation conserve donc les distances, c’est-à-dire que M'N' = MN. C'est donc une isométrie. Elle conserve donc les alignements, les angles et les concours. Elle conserve aussi l'orientation : si ABC est un triangle direct alors A'B'C' est aussi un triangle direct.

Fait important, on retrouve aussi l'angle de la rotation entre un vecteur et son image.


Démonstrations

Les triangle CMN et C'M'N' sont isométriques de même orientation car : CM = CM'

CN = CN'
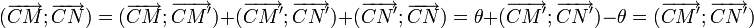
( \overrightarrow{CM};\overrightarrow{CN}) = (\overrightarrow{CM};\overrightarrow{CM'}) + ( \overrightarrow{CM'};\overrightarrow{CN'}) + ( \overrightarrow{CN'};\overrightarrow{CN})= \theta + ( \overrightarrow{CM'};\overrightarrow{CN'}) - \theta = ( \overrightarrow{CM'};\overrightarrow{CN'})

Donc, en particulier

MN = M'N'
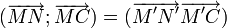
( \overrightarrow{MN};\overrightarrow{MC}) = (\overrightarrow{M'N'}\overrightarrow{M'C})

Une relation de Chasles sur les vecteurs permet alors d'écrire :

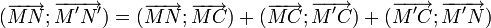
( (\overrightarrow{MN};\overrightarrow{M'N'}) = ( \overrightarrow{MN};\overrightarrow{MC}) + ( \overrightarrow{MC};\overrightarrow{M'C}) + (\overrightarrow{M'C};\overrightarrow{M'N})

les deux angles extrêmes s'annulent et celui du milieu vaut θ donc

( \overrightarrow{MN};\overrightarrow{M'N'}) = \theta

Autre caractérisation

Une rotation peut donc être caractérisée par l'image de deux points : Soient A et B deux points distincts et A' B' deux points tels que AB = A'B' avec 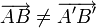\overrightarrow{AB} \ne \overrightarrow{A'B'}, il existe une unique rotation r qui transforme A en A' et B en B'. Cette rotation pour angle 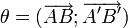\theta = (\overrightarrow{AB}; \overrightarrow{A'B'}), et pour centre l'intersection des médiatrices de [AA'] et [BB'] (si elles se coupent) ou bien le point d'intersection de (AB) et de la médiatrice de [AA'] (si les médiatrices ne sont pas sécantes). Il n'est pas nécessaire de connaitre le centre de la rotation pour construire l'image M' du point M (distinct de A) car celui-ci vérifie les deux conditions suivantes:

AM = A'M'
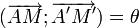
( \overrightarrow{AM};\overrightarrow{A'M'}) = \theta

qui le définissent de manière univoque

Cas des médiatrices sécantes
Cas des médiatrices confondues

Rem: Si l'une des médiatrices n'existe pas, ce qui se produit quand A et A' ou B et B' sont confondus, le centre est alors immédiat : c'est, selon les cas, A ou B.

Invariance par rotation

Certaines figures sont invariantes par rotation. C'est le cas par exemple du carré de centre O, invariant par rotation de centre O et d'angle droit ou plat, ou du triangle équilatéral de centre O invariant par rotation d'angle 120°. On dit alors que ces figures possèdent une symétrie d'ordre 4 (pour le carré) ou d'ordre 3 (pour le triangle). L'ordre de la rotation correspond au nombre de rotations nécessaires pour revenir au point de départ.

Carré et centre de rotation
Triangle équilatéral et centre de rotation

Un polygone régulier à n côtés possède une symétrie d'ordre n. Il existe des figures possédant une symétrie d'ordre n qui ne possèdent pas pour autant un axe ou un centre de symétrie. C'est le cas par exemple du Triskell qui possède une symétrie d'ordre trois (Rq: à cause de l'alternance noir/blanc, le Taijitu, symbole du Yin Yang ne possède pas la symétrie d'ordre deux qu'on pourrait lui prêter au premier abord).

Symbole Yin-Yang
Triskell

Composition et décomposition

Composée de deux réflexions

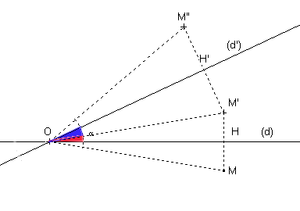
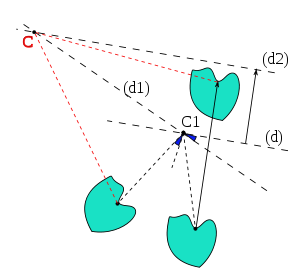
La composée de deux réflexions (ou symétries) s (d) et s (d') d'axes sécants en O est une rotation de centre O . Plus précisément, si

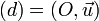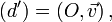
(d)= (O, \vec u) et (d') = (O, \vec v)\,,

alors

s_{(d')} \circ s_{(d)} = r

où r est une rotation de centre O et d'angle θ

\theta=2(\vec u, \vec v)\,.

Réciproquement, toute rotation de centre C se décompose en deux réflexions (symétries) d'axes sécants en C dont l'un peut être choisi arbitrairement pourvu que l'autre permette, en multipliant par deux l'angle formé par les vecteurs directeurs, de retrouver l'angle de la rotation.

La composée de deux rotations de même centre C et d'angles θ et θ' est une rotation de centre C et d'angle θ + θ'. Ces deux rotations commutent, c’est-à-dire que
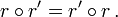
r \circ r' = r' \circ r\,.
L'ensemble des rotations de centre C, muni de la loi de composition est donc un groupe commutatif isomorphe à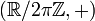 (\mathbb R/2\pi\mathbb Z, +)

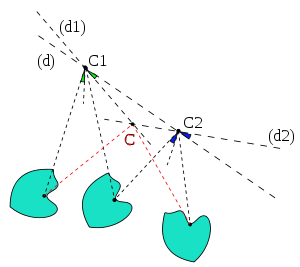
La composée de deux rotations de centres différents et d'angles θ et θ' est

  • une rotation d'angle θ + θ' si θ + θ' ≠ 2kπ
  • une translation sinon

La recherche du nouveau centre et la démonstration de cette propriété s'obtient en décomposant chaque rotation en deux réflexions ayant un axe en commun. Cette composée est rarement commutative.

De plus, la composée d'une rotation et d'une translation reste une rotation de même angle dont le centre a changé.

Composée de deux rotations
Composée d'une rotation et d'une translation

L'ensemble formé de toutes les rotations planes et de toutes les translations, muni de la loi de composition interne forme un groupe non commutatif appelé le groupe des isométries directes.

Expression complexe

La rotation de centre C et d'angle θ a pour expression complexe

z' = e^{i\theta}(z - z_c) + z_c\,

c’est-à-dire que, si zc est l'affixe de C, le point M d'affixe z a pour image le point M' d'affixe z' vérifiant l'égalité précédente.

Réciproquement, toute transformation dont l'expression complexe est

z' = az + b, où a et b sont des complexes, vérifiant |a| = 1 et a ≠ 1

est une rotation dont le centre C a pour affixe 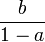\dfrac{b}{1-a} et dont l'angle est l'argument de a

Cette écriture complexe permet de retrouver aisément toutes les propriétés précédentes.

Formules de changement d'axes de coordonnées

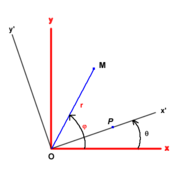
Il est courant en physique de devoir opérer une rotation des axes de coordonnées. Les formules qui suivent permettent d'exprimer les coordonnées d'un point M dans l'un des repères en fonction des coordonnées dans l'autre repère. Prenons un repère cartésien xOy dans lequel les coordonnées (x, y ) d'un point M s'expriment en fonction des coordonnées polaires (r, φ) par les formules élémentaires

\begin{cases}x= r \cos\,\phi\\ y = r \sin\,\phi \,. \end{cases}
Changement de repère par rotation d'angle θ

Dans le nouveau repère x'Oy' déduit du précédent par une rotation d'angle θ (voir la figure) les nouvelles coordonnées polaires sont r et (φ - θ) et les coordonnées cartésiennes deviennent

\begin{cases} x'=r\cos\,(\phi- \theta)\\y'=r\sin\,(\phi-\theta) \,. \end{cases}

En développant les fonctions trigonométriques et en tenant compte des expressions de x et y on arrive aux formules suivantes permettant de passer d'un repère à l'autre.

\begin{cases}x'=x\cos\,\theta+y\sin\,\theta\\y'=-x\sin\,\theta + y\cos\,\theta\end{cases}

et, en sens inverse,

\begin{cases}x=x'\cos\,\theta-y'\sin\,\theta\\y=x'\sin\,\theta + y'\cos\,\theta\end{cases}

Un truc : s'il peut s'avérer difficile de mémoriser le signe à mettre devant sinθ (« + » dans une ligne et « - » dans l'autre) l'astuce consiste à considérer un point particulier (tel que P sur la figure) avec y = 0 ou y ’ = 0 selon les besoins et de vérifier alors sur la figure le signe de la coordonnée voulue.

Voir aussi

Sur les autres projets Wikimedia :

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Rotation plane ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Rotation (mathématiques élémentaires) de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Mathématiques élémentaires — Les mathématiques élémentaires[1] regroupent des notions et techniques mathématiques abordées dans l enseignement scolaire primaire et secondaire. Elles se démarquent ainsi des mathématiques de l enseignement supérieur et notamment, en France,… …   Wikipédia en Français

  • Probabilités (mathématiques élémentaires) — Pour les articles homonymes, voir Interconnexions entre la théorie des probabilités et les statistiques. Les probabilités sont nées du désir de prévoir l imprévisible ou de quantifier l incertain. Mais il faut avant tout préciser ce qu elles ne… …   Wikipédia en Français

  • Fonction (mathématiques élémentaires) — Pour les articles homonymes, voir Fonction. En mathématiques élémentaires, la plupart des fonctions rencontrées sont des fonctions numériques, mais la notion de fonction ne se limite pas à celle ci. L article qui suit présente quelques règles à… …   Wikipédia en Français

  • Statistiques (mathématiques élémentaires) — Une enquête statistique consiste à observer une certaine population (élèves d’une classe, personnes âgées de 20 à 60 ans dans une région donnée, familles dans une région donnée, exploitations agricoles, appartements, travailleurs…) et à… …   Wikipédia en Français

  • Limite (mathématiques élémentaires) — Pour les articles homonymes, voir Limite. La notion de limite est très intuitive malgré sa formulation abstraite. Pour les mathématiques élémentaires, il convient de distinguer une limite en un point réel fini (pour une fonction numérique) et une …   Wikipédia en Français

  • Logique (mathématiques élémentaires) — La logique est le lieu où le langage puis les axiomes (logiques ou propres à certaines théories) des mathématiques sont définis ce qui est à la base des démonstrations en mathématique. Bien qu elle apparaisse de manière cachée dans toute l… …   Wikipédia en Français

  • Suite (mathématiques élémentaires) — Intuitivement une suite réelle est une règle qui associe à chaque entier naturel n un certain nombre réel ; on dit alors que ce nombre réel est indexé par l’entier. En fait une suite est un moyen d’indexer des nombres réels par des entiers… …   Wikipédia en Français

  • Distributivité (mathématiques élémentaires) — La distributivité est une propriété de la multiplication qui permet d effectuer de deux manières différentes le produit d un nombre par une somme : Ici on a distribué a à chaque terme de la somme Ici on a distribué c à chaque terme de la… …   Wikipédia en Français

  • Démonstration (mathématiques élémentaires) — Démontrer une propriété c est utiliser des théorèmes, des définitions ou des axiomes que l on sait être vrais et quelques règles de logique élémentaire. Elle expose une justification d’une propriété nouvelle algébrique, géométrique, numérique…… …   Wikipédia en Français

  • Série (mathématiques élémentaires) — Pour les articles homonymes, voir Série. Les séries sont une catégorie de suite. Une série de terme général un est, basiquement, la somme des n premiers termes de la suite . C est pour cette raison que l on appelle la suite , la suite des sommes… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”