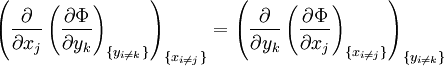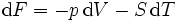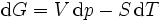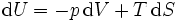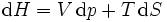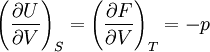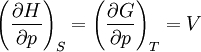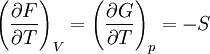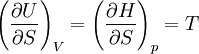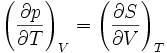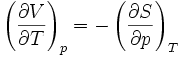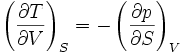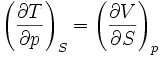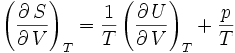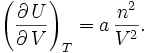Relation de Maxwell

Relations de Maxwell

Ne doit pas être confondu avec Équations de Maxwell.

En thermodynamique, on appelle relations de Maxwell l'ensemble des équations aux dérivées partielles obtenues grâce aux définitions des potentiels thermodynamiques et à l'égalité de Schwarz. Pour un système entièrement décrit par les variables pression, température, entropie et volume, on retient généralement un ensemble de quatre relations relatives à l'énergie interne, à l'enthalpie, à l'énergie libre et à l'enthalpie libre. Néanmoins les relations de Maxwell sont généralisables à tous les systèmes thermodynamiques notamment chimiques, électriques et électrochimiques.

Sommaire

1 Définition générale
2 Systèmes p, T, V, S
- 2.1 Une application : première loi de Joule
3 Notations utilisées dans cet article

Définition générale

Soit un potentiel thermodynamique $Φ$ dont les variables naturelles sont les variables conjuguées $x i$ et $y i$ . L'application du théorème de Schwartz permet d'obtenir :

$\left(\frac{\partial}{\partial x_j} \left(\frac{\partial \Phi}{\partial y_k} \right)_{\{y_{i\ne k}\}} \right)_{\{x_{i\ne j}\}} = \left(\frac{\partial}{\partial y_k} \left(\frac{\partial \Phi}{\partial x_j} \right)_{\{x_{i\ne j}\}} \right)_{\{y_{i\ne k}\}}$

Systèmes p, T, V, S

Pour les systèmes définis par les quatre variables pression, température, volume et entropie, on définit par l'intermédiaire de différentielles totales exactes quatre potentiels thermodynamiques :

$\mathrm{d}F = -p\,\mathrm{d}V - S\,\mathrm{d}T ~$

$\mathrm{d}G = V\,\mathrm{d}p - S\,\mathrm{d}T ~$

$\mathrm{d}U = -p\,\mathrm{d}V + T\,\mathrm{d}S ~$

$\mathrm{d}H = V\,\mathrm{d}p + T\,\mathrm{d}S ~$

Les relations de Maxwell qu'on en tire permettent notamment de définir thermodynamiquement la température, la pression, l'entropie et le volume.

$\left(\frac{\partial U}{\partial V}\right)_S =\left(\frac{\partial F}{\partial V}\right)_T = - p ~$

$\left(\frac{\partial H}{\partial p}\right)_S =\left(\frac{\partial G}{\partial p}\right)_T = V ~$

$\left(\frac{\partial F}{\partial T}\right)_V =\left(\frac{\partial G}{\partial T}\right)_p = - S ~$

$\left(\frac{\partial U}{\partial S}\right)_V =\left(\frac{\partial H}{\partial S}\right)_p = T ~$

on trouve aussi :

$\left(\frac{\partial p}{\partial T}\right)_V = \left(\frac{\partial S}{\partial V}\right)_T ~$

$\left(\frac{\partial V}{\partial T}\right)_p = -\left(\frac{\partial S}{\partial p}\right)_T ~$

$\left(\frac{\partial T}{\partial V}\right)_S = -\left(\frac{\partial p}{\partial S}\right)_V ~$

$\left(\frac{\partial T}{\partial p}\right)_S = \left(\frac{\partial V}{\partial S}\right)_p ~$

Une application : première loi de Joule

Pour un gaz parfait, on a donc d'après ce qui précède

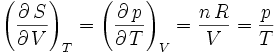$\left(\frac{\partial\,S}{\partial\,V}\right)_T=\left(\frac{\partial\,p}{\partial\,T}\right)_V=\frac{n\,R}{V}=\frac{p}{T}$ .

D'autre part,

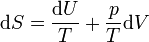$\mathrm{d}S=\frac{\mathrm{d}U}{T} + \frac{p}{T} \mathrm{d}V$ .

Soit:

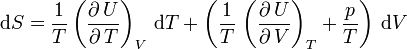$\mathrm{d}S= \frac{1}{T}\left(\frac{\partial\,U}{\partial\,T}\right)_{V}\,\mathrm{d}T+\left(\frac{1}{T}\,\left(\frac{\partial\,U}{\partial\,V}\right)_{T}+\frac{p}{T}\right)\,\mathrm{d}V$ .

Ainsi,

$\left(\frac{\partial\,S}{\partial\,V}\right)_{T}=\frac{1}{T}\left(\frac{\partial\,U}{\partial\,V}\right)_{T}+\frac{p}{T}$

d'où, d'après ce qui précède,

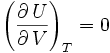$\left(\frac{\partial\,U}{\partial\,V}\right)_{T}=0$ :

l'énergie interne d'un gaz parfait ne dépend que de sa température.

En effectuant ces calculs pour un gaz de van der Waals, c'est-à-dire un gaz dont l'équation d'état est

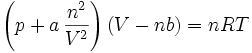$\left(p+a\,\frac{n^{2}}{V^{2}}\right)\left(V-nb\right)=nRT$ ,

on trouve

$\left(\frac{\partial\,U}{\partial\,V}\right)_{T}=a\,\frac{n^{2}}{V^{2}}.$

Cette méthode ne permet pas d'expliciter la dépendance de U en T : en effet, on sait par ailleurs qu'elle fait intervenir le coefficient de Laplace $γ$ qui n'apparaît ni dans les identités thermodynamiques ni dans l'équation d'état.

Notations utilisées dans cet article

$V$ : Volume
$p$ : Pression
$T$ : Température
$U$ : Énergie interne
$H$ : Enthalpie
$F$ : Énergie libre
$G$ : Enthalpie libre
$S$ : Entropie
$R$ : Constante des gaz parfaits
$a$ et $b$ : paramètres de l'équation d'état de van der Waals

Portail de la physique

Ce document provient de « Relations de Maxwell ».

Catégorie : Thermodynamique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Relation de Maxwell de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Relation de gibbs-helmholtz — La relation de Gibbs Helmholtz (nom donné en l honneur des physiciens Gibbs et Helmholtz) est donnée par : Avec: H l enthalpie G l enthalpie libre T la température (absolue) On trouve aussi d autres formulations équivalentes de cette… … Wikipédia en Français
Relation de Gibbs-Helmholtz — La relation de Gibbs Helmholtz (nom donné en l honneur des physiciens Gibbs et Helmholtz) est donnée par : Avec: H l enthalpie G l enthalpie libre T la température (absolue) On trouve aussi d autres formulations équivalentes de cette… … Wikipédia en Français
Maxwell House — Type Subsidiary Industry Beverage Founded 1892 Headquarters H … Wikipedia
Maxwell — may refer to: Contents 1 People 1.1 Surname 1.2 Given name 1.3 Fictional people 2 Places … Wikipedia
Maxwell Montes — Radar image of Maxwell Montes Feature type Mountain range Coordinates … Wikipedia
RELATION — Le concept de relation apparaît comme l’un des concepts fondamentaux du discours rationnel. Il semble lié à la pratique de l’analyse, qui constitue elle même l’un des aspects essentiels de la démarche discursive. L’analyse décompose les unités… … Encyclopédie Universelle
Maxwell-Beziehung — [ mækswəl ; nach J. C. Maxwell], Maxwell Relation, die Verknüpfung der (absoluten) Brechzahl n = c0 / c mit der relativen Dielektrizitätskonstanten εr und der relativen Permeabilität μ … Universal-Lexikon
Maxwell relations — Thermodynamics … Wikipedia
Maxwell's equations — For thermodynamic relations, see Maxwell relations. Electromagnetism … Wikipedia
Maxwell-Relation — Die nach dem Physiker James Clerk Maxwell benannten Maxwell Beziehungen oder Maxwell Relationen stellen wichtige Zusammenhänge zwischen verschiedenen Größen her. Thermodynamik Die maxwellschen Beziehungen der Thermodynamik erlauben es, Änderungen … Deutsch Wikipedia

Dictionnaires et Encyclopédies sur 'Academic'

Relation de Maxwell

Relations de Maxwell

Sommaire

Définition générale

Systèmes p, T, V, S

Une application : première loi de Joule

Notations utilisées dans cet article

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Relation de Maxwell

Relations de Maxwell

Sommaire

Définition générale

Systèmes p, T, V, S

Une application : première loi de Joule

Notations utilisées dans cet article

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link