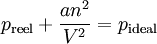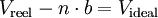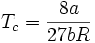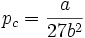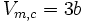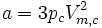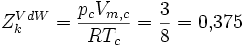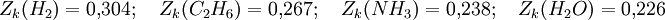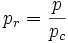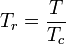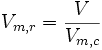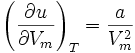Equation d'etat de van der Waals

Equation d'etat de van der Waals

Équation d'état de van der Waals

L'équation d'état de Van der Waals, d'après Johannes Diderik van der Waals (1873) est une équation d'état approchée pour les gaz réels. Elle est l'équation d'état d'un gaz de Van der Waals.

Sous sa forme intensive, elle peut s'écrire :

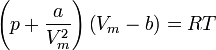
\left( p + \frac{a}{V^2_m}\right)\left(V_m - b \right) = RT

ou

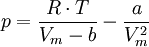
\, \, p = \frac{R \cdot T}{V_m - b}-\frac{a}{V^2_m}

et sous sa forme extensive :

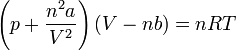
\left( p + \frac{n^2 a}{V^2}\right)\left(V-nb \right) = nRT

avec :

Une autre équation d'état approchée pour les gaz réels est le développement du viriel. L'équation de Van der Waals et la loi des gaz parfaits sont des approximations du développement du viriel.

Gaz a en (kPa·dm6)/mol2 b en dm3/mol
Hélium (He) 3,45 0,0237
Néon (Ne) 21,3 0,0171
Argon (Ar) 136,3 0,0322
Hydrogène (H2) 24,7 0,0266
Azote (N2) 140,8 0,0391
Oxygène (O2) 137,8 0,0318
Air (80% N2, 20% O2) 135,8 0,0364
Dioxyde de carbone (CO2) 363,7 0,0427
Eau (H2O) 557,29 0,031
Chlore (Cl2) 657,4 0,0562
Ammoniac (NH3) 422,4 0,0371
Méthane (CH4) 225 0,0428
Données expérimentales sujettes à d'importantes variations.
Gaz a en (bar·dm6)/mol2 b en dm3/mol
Benzène (C6H6) 52,74 0,3043
Décane (C10H22) 37,88 0,2374
Octane (C8H18)) 18,82 0,1193
Données valables pour la phase gazeuse uniquement.

Sommaire

Origine et établissement

En pratique, les gaz ne se comportent pas exactement comme le décrit la loi des gaz parfaits, car ils sont composés de molécules ayant un certain volume. La loi des gaz parfaits ignore le fait que les molécules possèdent un volume propre; le volume d'un gaz réel est donc supérieur au volume d'un gaz idéal (Vidéal < Vréel). En outre, des interactions autres que les simples chocs élastiques du modèle des gaz parfaits existent entre les molécules. Les forces attractives entre les molécules font que la pression d'un gaz réel est inférieure à la pression d'un gaz idéal, en particulier pour les hautes pressions (préel < pidéal).

Les gaz idéaux ne peuvent, de plus, devenir liquides ou solides, indépendamment de la pression ou de la température. Il est donc nécessaire d'ajuster la loi des gaz parfaits pour décrire le comportement des gaz réels. L'équation de Van der Waals s'obtient, contrairement à l'équation des gaz parfaits, à partir d'un modèle de gaz composé de sphères dures soumises à des interactions dipôlaires attractives appelées forces de Van der Waals, ce qui conduit aux adaptations suivantes :

p_{\rm reel} + \frac{a n^2}{V^2} = p_{\rm ideal} \!
V_{\rm reel} - n \cdot b = V_{\rm ideal} \!

En utilisant ces grandeurs dans l'équation des gaz parfaits, on obtient l'équation de Van der Waals.

Propriétés

Les paramètres a et b sont déterminés expérimentalement, ne représentent pas de constantes particulières et dépendent eux-mêmes d'autres grandeurs. Le covolume b représente le volume propre des atomes d'une mole de gaz et s'interprète comme un volume exclu (il est impossible de rendre le volume du gaz inférieur à b). Le terme an2/V2 permet de prendre en compte l'attirance mutuelle des atomes du gaz, on l'appelle également pression de liaison. L'équation de Van der Waals n'est plus valable pour les fortes pressions, car le volume propre supposé fixe n'autorise pas une compression à un volume molaire inférieur à b, ce qui ne correspond pas au comportement des gaz réels.

L'équation de Van der Waals a cet avantage de décrire la phase liquide ainsi que la phase gazeuse, mais elle ne décrit pas le comportement de gaz réels avec précision : son intérêt est plutôt théorique. Cette équation d'état possède en effet la propriété de décrire une transition de phase du premier ordre entre un état liquide et un état gazeux ainsi que son point critique au delà duquel le passage entre le liquide et le gaz se fait continûment. Dans le point critique du gaz de Van der Waals, les exposants critiques obtenus sont α = 0, β = 1 / 2 et γ = 1, comme dans toute approximation de champ moyen. Les exposants critiques réels sont ceux du modèle d'Ising en dimension 3, la différence entre la densité du gaz et la densité du liquide jouant le role d'un paramètre d'ordre scalaire.

Des équations d'états plus précises existent, comme l'équation de Redlich-Kwong, ou bien l'équation de Redlich-Kwong-Soave, plus évoluées même si également semi-empiriques. Il existe également des équations d'état empiriques, comme par exemple l'équation de Benedict-Webb-Rubin.

Isothermes du diagramme p-V

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Estimations des grandeurs critiques

Le point critique joue un rôle important pour les gaz réels. On peut définir les grandeurs et relations suivantes à partir de l'équation de Van der Waals :

T_c = \frac{8a}{27bR}
p_c = \frac{a}{27b^2}
  • Volume molaire critique :
V_{m, c} = 3b \!
  • Combinaison du volume molaire critique et de la pression critique :
a = 3 p_c V_{m, c}^2

Lorsque l'on introduit ces grandeurs dans l'équation d'état, on fait apparaître une nouvelle constante :

Z_k^{VdW} = \frac{p_c V_{m, c}}{R T_c} = \frac{3}{8} = 0{,}375

Zk est appelé facteur de compressibilité critique. Dans l'équation de Van der Waals, cette grandeur est constante, mais cela ne correspond pas au comportement de gaz réels. En règle générale, le facteur de compressibilité critique vaut de 0,25 à 0,3. La déviation observée montre le caractère approchée de l'équation de Van der Waals.

On a par exemple :

Z_k(H_2) = 0{,}304; \quad Z_k(C_2H_6) = 0{,}267; \quad Z_k(NH_3) = 0{,}238; \quad Z_k(H_2O) = 0{,}226

Forme réduite

Les grandeurs réduites utilisent le point critique de chaque gaz comme point de comparaison, en divisant les grandeurs d'état par leur expression critique. Elles sont adimensionnelles et définies comme suit :

  • Pression réduite :
p_r = \frac{p}{p_c}
  • Température réduite :
T_r = \frac{T}{T_c}
  • Volume molaire réduit :
V_{m, r} = \frac{V}{V_{m, c}}

Deux gaz de grandeurs réduites semblables ont des propriétés proches.

On peut également formuler l'équation de Van der Waals réduite :

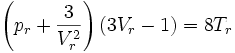
\left( p_r + \frac{3}{V_r^2} \right) (3 V_r - 1) = 8 T_r

Énergie interne

L'énergie interne d'un gaz de Van der Waals dépend du volume molaire :

\left( {\partial u \over \partial V_m} \right)_{T} = \frac{a}{V_m^2}

Elle n'est pas uniquement composé de l'énergie cinétique des molécules, mais également de l'énergie potentielle des forces de cohésion, décrites par le paramètre a.

Notes et références

  • (de) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en allemand intitulé « Van-der-Waals-Gleichung ».
  • Lev Landau et Evguéni Lifchitz, Physique théorique, éd. MIR, Moscou [détail des éditions]
  • Y. Rocard Thermodynamique (Gauthier-Villars)
  • G. Bruhat Thermodynamique (Masson)
  • Portail de la physique Portail de la physique
Ce document provient de « %C3%89quation d%27%C3%A9tat de van der Waals ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Equation d'etat de van der Waals de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Équation d'état de Van der Waals — L équation d état de Van der Waals, d après Johannes Diderik van der Waals (1873) est une équation d état approchée pour les gaz réels. Elle est l équation d état d un gaz de Van der Waals. Sous sa forme intensive, elle peut s écrire : ou et …   Wikipédia en Français

  • Équation d'état de van der Waals — L équation d état de van der Waals, d après Johannes Diderik van der Waals (1873) est une équation d état approchée pour les gaz réels. Elle est l équation d état d un gaz de van der Waals. Sommaire 1 Origine et établissement 2 Propriétés 3… …   Wikipédia en Français

  • Equation de Van der Waals — Équation d état de van der Waals L équation d état de Van der Waals, d après Johannes Diderik van der Waals (1873) est une équation d état approchée pour les gaz réels. Elle est l équation d état d un gaz de Van der Waals. Sous sa forme intensive …   Wikipédia en Français

  • Équation de Van der Waals — Équation d état de van der Waals L équation d état de Van der Waals, d après Johannes Diderik van der Waals (1873) est une équation d état approchée pour les gaz réels. Elle est l équation d état d un gaz de Van der Waals. Sous sa forme intensive …   Wikipédia en Français

  • Équation de van der waals — Équation d état de van der Waals L équation d état de Van der Waals, d après Johannes Diderik van der Waals (1873) est une équation d état approchée pour les gaz réels. Elle est l équation d état d un gaz de Van der Waals. Sous sa forme intensive …   Wikipédia en Français

  • Van Der Waals — Johannes Diderik van der Waals Johannes Diderik van der Waals Johannes Diderik van der Waals, fils de Jacobus van der Waals et d’Elisabeth van den Burg, est un physicien né à Leyde le 23 novembre 1837 et mort le 8 mars  …   Wikipédia en Français

  • Van der Waals — Johannes Diderik van der Waals Johannes Diderik van der Waals Johannes Diderik van der Waals, fils de Jacobus van der Waals et d’Elisabeth van den Burg, est un physicien né à Leyde le 23 novembre 1837 et mort le 8 mars  …   Wikipédia en Français

  • Liste des constantes de van der Waals — Le tableau suivant donne, à partir de l’équation d état de van der Waals, la liste des constantes de van der Waals pour un certain nombre de gaz communs et de liquides volatils. Unités : 1 J·m3·mol 2 = 1 m6·Pa·mol 2 =… …   Wikipédia en Français

  • Johannes Diderik van der Waals — Naissance 23 novembre 1837 Leyde (Pays Bas) Décès 8  …   Wikipédia en Français

  • Rayon de van der Waals — Rayons de van der Waals de certains éléments Élément Rayon (Å) Hydrogène 1,20 Carbone 1,70 Azote 1,55 Oxygène 1,52 Fluor 1,47 Phosphore …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”