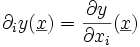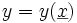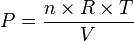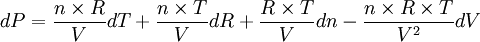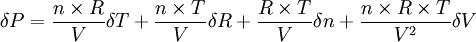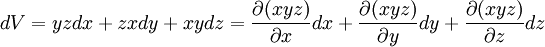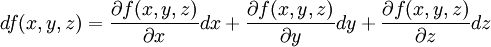Propagation des erreurs

Une mesure est toujours entachée d'erreur. Lorsqu'une valeur mesurée est utilisée dans une formule, il faut savoir estimer l'erreur induite sur le résultat de la formule. On parle de propagation d'erreur.

Sommaire

1 Approches pragmatiques
- 1.1 Report des extrêmes dans le calcul
- 1.2 Estimation à partir de la dérivée
2 Approche mathématique
- 2.1 Notations
- 2.2 Formules
3 Applications
- 3.1 Mesure d'une résistance
- 3.2 Utilisation des différentielles totales exactes
4 Liens externes

Approches pragmatiques

Report des extrêmes dans le calcul

La première solution consiste à effectuer les calculs avec les extrêmes de l'intervalle d'erreur. Si la mesure a pour valeur

a ± Δa

alors la « valeur réelle » est supposée être dans l'intervalle [a-Δa;a+Δa]. On calcule donc ici

y₁ = ƒ(a-Δa)

y₂ = ƒ(a+Δa)

et, selon l'ordre de y₁ et de y₂, on prend [y₁;y₂] ou [y₂;y₁] comme intervalle d'erreur.

Cette méthode n'est valable que si la loi est monotone (c'est-à-dire croissante ou décroissante) sur l'intervalle [a-Δa;a+Δa].

Estimation à partir de la dérivée

Une manière simple, utilisée fréquemment en physique, consiste à utiliser un développement limité du premier ordre, c'est-à-dire à remplacer la loi ƒ par sa « tangente » pour estimer l'erreur. On estime ainsi l'erreur avec une loi uniforme (linéaire) et simple.

On a :

ƒ(x) = ƒ(a) + ƒ '(a)·(x-a) + o(x)

où o(x) est une fonction qui « tend vite » vers 0. Si l'on remplace x par a + Δa, on a alors

ƒ(a + Δa) = ƒ(a) + ƒ '(a)·Δa + o(a + Δa)

On peut donc estimer

Δy ≈ ƒ '(a) · Δa

Cette erreur est sous-estimée si l'on a une loi convexe.

Approche mathématique

Notations

x une variable aléatoire,
E(x) ou <x> l'espérance mathématique de x,
V(x) la variance de x.
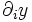$\partial_i y$ est la dérivée partielle de la fonction y par rapport à la i ^e variable.

par exemple, si x est un vecteur (x₁, x₂,…, x_n), alors

$\partial_i y(\underline{x}) = \frac{\partial y}{\partial x_i}(\underline{x})$

Formules

Une fonction de variables aléatoires

$y = y (\underline{x})$

est elle-même une variable aléatoire. Si les erreurs sont petites, la variance du développement limité de y au premier ordre autour des valeurs moyennes μ des x est une bonne estimation de la variance de y :

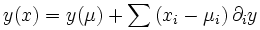
$y(x) = y(\mu) + \sum \left(x_i - \mu_i \right) \partial_i y$

On néglige les termes d'ordre supérieur dans l'expansion, il vient :

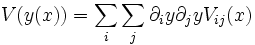
$V(y(x)) = \sum_i\sum_j \partial_i y \partial_j y V_{ij}(x)$

Si les x sont indépendantes

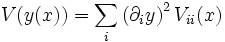
$V(y(x)) = \sum_i \left( \partial_i y \right)^2 V_{ii}(x)$

Applications

Mesure d'une résistance

Une application pratique est la mesure expérimentale d'une résistance R à partir de la chute de tension U entre ses bornes et du courant I. La résistance est décrite par la loi d'Ohm.

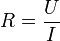
$R = \frac{U}{I}$

Nous avons

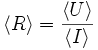
$\langle R \rangle = \frac{\langle U \rangle}{\langle I \rangle}$

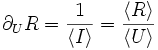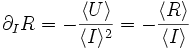
$\partial_U R = \frac{1}{\langle I \rangle} = \frac{\langle R \rangle}{\langle U \rangle}$ et $\partial_I R = - \frac{\langle U \rangle}{\langle I \rangle^2} = - \frac{\langle R \rangle}{\langle I \rangle}$

Il vient

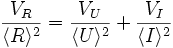
$\frac{V_R}{\langle R \rangle^2} = \frac{V_U}{\langle U \rangle^2} + \frac{V_I}{\langle I \rangle^2}$

Dans ce cas simple, l'incertitude relative sur R correspond à la moyenne géométrique des incertitudes relatives sur U et I :

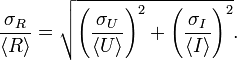
$\frac{\sigma_R}{\langle R \rangle} = \sqrt{\left(\frac{\sigma_U}{\langle U \rangle}\right)^2 + \left(\frac{\sigma_I}{\langle I \rangle}\right)^2}.$

Cette formule est différente de la formule basée sur la différentielle totale exposée ci-dessous :

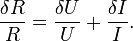
$\frac{\delta R}{R} = \frac{\delta U}{U} + \frac{\delta I}{I}.$

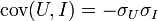La raison en est que la deuxième formule considère ce qui peut arriver dans le « pire » des cas : celui où U s'écarte de δU de sa valeur moyenne et où I s'écarte de –δI. Pour retrouver cette formule par application de la loi de propagation des erreurs, il faut supposer que les variables U et I sont parfaitement corrélées (plus exactement, le coefficient de corrélation est égal à -1 : $\operatorname{cov}(U,I)=-\sigma_U \sigma_I$ )

Utilisation des différentielles totales exactes

Une loi physique s'exprime par une relation algébrique entre un cerain nombre de grandeurs mesurables :

P : pression du gaz
V : volume occupé par le gaz
n : quantité de gaz en moles (1 mole = 6,022·10²³ molécules)
R : constante des gaz parfaits = 8,314 J·K^-1·mol^-1
T : température absolue du gaz, en kelvin

La pression en fonction de n, R, T et V s'exprime par

$P =\frac{n \times R \times T}{V}$

écrivons sa différentielle :

$dP =\frac{n \times R}{V} dT + \frac{n \times T}{V} dR + \frac{ R \times T}{V}dn - \frac{n \times R \times T}{V^2}dV$

Si l'on « remplace » des variations élémentaires de variables dx par les erreurs sur les variables δx, on obtient :

$\delta P =\frac{n \times R}{V}\delta T + \frac{n \times T}{V}\delta R +\frac{ R \times T}{V}\delta n + \frac{n \times R \times T}{V^2}\delta V$

qui donne l'erreur absolue sur P déduite du calcul de P à partir de la connaissance des erreurs sur T, R, n et V.

Autres exemples simples :

le calcul de la surface d'un rectangle.

S = L l

S + d S = (L + d L)(l + d l) = L l + L d l + l d L + d l d L

peut s'écrire

d S = ((L + d L)(l + d l) - L l) = L d l + l d L + d L d l

que l'on approxime par

d S = L d l + l d L

le calcul d'un volume V = x·y·z

V (x + d x, y + d y, z + d z) = (x + d x)(y + d y)(z + d z) = x y z + d x y z + x d y z + x y d z + x d y d z + y d x d z + z d x d y + d x d y d z

peut s'écrire

d V = y z d x + z x d y + x y d z + d x d y d z

que l'on approxime par

d V = y z d x + z x d y + x y d z

noter que

$dV = yz dx +zx dy + xy dz = \frac{\partial (xyz) }{\partial x}dx+\frac{\partial (xyz) }{\partial y}dy+\frac{\partial (xyz) }{\partial z}dz$

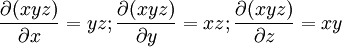
rappel: $\frac{\partial (xyz) }{\partial x}= yz ; \frac{\partial (xyz) }{\partial y}=xz ; \frac{\partial (xyz) }{\partial z}=xy$

et plus généralement pour le calcul de la variation d'une fonction ƒ(x,y,z).

si 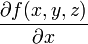$\frac{\partial f(x,y,z) }{\partial x}$ est la dérivée partielle par rapport à x

$d f(x,y,z) = \frac{\partial f(x,y,z) }{\partial x}dx+\frac{\partial f(x,y,z) }{\partial y}dy+\frac{\partial f(x,y,z)}{\partial z}dz$

Liens externes

Portail des mathématiques

Ce document provient de « Propagation des erreurs ».

Catégories : Métrologie | Analyse réelle

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Propagation des erreurs de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Propagation des incertitudes — Une mesure est toujours entachée d erreurs dont on estime l intensité par l intermédiaire des incertitudes. Lorsqu une mesure est utilisée pour obtenir la valeur d une autre grandeur par l intermédiaire une formule, outre le calcul de la valeur… … Wikipédia en Français
Propagation des ondes radio — Les ondes radioélectriques ou ondes hertziennes sont des ondes électromagnétiques qui se propagent de deux façons : dans l espace libre (propagation rayonnée, autour de la Terre par exemple) dans des lignes (propagation guidée, dans un câble … Wikipédia en Français
PROPAGATION — s. f. Multiplication par voie de génération, de reproduction. La propagation du genre humain. La propagation de l espèce. On mit dans cette île déserte des animaux dont la propagation fut prodigieuse. Il s emploie figurément, et signifie,… … Dictionnaire de l'Academie Francaise, 7eme edition (1835)
Determination des constantes d'equilibre — Détermination des constantes d équilibre Les constantes d équilibre sont évaluées pour quantifier les équilibres chimiques à partir de mesures de concentrations, directes ou indirectes, et mettant en œuvre des techniques numériques. Cet article… … Wikipédia en Français
Détermination des constantes d'équilibre — Les constantes d équilibre sont évaluées pour quantifier les équilibres chimiques à partir de mesures de concentrations, directes ou indirectes, et mettant en œuvre des techniques numériques. Cet article se limite aux équilibres en solutions… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Équations des ondes électromagnétiques — Équations de Maxwell Ne doit pas être confondu avec Relations de Maxwell. Les équations de Maxwell, aussi appelées équations de Maxwell Lorentz, sont des lois fondamentales de la physique. Elles constituent les postulats de base de l… … Wikipédia en Français
Applications Des Satellites — Cet article décrit les diverses applications des satellites. Sommaire 1 Qu est ce qu un satellite artificiel ? 2 Les différents types de satellites artificiels 2.1 Satellite scientifique … Wikipédia en Français
Applications des satellites — Cet article décrit les diverses applications des satellites. Sommaire 1 Qu est ce qu un satellite artificiel ? 2 Les différents types de satellites artificiels 2.1 Satellite scientifique … Wikipédia en Français
LUMIÈRE - Histoire des idées — La lumière est facilement associée à une notion d’évidence et de simplicité dont elle reste le symbole. La Genèse affirme que la lumière fut créée le premier jour, précédant ainsi largement une complexité du monde sans cesse accrue. Pourtant ce… … Encyclopédie Universelle

Dictionnaires et Encyclopédies sur 'Academic'

Propagation des erreurs