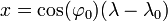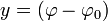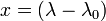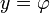- Projection cylindrique equidistante
-
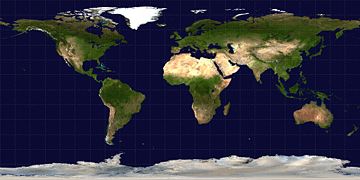
Projection cylindrique équidistante
La projection cylindrique équidistante, encore appelée projection équirectangulaire ou projection géographique, est un type de projection cartographique très simple attribué à Marinus de Tyr vers 100 ap. J.-C.[1]
Projection équidistante
Sommaire
Description
La projection consiste simplement à considérer les coordonnées polaires de latitude et longitude comme des coordonnées cartésiennes. En ce sens, on parle parfois de « non-projection ».
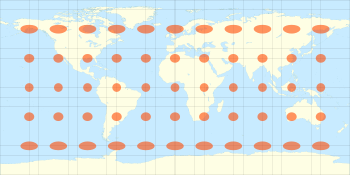
Cependant la transformation effectuée se définit (partiellement) comme une projection de la surface du globe sur la surface d'un cylindre, dont l'axe se confond avec l'axe des pôles et contient les origines des vecteurs de projection. Les méridiens sont alors projetés sur des lignes verticales espacées de manière égale, et les parallèles sont aussi projetés sur des lignes horizontales équidistantes (espacement horizontal constant). Ce dernier point différencie cette projection de la projection de Mercator. De plus, contrairement à la projection de Mercator, la projection cylindrique équidistante n'est pas conforme. Elle n'est pas non plus équivalente, mais aphylactique (elle conserve les distances le long des méridiens).
Définition mathématique
La projection cylindrique équidistante avec les indicatrix de déformation de Tissot.Les équations suivantes déterminent les coordonnées x et y d'un point de latitude φ et de longitude sur une carte à partir de sa latitude φ et de sa longitude λ lorsque le point (φ0, λ0) est au centre de la carte (fixé, par convention, à l'origine) :
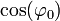est une constante ; la transformation est donc bilinéaire. Cette constante se traduit par à une absence de déformation à proximité du parallèle central (c'est-à-dire de latitude φ0), et minimise globalement la déformation.La projection plate carrée correspond au cas particulier où la carte est centrée sur l'équateur :
De manière plus restrictive, il s'agit d'une projection cylindrique équidistante du globe entier.
Utilisation
Représentation plate carrée de la France. La latitude relativement élevée de la France entraîne un étirement horizontal important. La carte est excentrée.À cause des distorsions introduites par cette projection, elle est de peu d'utilité pour la navigation ou les cartes cadastrales.
En revanche, sa simplicité fait que cette projection est privilégiée par les sites web de géolocalisation (Geoportail, Google maps, ...). En particulier, la plate carrée est devenue de-facto un standard car le rendu ne dépend plus du centre choisi. Malheureusement, on observe un étirement horizontal croissant lorsqu'on s'éloigne de l'équateur.
Notes et références de l'article
- ↑ Flattening the Earth: Two Thousand Years of Map Projections, John P. Snyder, 1993, pp. 5-8, ISBN 0-226-76747-7.
Voir aussi
Articles connexes
Liens et documents externes
- (en) The blue marble : land surface, ocean color and sea ice : réalisation de la projection équirectangulaire du globe terrestre à partir d'images satellites.
- (en) Tableau d'exemples et propriétés de toutes les projections communes, par radicalcartography.net.
- (en) Projection équirectangulaire panoramique, sur le wiki PanoTools.
Portail de la géodésie et de la géophysique
Portail de la géographie
Portail de l’astronomie
Catégorie : Projection cartographique
Wikimedia Foundation. 2010.
