- Poset
-
Un poset (de l'anglais partially ordered set, en français "ensemble partiellement ordonné") formalise la notion intuitive d'ordre ou d'arrangement entre les éléments d'un ensemble. Un poset est un ensemble muni d'une relation d'ordre qui indique que pour certains couples d'éléments, l'un est plus petit que l'autre. Tous les éléments ne sont pas forcément comparés, contrairement au cas d'un ensemble muni d'un ordre total.
Si l'ensemble est fini, on dispose d'une représentation graphique du poset, le diagramme de Hasse, ce qui peut permettre de travailler plus aisément dessus. Si l'ensemble est infini, on peut dessiner une partie de son diagramme de Hasse.
Sommaire
Définition et exemples
Définition
Un ordre (ou ordre partiel) est une relation binaire sur un ensemble P qui est réflexive, antisymétrique et transitive.
Ce n'est donc pas nécessairement un ordre total.
Exemples
- L'ensemble des nombres entiers naturels, muni de la divisibilité est un poset infini
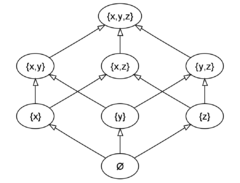
- L'ensemble des parties d'un ensemble donné, muni de l'inclusion forme un poset. Si l'ensemble donné est fini, son ensemble des parties est fini (plus précisément pour
, on a 
). La figure ci-dessous représente le diagramme de Hasse d'un ensemble à 3 éléments.
- L'ensemble des nombres complexes muni de la relation d'ordre suivante est partiellement ordonné :
.
Par exemple, on ne peut pas comparer 1 et i. Cet ordre n'est pas compatible avec la structure de corps de
.- L'ensemble des fonctions de
dans , muni de la relation d'ordre f < g si 
, est un poset infini. Intuitivement, une fonction est plus petite qu'une autre si sa courbe est toujours en dessous de l'autre courbe. On peut généraliser cet exemple aux fonctions d'un ensemble X dans un poset P. - L'ensemble des partitions d'un ensemble donné est partiellement ordonné, avec l'ordre donné par le raffinement des partitions : par définition, une partition est plus fine qu'une autre si elle fractionne les parties de l'autre en de plus petites parties.
- On peut munir R[X1,...,Xn] l'ensemble des polynômes à n variables d'une relation d'ordre partiel. On commence par comparer les monômes à n variables via l'ordre lexicographique induit par 1 < X1 < X2 < ... < Xn (cet ordre lexicographique est total). On compare deux polynômes P et Q en disant que P est strictement plus petit que Q si tout monôme non nul de P est strictement plus petit que tout monôme non nul de Q. Cette relation d'ordre sur les polynômes est partielle.
Spécificités des ensembles partiellement ordonnés
Plus grand élément et élément maximal
Si E est un poset, il n'existe pas forcément de plus grand élément. Si E est un poset fini, il contiendra un (ou plus) élément maximal. Si E est un ensemble inductif infini, on peut utiliser le lemme de Zorn pour avoir l'existence d'un élément maximal.
Certaines conditions sur les plus grands éléments et plus petits éléments d'un poset conduisent à la définition d'un treillis.
Liens avec les complexes simpliciaux
Une classe importante de complexes simpliciaux provient de posets finis. On définit le complexe d'ordre D(P) d'un poset fini P comme étant l'ensemble des chaînes de P. Le complexe d'ordre est trivialement un complexe simplicial.
L'étude du poset donne des informations sur son complexe d'ordre, et donc il est intéressant d'étudier un complexe simplicial comme le complexe d'ordre d'un poset.
Finitude locale
Un poset E est dit localement fini si pour tous
, l'intervalle [x,y] est fini. Cette hypothèse permet de généraliser la formule d'inversion de Möbius.Références
Richard P. Stanley, Enumerative Combinatorics, vol.1, Cambridge Studies in Advanced Mathematics 49, Cambridge University Press, ISBN 0-521-66351-2
Voir aussi
Wikimedia Foundation. 2010.
