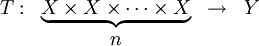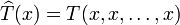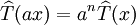- Polynome homogene
-
Polynôme homogène
En mathématiques, un polynôme homogène est un polynôme dont les termes sont des monômes dont le degré est le même, ou bien ses éléments ont la même dimension.
Sommaire
Exemples
- Exemple 1.
- x5 + 2x3y2 + 9x1y4
La somme des exposants est 5 pour chacun des monômes, donc il s'agit d'un polynôme homogène.
- Exemple 2.
Un polynôme homogène peut être construit à partir d'un tenseur d'ordre n. Si X est un espace vectoriel et Y un autre espace, alors, pour le tenseur T:
le polynôme homogène
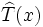de degré n associé à T estIl est apparent qu'un polynôme homogène est une fonction homogène de degré n. Pour le scalaire a, on a
qui découle de la multi-linéarité du tenseur.
Formes
Quadratique
La théorie des formes quadratiques a de nombreuses applications en mathématiques et en physique théorique. Pour n= 2, le tenseur est simplement une matrice. Une forme quadratique est un polynôme homogène.
Algébrique
La forme algébrique ou plus simplement forme désigne également un polynôme homogène. Elle généralise la forme quadratique au degré 3 et plus, et étaient connu par le passé comme des quintiques. Pour désigner une forme particulière, il fallait à la fois donner son degré et le nombre de variables n. Une forme est sur un champ K, si elle applique Kn à K.
Une forme sur un champ K à n variables représente 0 s'il existe un élément
- (x1,...,xn)
dans Kn tel que au moins l'un des
- xi (i=1,...,n)
est différent de zéro.
Histoire
Les formes algébriques jouent un rôle important dans les mathématiques du XIXe siècle. Elles sont utilisées en géométrie projective et en théorie des nombres. L'utilisation en géométrie se justifie par la théorie des invariants. Il existe un groupe général linéaire qui agit sur n'importe quel espace de quintiques, et cette action de groupe pourrait aider à classifier quelques variétés algébriques (par exemple une hypersurface cubique pour n'importe quel nombre de variables).
Au XXIe siècle,, l'espace des quintiques est identifié aux tenseurs symétriques d'un certain degré construits à partir d'une puissance de tenseur dans un espace vectoriel V de dimension m. (C'est une application directe si nous travaillons sur un champ de caractéristique zéro). Pour cela, il faut calculer le produit du tenseur n-plis V avec lui-même et prendre le sous-espace de l'invariant selon le groupe symétrique qui permute les facteurs. Cette définition montre comment GL(V) agit.
En géométrie algébrique, il serait possible d'étudier l'orbite de groupe de cette action. Plus précisément, les orbites de l'action sur l'espace de projection contenant l'espace vectoriel des tenseurs symétriques. La construction des invariants serait la théorie des anneaux de coordonnées sur l'espace des orbites, en faisant l'hypothèse qu'un tel espace existe. Il a fallu attendre la théorie de l'invariance géométrique de David Mumford pour avoir une réponse constructive à ce problème. Auparavant, les invariants des quantiques étaient étudiés sans support théorique.
Pour les formes algébriques avec coefficients entiers, le désir de généraliser les résultats sur les formes quadratiques aux formes de degrés supérieurs motivait les recherches.
Voir aussi
Portail des mathématiques
Catégories : Polynôme | Algèbre | Géométrie algébrique
Wikimedia Foundation. 2010.
