Point critique (mathématiques)

Point critique (mathématiques)

En analyse à plusieurs variables, un point critique d'une fonction de plusieurs variables, à valeurs numériques, est un point d'annulation de son gradient. Les points critiques servent d'intermédiaire pour la recherche des extremums d'une telle fonction.

Plus généralement, on peut définir la notion de point critique d'une application différentiable entre deux variétés différentielles ; il s'agit des points où la différentielle n'est pas de rang maximal.

Points critiques et points d'extremums d'une fonction numérique

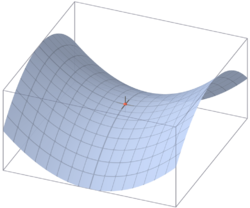Un point-selle (ou point-col) est un point critique.
Articles détaillés : matrice hessienne et gradient.

Soit f une fonction de n variables x1,...,xn, à valeurs réelles, différentiable sur un ouvert U. On dit qu'elle admet un point critique en un point u de U quand son gradient est nul en ce point.

Notamment, si u est un point d'extremum local de f c'est un point critique. La réciproque est fausse : une fois qu'on a déterminé les points critiques d'une fonction, il faut examiner leur nature, par exemple en effectuant le calcul de la matrice hessienne de f.

Exemple  :

Soit la fonction représentée à droite,

f:\begin{array}{rcl} \R^2 & \to & \R \\ (x,y) & \mapsto & z=x^2-y^2\end{array}

L'expression de son gradient est :

\nabla f = \begin{bmatrix}\frac{\part f}{\part x} \\ \frac{\part f}{\part y}\end{bmatrix} = \begin{bmatrix}2x\\-2y\end{bmatrix}

Il s'annule donc uniquement en (0,0), qui est le seul point critique. Pour déterminer la nature de ce dernier, calculons la matrice hessienne de la fonction :

\nabla^2f=\begin{bmatrix}\frac{\part^2 f}{\part x^2} & \frac{\part^2 f}{\part x\part y} \\ \frac{\part^2 f}{\part x\part y} & \frac{\part^2 f}{\part y^2}\end{bmatrix} = \begin{bmatrix}2&0\\0&-2\end{bmatrix}

Elle a pour valeurs propres 2 et -2. Elle n'est donc ni positive, ni négative : il s'agit d'un point-selle.

Points et valeurs critiques pour une application entre variétés

Soit f une application différentiable entre deux variétés M et N. On dit que f présente un point critique au point m si l'application linéaire tangente à f en m est non surjective (c'est-à-dire f n'est pas une submersion).

On appelle valeurs critiques les images des points critiques par f. Le théorème de Sard assure que pour une fonction indéfiniment différentiable, l'ensemble des valeurs critiques est de mesure nulle.

Voir aussi


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Point critique (mathématiques) de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Point critique (mathematiques) — Point critique (mathématiques) En analyse à plusieurs variables, un point critique d une fonction de plusieurs variables, à valeurs numériques, est un point d annulation de son gradient. Les points critiques servent d intermédiaire pour la… …   Wikipédia en Français

  • Point critique — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. en thermodynamique le point critique est une notion liée aux transitions de phase en mathématiques, le point critique est un concept de calcul… …   Wikipédia en Français

  • Point-col — Le point en rouge est un point col pour la fonction (ici la fonction z=x2−y2). En mathématiques, un point col (en anglais saddle point) pour une fonction f de plusieurs variables à valeurs dans …   Wikipédia en Français

  • Point selle — Point col Le point en rouge est un point col pour la fonction (ici la fonction z=x2−y2). En mathématiques, un point col (en anglais saddle point) pour une fonction f de plusieurs variables à valeurs dans …   Wikipédia en Français

  • Point — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Point », sur le Wiktionnaire (dictionnaire universel) Le terme point est utilisé dans divers domaines …   Wikipédia en Français

  • Critique — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Critique peut se référer à : la critique, l art de juger les œuvres de l esprit ; une critique, dans la presse écrite, article rédigé par un… …   Wikipédia en Français

  • Point col — Le point en rouge est le point du graphe de la fonction associé à son unique point selle (0,0). En mathématiques, un point selle (en anglais saddle point) d une fonction f définie sur un produit cartésien …   Wikipédia en Français

  • Critique De La Raison Pure — Première de couverture de la Kritik der reinen Vernunft Critique de la Raison pure Auteur Emmanuel Kant …   Wikipédia en Français

  • Critique de la Raison Pure — Première de couverture de la Kritik der reinen Vernunft Critique de la Raison pure Auteur Emmanuel Kant …   Wikipédia en Français

  • Critique de la Raison pure — Première de couverture de la Kritik der reinen Vernunft Critique de la Raison pure Auteur Emmanuel Kant …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”