Phenomene de Gibbs

Lors de l'étude des séries de Fourier et des transformées de Fourier, il apparaît parfois une déformation du signal, connue sous le nom de phénomène de Gibbs. Ce phénomène est un effet de bord qui se produit à proximité d'une discontinuité, lors de l'analyse d'une fonction dérivable par morceaux.

Sommaire 1 Histoire 2 Description du phénomène 3 Liens avec la causalité 4 Notes et références 5 Voir aussi 5.1 Articles connexes 6 Bibliographie

Histoire

Le phénomène fut mis pour la première fois en évidence en 1848 par Wilbraham^[1], mais cette découverte ne connut guère d'écho.

En 1898, Albert Michelson développa un système mécanique capable de calculer et sommer la série de Fourier d'un signal donné en entrée. Il observa alors un effet d'amplification des discontinuités, qui persistait malgré l'augmentation du nombre de coefficients calculés.

Alors que Michelson soupçonnait un défaut dans la fabrication de son engin, Gibbs montra que le phénomène était d'origine mathématique et se produisait dans des conditions très générales^[2]. En 1906, Maxime Bôcher donna la première interprétation satisfaisante du phénomène^[3] auquel il donna le nom de phénomène de Gibbs.

Description du phénomène

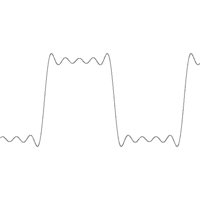
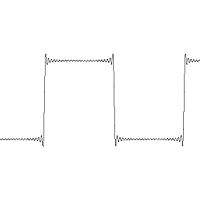
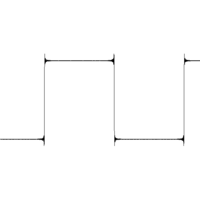
Phénomène de Gibbs

Approximation du créneau à l'ordre 10

Approximation du créneau à l'ordre 50

Approximation du créneau à l'ordre 250

Le phénomène de Gibbs est, en quelque sorte, un « défaut d'approximation » pour une fonction continue de classe C1 par morceaux. Pour une telle fonction f, le théorème de Dirichlet assure que la série de Fourier de f converge simplement vers la fonction f sur l'intervalle où f est C1 par morceaux. En tout point x de continuité la somme de la série de Fourier est f(x).

Le polynôme trigonométrique n-ième terme de la série de Fourier, S_n(f), est une fonction continue, il est donc normal qu'il ne puisse approcher uniformément la fonction aux points de discontinuité. Précisément, sur un segment sur lequel f est dérivable, on observe une convergence uniforme, conformément au théorème de Weierstrass trigonométrique (c'est le cas des zones de « plateau » dans l'exemple de la fonction créneau).

Au niveau du point de discontinuité x, S_n(f) subit une forte oscillation, une sorte de « ressaut » qui se mesure en comparant les valeurs en 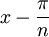et 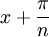. En effet, toujours d'après le théorème de Dirichlet, la série de Fourier de f converge aussi simplement aux points de discontinuités mais vers la régularisée de Dirichlet, ie la demi-somme des valeurs de f de part et d'autre du point de dicontinuités. Lorsque n devient grand, l'amplitude de ces oscillations tend vers une limite strictement plus grande que l'amplitude de la discontinuité, alors que la largeur de la zone d'oscillation tend vers 0.

Il est remarquable que le phénomène s'exprime quantitativement de façon indépendante de la fonction considérée. Si la fonction a une discontinuité d'amplitude Δy, alors S_n(f), tout en restant continue, connaitra un « ressaut » en ordonnée valant de l'ordre de 18% de plus au voisinage de la discontinuité.

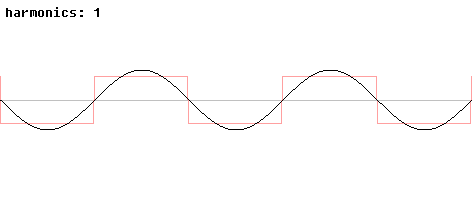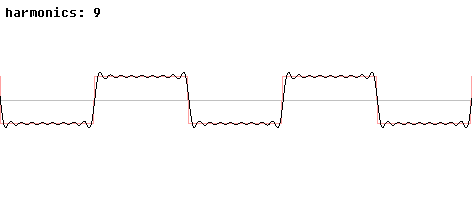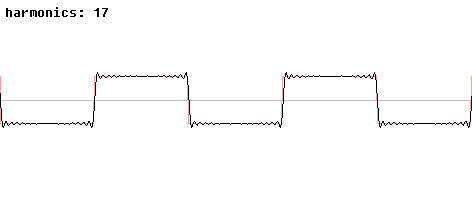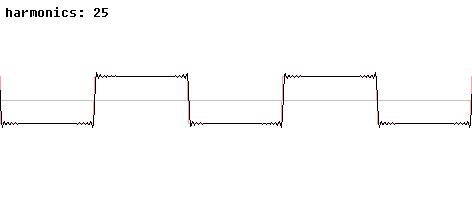
Liens avec la causalité

Les appareils de mesure se comportent comme des filtres passe-bas : ils sont incapables de réagir à des signaux de trop haute fréquence. Supposons que l'on mesure un échelon de tension : il sera déformé et fera apparaître des oscillations avant et après la discontinuité du signal réel.

Cependant, cela signifierait que les oscillations se sont produites avant que l'échelon ne soit mesuré, ce qui briserait la causalité. En réalité, cela peut avoir deux interprétations : soit les appareils ne sont pas des filtres parfaits (ce qui est compréhensible), soit l'échelon de tension ne peut être parfaitement discontinu.

Si on considère l'une ou l'autre de ces corrections, la transformée de Fourier est simplement décalée : les oscillations débutent au moment où l'échelon est envoyé, l'échelon n'étant observé qu'après un léger retard.

Notes et références

Voir aussi

Articles connexes

• Série de Fourier ;
• Phénomène de Runge ;
• Transformée de Fourier ;
• Traitement du signal ;
• Convergence simple ;
• Somme de Fejér ;
• Signal carré.

Bibliographie

• (en) Antoni Zygmund, Trigonometrical series, Dover publications, 1955.

• Portail des mathématiques