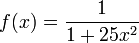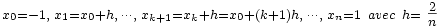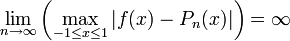Phénomène de runge

Phénomène de Runge

La courbe rouge est la fonction de Runge ; la courbe bleue est le polynôme interpolateur de degré 5 et la courbe verte est le polynôme interpolateur de degré 9. L'approximation est de plus en plus mauvaise.

Dans le domaine mathématique de l'analyse numérique, le phénomène de Runge se produit dans certains problèmes d'interpolation de fonctions lorsqu'on augmente le nombre de points d'interpolation. Il montre que cette augmentation ne constitue pas nécessairement une bonne stratégie d'approximation de la fonction.

Par définition, dans un problème à n points d'interpolations, le polynôme d'interpolation doit coïncider avec la fonction en chacun des n points et peut être de degré aussi élevé que n-1. Lorsque n augmente, on pourrait s'attendre à ce que fonction et polynôme d'interpolation deviennent de plus en plus proches. Cependant le mathématicien Carle David Tolmé Runge découvrit en étudiant l'erreur d'approximation entre une fonction et ses polynômes interpolateurs qu'ils pouvaient au contraire s'écarter de plus en plus fortement.

Exemple où le phénomène de Runge se produit

Considérons la fonction suivante :

$f(x) = \frac{1}{1+25x^2}$

On considère $(n + 1)$ points équirépartis dans le segment $[ - 1,1]$ :

$\scriptstyle x_0 = -1, \; x_1 = x_0 + h, \; \cdots, \; x_{k+1} = x_k + h = x_0 + (k+1)h, \; \cdots, \; x_n = 1 \ avec \ h = \textstyle \frac{2}{n}$

Enfin, on considère le polynôme interpolateur de f aux points $(x i)$ , c'est-à-dire l'unique polynôme $P$ de degré inférieur ou égal à n tel que $P (x i) = f (x i)$ pour tout i. On note $P n$ ce polynôme.

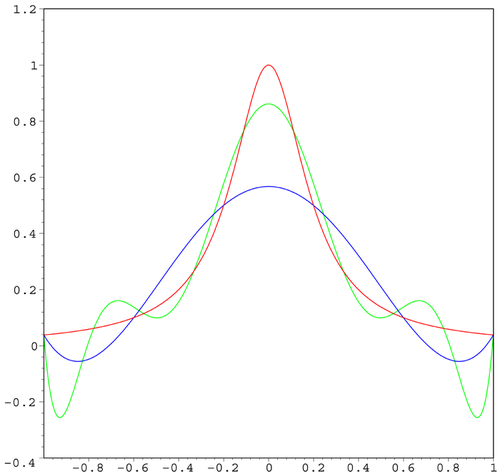
Runge a montré que l'erreur d'interpolation entre $P n$ et f tend vers l'infini lorsque n augmente. Autrement dit, plus on fixe de points où le polynôme a la même valeur que f, moins bien on approche la fonction ! Formellement

$\lim_{n \rightarrow \infty} \left( \max_{-1 \leq x \leq 1} | f(x) -P_n(x)| \right) = \infty$

En fait, lorsqu'on augmente le nombre de points, on constate que le polynôme se met à osciller fortement entre les points $x i$ avec une amplitude de plus en plus grande, comme l'illustre la figure.

Solutions au problème posé par le phénomène de Runge

On peut minimiser l'oscillation des polynômes interpolateurs en utilisant les points de Tchebychev au lieu de points équirépartis pour interpoler. Dans ce cas, on peut montrer que l'erreur d'interpolation (c'est-à-dire 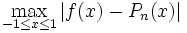$\max_{-1 \leq x \leq 1} | f(x) -P_n(x)|$ ) décroît lorsque n augmente.

Le phénomène de Runge met en lumière le fait que l'interpolation polynomiale n'est pas bien adaptée à l'approximation de fonctions. Pour approcher une fonction avec des polynômes, on peut préfèrer utiliser des splines par exemple (ce sont des polynômes par morceaux). Dans ce cas, pour améliorer l'approximation, on augmente le nombre de morceaux et non le degré des polynômes.

Voir aussi

On pourra comparer le phénomène de Runge au phénomène de Gibbs qui se produit lorsqu'on interpole des fonctions par des polynômes trigonométriques.

Portail des mathématiques

Ce document provient de « Ph%C3%A9nom%C3%A8ne de Runge ».

Catégorie : Interpolation numérique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Phénomène de runge de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Phenomene de Runge — Phénomène de Runge La courbe rouge est la fonction de Runge ; la courbe bleue est le polynôme interpolateur de degré 5 et la courbe verte est le polynôme interpolateur de degré 9. L approximation est de plus en plus mauvaise. Dans le domaine … Wikipédia en Français
Phénomène de Runge — La courbe rouge est la fonction de Runge ; la courbe bleue est le polynôme interpolateur de degré 5 et la courbe verte est le polynôme interpolateur de degré 9. L approximation est de plus en plus mauvaise. Dans le domaine mathématique de l… … Wikipédia en Français
Phenomene de Gibbs — Phénomène de Gibbs Lors de l étude des séries de Fourier et des transformées de Fourier, il apparaît parfois une déformation du signal, connue sous le nom de phénomène de Gibbs. Ce phénomène est un effet de bord qui se produit à proximité d une… … Wikipédia en Français
Phénomène de gibbs — Lors de l étude des séries de Fourier et des transformées de Fourier, il apparaît parfois une déformation du signal, connue sous le nom de phénomène de Gibbs. Ce phénomène est un effet de bord qui se produit à proximité d une discontinuité, lors… … Wikipédia en Français
Phénomène de Gibbs — Lors de l étude des séries de Fourier et des transformées de Fourier, il apparaît parfois une déformation du signal, connue sous le nom de phénomène de Gibbs. Ce phénomène est un effet de bord qui se produit à proximité d une discontinuité, lors… … Wikipédia en Français
Carl Runge — Carl David Tolmé Runge, né le 30 août 1856 et mort le 3 janvier 1927, fut un mathématicien et physicien allemand. Il a co développé avec Martin Wilhelm Kutta une des méthodes de résolution numérique pour les équations… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Rho algorithme — En analyse numérique, le ρ algorithme est un algorithme non linéaire d accélération de la convergence d une suite numérique dû à Peter Wynn[1]. C est un algorithme analogue à l extrapolation de Richardson, mais basé sur une extrapolation par… … Wikipédia en Français
Interpolation Polynomiale — En mathématiques, en analyse numérique, l interpolation polynomiale est une technique d interpolation d un ensemble de données ou d une fonction par un polynôme. En d autres termes, étant donné un ensemble de points (obtenu, par exemple, à la… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Phénomène de runge