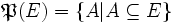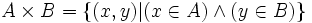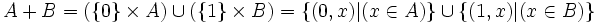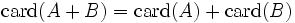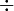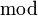Opérations sur les ensembles

Opération ensembliste

Les opérations ensemblistes sont les opérations mathématiques faites sur les ensembles, sans s’occuper de la nature des éléments qui composent ces ensembles. Les opérations booléennes (réunion, intersection, complémentaire ...) sont traitées dans l'article algèbre des parties d'un ensemble.

Ensemble des parties

L’ensemble des parties d'un ensemble E, noté habituellement 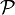$\mathcal{P}$ (E) ou 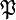$\mathfrak{P}$ (E), est, comme son nom l’indique, l’ensemble formé par tous les sous-ensembles de l’ensemble E:

$\mathfrak{P}(E) = \{ A | A \subseteq E \}$

Par exemple si A = {a,b}, 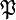$\mathfrak{P}$ (A)={Ø,{a},{b},A}

L’existence de l’ensemble des parties est assurée par un axiome, l’axiome de l'ensemble des parties. Cet axiome exprime en substance que pour tout ensemble E, il existe un ensemble F contenant tous les sous-ensembles de E.

L’unicité de l’ensemble des parties est assurée par un autre axiome, l’axiome d'extensionnalité.

L’ensemble des parties d’un ensemble, muni de la réunion, de l’intersection et de l’inclusion forme une algèbre de Boole.

L’ensemble des parties d’un ensemble, muni de la différence symétrique et de l’intersection forme un corps commutatif. Si l'ensemble de départ est fini, de cardinal n, alors ce corps est isomorphe à 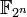$\mathbb{F}_{2^n}$ , corps fini à 2ⁿ éléments.

Produit cartésien

Le produit cartésien, noté 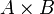$A \times B$ (lire « A croix B »), de deux ensembles A et B est l’ensemble des couples dont la première composante vient de A et la seconde de B :

$A \times B = \{ (x, y) | (x \in A) \wedge (y \in B) \}$

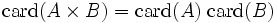
On a pour A et B finis: $\mathrm{card}(A \times B) = \mathrm{card}(A) \;\mathrm{card}(B)$

Somme disjointe

La différence symétrique de deux ensembles A et B ne doit pas être confondue avec leur somme disjointe, notée 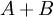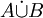$A + B \,$ , $A \dot\cup B \,$ ou encore $A \sqcup B$ :

$A + B = (\{ 0 \}\times A) \cup (\{ 1 \} \times B) = \{ ( 0, x) | (x \in A) \} \cup \{ ( 1, x) | (x \in B) \}\,$

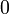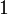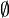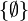Les symboles $0\,$ et $1\,$ dans la définition précédente peuvent être remplacés par d’autres, par exemple $\empty$ et $\{\empty\}$ . La seule exigence est que les deux symboles utilisés différent l’un de l’autre.

La somme disjointe a été conçue pour que, contrairement à la réunion, le cardinal de son résultat soit toujours la somme des cardinaux des ensembles concernés :

$\mathrm{card}( A + B ) = \mathrm{card}( A ) + \mathrm{card}( B)\,$

Elle peut être utilisée comme substitut à la notion de couple d’ensembles, surtout quand ces ensembles sont susceptibles d’être des classes.

Exponentiation

On définit 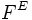$F^E \,$ comme l’ensemble des applications de $E$ dans $F$ .

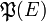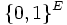On peut alors identifier l’ensemble des parties d’un ensemble $E$ , $\mathfrak P(E)$ , à $\{0,1\}^E \,$ ; cela revient en effet à identifier chaque partie de $E$ à son indicatrice.

On peut aussi considérer le produit cartésien 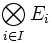$\bigotimes_{i\in I}E_i$ comme étant l’ensemble $E I$ .

Voir aussi

Algèbre des parties d'un ensemble
ensemblist, un jeu qui utilise les ensembles et les opérations boléennes, par géométrie de construction de solides.

Opérations binaires

Numériques	En ensemble ordonné	Structurelles	Autres

Élémentaires $+$ Addition $-$ Soustraction $\times$ Multiplication $\div$ Division $\hat{}$ Puissance Arithmétiques $div$ Quotient euclidien $\mod$ Reste euclidien $pgcd$ PGCD $ppcm$ PPCM Combinatoires $()$ Coefficient binomial $A$ Arrangement	Ensembles de parties $\cup$ Union $\backslash$ Complémentation $\cap$ Intersection $Δ$ Différence symétrique Ordre total $min$ Minimum $max$ Maximum Treillis $\wedge$ Borne inférieure $\vee$ Borne supérieure	Ensembles $\times$ Produit cartésien $\dot{\cup}$ Somme disjointe $\hat{}$ Puissance ensembliste Groupes $\oplus$ Somme directe $\ast$ Produit libre $\wr$ Produit en couronne Modules $\otimes$ Produit tensoriel $Hom$ Homomorphisme $Tor$ Torsion $Ext$ Extension Arbres $\vee$ Enracinement Variétés connexes $\#$ Somme connexe Espaces pointés $\vee$ Bouquet $\wedge$ Smash produit $\ast$ Joint	Fonctionnelles $\circ$ Composition de fonctions $\ast$ Produit de convolution Vectorielles $\cdot$ Produit scalaire $\wedge$ Produit vectoriel Algébriques $[,]$ Crochet de Lie ${,}$ Crochet de Poisson $\wedge$ Produit extérieur Homologiques $\smile$ Cup produit $\cdot$ Produit d'intersection Séquentielles $+$ Concaténation

Logique booléenne : $\land$ ET (conjonction) • $\lor$ OU (disjonction) • $\oplus$ OU exclusif • $\Rightarrow$ IMP (implication) • $\Leftrightarrow$ EQV (équivalence)

Portail des mathématiques

Ce document provient de « Op%C3%A9ration ensembliste ».

Catégories : Théorie des ensembles | Opération

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Opérations sur les ensembles de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Operations sur les ensembles — Algèbre des parties d un ensemble Cet article est consacré à une première approche des opérations sur les ensembles et de leurs propriétés : réunion, intersection, différence, complémentation, différence symétrique... Sommaire 1 Réunion 1.1… … Wikipédia en Français
Operations sur les bits — Opérations sur les bits Sommaire 1 Introduction 2 Opération conjonction (et) sur les bits 2.1 Présenter les entiers dans les ensembles fini 2.2 Propriétés … Wikipédia en Français
Opérations sur les bits — Sommaire 1 Introduction 2 Opération conjonction (et) sur les bits 2.1 Présenter les entiers dans les ensembles fini 2.2 Propriétés … Wikipédia en Français
Ensembles — Ensemble En théorie des ensembles, un ensemble désigne intuitivement une collection d’objets (les éléments de l ensemble), « une multitude qui peut être comprise comme un tout », comme l énonçait son principal initiateur, le… … Wikipédia en Français
Sur-ensemble — Sous ensemble L ensemble A est inclus dans l ensemble B. On dit que A est sous ensemble de B, ou que B est sur ensemble de A. En mathématiques, un ensemble A est un sous ensemble ou une partie d’un ensemble B, ou encore B est sur ensemble de A … Wikipédia en Français
ENSEMBLES (THÉORIE DES) - Théorie élémentaire — L’algèbre des ensembles et l’étude abstraite des relations sont d’une importance croissante dans toutes les disciplines qui cherchent à s’exprimer dans un cadre rigoureux. En mathématiques, c’est l’interrogation sur les fondements de cette… … Encyclopédie Universelle
ENSEMBLES (THÉORIE DES) - Théorie axiomatique — La théorie des ensembles fut créée par Georg Cantor à la fin du XIXe siècle. Cependant, le caractère extrêmement général et abstrait de la notion d’ensemble permit de produire des paradoxes rendant la théorie contradictoire (cf. théorie… … Encyclopédie Universelle
Congruence Sur Les Entiers — Pour les articles homonymes, voir Congruence. La congruence sur les entiers est une relation pouvant unir deux entiers. Elle fut pour la première fois étudiée en tant que structure par le mathématicien allemand Carl Friedrich Gauss à la fin du… … Wikipédia en Français
Congruence sur les entiers — Pour les articles homonymes, voir Congruence. La congruence sur les entiers est une relation pouvant unir deux entiers. Elle fut pour la première fois étudiée en tant que structure par le mathématicien allemand Carl Friedrich Gauss à la fin du… … Wikipédia en Français
Opérations ensemblistes — Opération ensembliste Les opérations ensemblistes sont les opérations mathématiques faites sur les ensembles, sans s’occuper de la nature des éléments qui composent ces ensembles. Les opérations booléennes (réunion, intersection, complémentaire … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Opérations sur les ensembles

Opération ensembliste

Sommaire

Ensemble des parties

Produit cartésien

Somme disjointe

Exponentiation

Voir aussi

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Opérations sur les ensembles

Opération ensembliste

Sommaire

Ensemble des parties

Produit cartésien

Somme disjointe

Exponentiation

Voir aussi

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link