- Opérateur à noyau
-
En analyse fonctionnelle, un opérateur à noyau est un exemple standard d'opérateur. Il se définit sur des espaces fonctionnels sur lesquels l'intégration a un sens, et au moyen de produit de convolution par des fonctions dépendant de paramètres. La famille de fonctions par lesquelles la convolution a lieu s'appellent le noyau de l'opérateur. Un opérateur à noyau S se met donc sous la forme :
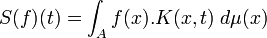
sans plus de précision sur le contexte, où t est un paramètre, f est la fonction à laquelle l'opérateur est appliqué et K le noyau de l'opérateur.
Suivant la situations, les domaines de définition des fonctions mises en jeu, et la régularité des fonctions intervenant dans les problèmes, les espaces fonctionnels peuvent être modifiés. Toutefois, dans un grand nombre de cas déjà intéressants en pratique, il existe une étude complète de l'analyse spectrale des opérateurs à noyaux. Par ailleurs, il est fréquent que les opérateurs à noyaux soient des opérateurs compacts, autrement dit envoient parties bornées sur parties relativement compactes.
Les opérateurs à noyaux interviennent dans les phénomènes de diffusion où interviennent classiquement des équations intégrales. L'existence et l'unicité des solutions trouvent des solutions avec l'alternative de Frédholm, lorsque cette dernière est applicable, ie lorsque l'opérateur à noyau est un opérateur compact.
- Portail des mathématiques
Catégories : Théorie des opérateurs | Espace de Hilbert
Opérateur à noyau
Wikimedia Foundation. 2010.
