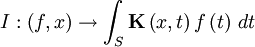- Operateur integral
-
En mathématiques, un opérateur intégral (qu'on nomme aussi transformée intégrale) est un opérateur qui se construit à partir d'intégrales, et qui regroupe de nombreuses transformées courantes, comme la transformée de Fourier, ainsi que la convolution.
On peut toujours écrire un opérateur intégral I sous la forme :
avec f une fonction, K une application, appelée « noyau » de l'opérateur et S un intervalle. Il est possible que l'intégrale ne converge pas, l'opérateur peut alors diverger.
Il existe souvent un opérateur intégral inverse, I-1, tel que I I-1 = Id. Il existe aussi parfois un opérateur différentiel qui inverse un opérateur intégral.
- Portail des mathématiques
Catégorie : Théorie des opérateurs
Operateur integral
Wikimedia Foundation. 2010.