Nonagone

Ennéagone régulier

Un ennéagone ou nonagone est un polygone à 9 sommets et à 9 côtés. Un tel polygone possède 27 diagonales. Enfin la somme de ses angles vaut 1260°.

Aire d'un ennéagone régulier

L'aire d'un ennéagone régulier vaut 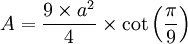, a étant un des 9 côtés de l'ennéagone.

Construction d'un ennéagone régulier

Un ennéagone régulier n'est pas constructible avec seulement une règle (non marquée) et un compas, car 9 ne satisfait pas la condition du Théorème de Gauss-Wantzel. Il l'est, par contre, "par neusis", avec une règle marquée et un compas.

régulier avec une règle marquée et un compas (méthode de J-C.Debuisser)

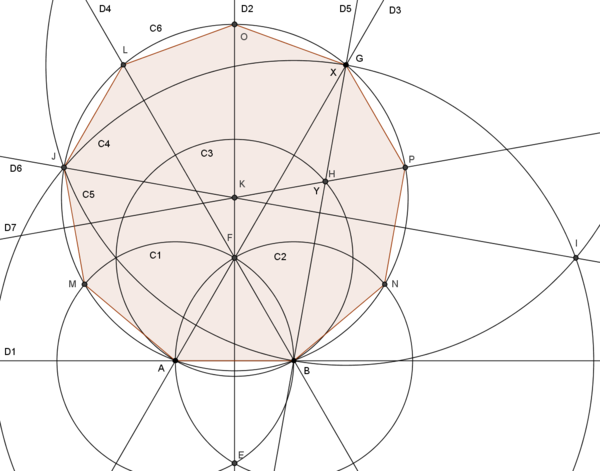
Pour construire un ennéagone régulier dont un des côtés est le segment AB, de longueur u, on procède ainsi :

• Appelons D1 la droite contenant A et B.
• Tracer les cercles C1 de centre A passant par B, et le cercle C2 de centre B passant par A. Ces deux cercles se coupent en deux points E et F, F étant le point du demi plan d'origine D1 dans lequel on veut situer le centre de l'énnéagone.
• Tracer la droite D2 passant par E et F.
• Tracer le cercle C3 de centre F passant par A.
• Tracer les droites D3 et D4, passant par F et, respectivement, par A et B.
• Marquer la règle de deux points X et Y distants de u égal au segment AB qui est le côté du triangle équilatéral.
• Faire glisser la règle marquée en pivotant autour du point B et en maintenant la marque X sur D3, avec la marque Y entre X et B, jusqu'à ce que Y se trouve sur le cercle C3, en un point H. La marque X se trouve alors en un point G sur la droite D3.
• Tracer le cercle C4 de centre B passant par G, et le cercle C5 de centre G passant par B. Ces deux cercles se coupent en I et J, J étant le point situé dans le demi plan d'origine D5 contenant A.
• Tracer la droite D6 passant par I et J. Elle coupe D2 en K.
• Tracer le cercle C6 de centre K passant par A. Il passe aussi par B, G et J.
• C6 coupe D2 en un point O dans le demi plan d'origine D1 contenant K.
• C6 coupe D4, C1 et C2, en des points autres que A ou B, respectivement en L, M et N.
• Tracer la droite D7 passant par K et H. Elle coupe C6 en P dans le demi plan d'origine D5 contenant N.
• Le polygone ABNPGOLJM est l'ennéagone recherché.

La démonstration complète est un peu longue mais relève de la géométrie élémentaire.

Voir aussi

• Nombre constructible

Liens externes

• Constructions approchées d'un ennéagone

• Animations pour des constructions approchées d'un ennéagone

• Autre construction approchée d'un ennéagone

• Portail de la géométrie