Nombre définissable

Un nombre définissable, nommé aussi parfois nombre accessible^[1], ou nombre nommable^[2], correspond à la notion intuitive décrite par Emile Borel ^[3] de « nombre pouvant être décrit comme un objet mathématique, de sorte que ceux qui en parlent soient assurés qu'ils parlent d'un même et unique nombre ».

Le besoin de cette notion est apparu devant le constat que quasiment tous les nombres réels sont aléatoires^[4] et que ceux-ci ne pourraient être désignés qu'en exprimant in-extenso leur développement numérique infini, ce qui est impossible. Ils ne peuvent donc être "définis" par une formule finie qui permettrait de l'identifier de manière unique.

Une définition informelle est insuffisante car menant à des difficultés, notamment par utilisation de l'argument diagonal (voir paragraphe "Problèmes soulevés par le concept informel de nombre définissable").

Le concept de "nombre définissable", tout comme celui de "proposition démontrable", n'est donc pas un concept absolu, mais doit se réfèrer à un langage ou un système formel utilisé pour définir ou nommer le nombre.

Un nombre (réel/complexe..) x est définissable dans un système formel S s'il existe une formule P(x) appartenant à S, dont on puisse démontrer - dans S - qu'il existe un et un seul x tel que P(x). La proposition P(x) ⇒ (x est nombre réel/complexe..) doit être démontrable dans S^{[réf. souhaitée]}.

P(x) est alors la définition de x dans S. Le système formel généralement utilisé pour définir les nombre est généralement la théorie ZF. Sans précision, un "nombre définissable" est un nombre définissable dans la théorie ZF.

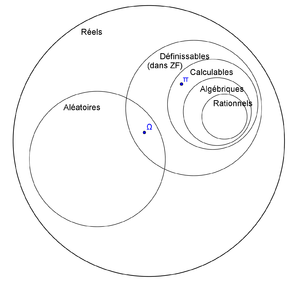
Il existe des nombres définissables mais non calculables, dont le représentant le plus significatif est le nombre Oméga de Chaitin.

Problèmes soulevés par le concept informel de nombre définissable

Considérer qu'il y a - dans l'absolu - deux catégories de nombres réels, à savoir ceux qui sont définissables et ceux qui ne le sont pas, conduit vite à des contradictions.

N'importe quelle suite infinie de décimales étant censée correspondre de manière univoque à un réel compris entre 0 et 1, l'intervalle [0,1] n'est pas un ensemble dénombrable, ce qui avait été démontré par l'argument de la diagonale de Cantor, et donc l'ensemble des réels ne l'est pas non plus.^[5]

Si maintenant on suppose qu'il existe un ensemble E des nombres réels définissables, alors, toute définition étant une suite finie d'éléments syntaxiques tirés d'un langage dénombrable, il paraît naturel de penser que les nombres réels définissables sont en infinité seulement dénombrable^[6]; cependant, on peut aussitôt appliquer le même argument diagonal pour définir un nouveau nombre réel µ non élément de E, et E ne serait donc pas l'ensemble des réels définissables, contradiction.

Ainsi, il est illusoire de vouloir définir un ensemble des nombres définissables, du moins sans le lier à un système formel.

Le concept de nombre définissable dans un système formel est immune à l'argument diagonal, car le nombre obtenu par diagonalisation n'est pas définissable dans le système formel initial.

Le fait qu'il existe des nombres non-définissables dans un système formel, mais qui le sont dans un autre système formel étendu est une forme d'incomplétude de cette notion, similaire à l'incomplétude de la démontrabilité.

Propriétés des nombres définissables dans ZF

Hiérarchie des nombres. Les surfaces ne sont ni à l'échelle, ni représentatives. Seules les relations d'inclusion/intersection sont représentatives.

• Les nombres définissables sont dénombrables. La mesure de l'ensemble des nombres réels définissables est nulle. En conséquence, la probabilité qu'un réel soit non définissable est de un.

• Un nombre calculable est définissable, mais la réciproque n'est pas nécessairement vraie.

Historique

Pythagore, qui ne laissa aucun écrit, était, selon la tradition, convaincu que tout se pouvait définir par les nombres et leurs rapports.

Il est supposé avoir sacrifié cent taureaux aux dieux dans sa joie d'avoir découvert le théorème qui porte son nom et par suite la preuve que les côtés d'un rectangle étaient incommensurables avec sa diagonale ^[7] ; en réalité il n'est pas certain, ni qu'il soit l'auteur de cette trouvaille^[8], ni qu'il ait effectué ce sacrifice^[9], ni qu'il ait été particulièrement heureux que certains « nombres » ne puissent être définis comme rapport de nombres entiers, ce qui, pour ce que l'on sait de sa doctrine, était censé révéler une imperfection dans l'harmonie du monde. ^[10] De fait, cette découverte réagit durablement sur la conception du « nombre » chez les grecs, et les conduisit à développer une algèbre à caractère géométrique, cherchant le plus possible à résoudre des équations « par la règle et le compas » - mais alors surgirent les problèmes transcendants....^[11]

L'invention du calcul différentiel et du calcul intégral permit d'écrire beaucoup de nombres transcendants sous forme d'expressions de longueur finie ; ainsi le rapport constant de la longueur du cercle à son diamètre peut se définir par .

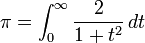Puis avec l'avènement de la théorie des ensembles, ses infinis différents et ses paradoxes sur la longueur des définitions, on commença à se poser des questions sur les fondements des mathématiques. Jean Cavaillès rapporte que jusque là, « la validité même des résultats, la structure interne de l'édifice n'étaient pas mises en question. Avec les paradoxes découverts entre 1890 et 1904, c'est au contraire à un danger menaçant la technique qu'il faut parer » ^[12].

La question du caractère non opérationnel du continu indénombrable se posa en particulier dans un débat au début du XX^e siècle entre Baire, Borel, Hadamard et Lebesgue, où au début le sujet était l'axiome de choix ; Lebesgue élargit le débat en contestant la validité des propositions portant sur des objets qui n'ont pas été définis. Hadamard se démarque de ses trois interlocuteurs en acceptant la construction cantorienne, alors que Baire par exemple refuse de considérer « l'ensemble des parties » d'un ensemble infini^[13]. Cependant, ces objections ne purent déboucher sur une théorie effective et quand Zermelo entreprit d'axiomatiser la théorie des ensembles, les idées de Cantor furent essentiellement préservées, ce qui entraînait l'indénombrabilité de .

Cette fois-ci, il semblait n'y avoir en vue aucun moyen de sauver l' « harmonie du monde ».... Une infinité non dénombrable de réels sont inaccessibles, leur existence seule étant connue. Et cependant, s'ils ne peuvent prétendre au statut d' objet mathématique défini, leur considération joue un rôle important, dit Borel, ^[14] qui y consacra son dernier ouvrage paru en 1952, dans la préface duquel il explique que, pour les êtres de raison tout comme pour les phénomènes physiques, on est amené à définir « une science de l'accessible et du réel, au-delà de laquelle il reste possible de développer une science de l'imaginaire et de l'imaginé ».^[15]

L'apparence des nombres réels, éloignée de leur origine

Après quelques commentaires sur le caractère « relativement inaccessible » des très grands nombres entiers, et donc des longues suites de décimales, Borel revient au chapitre II sur le concept général de nombre réel : tout nombre incommensurable résulte d'une division en deux classes du corps des nombres rationnels, sous la condition que tout élément de la première classe soit inférieur à tout élément de la seconde : c'est le principe des coupures de Dedekind.

Dans quelques cas simples, il est possible de préciser de quelle coupure il s'agit ; par exemple la coupure entre la classe des fractions p/q telles que q²-2p²<0 et celle des fractions p/q telles que q²-2p²>0 définit la racine carrée de 2. Mais dans l'immense majorité des cas, les propriétés que devrait avoir une telle division apparaissent comme extrêmement compliquées.

Borel remarque qu'il n'y a pas de méthode générale pour séparer en deux classes l'ensemble des rationnels compris entre 0 et 1 ; et quand on peut y arriver, c'est seulement parce que l'on connaît déjà une autre définition du nombre en question.

Homogénéité du continu et hétérogénéité du dénombrable

Borel montre que le calcul des probabilités peut être utilisé pour l'étude d'ensembles dont les éléments sont pour la plupart inaccessibles ; cependant parler de probabilité d'évènements appartenant à une classe dénombrable par rapport à un univers non dénombrable peut poser quelques problèmes. Le calcul des probabilités est dominé par la question du choix. Borel distingue deux sous-classes dans les mathématiques : il y a, selon lui, des mathématiques euclidiennes et des mathématiques zermeliennes ^[16]. Cette conception sera développée et illustrée tout au long de l'ouvrage et aboutira notamment au chapitre IX à l'exemple de ce qu'il appelle les ensembles ZD, duquel il déduit que l'axiome du choix est incompatible avec l'axiome euclidien d'après lequel deux figures superposables ont des propriétés identiques.^[17]

Notes et références

Voir aussi

Articles connexes

• Définition
• Oméga de Chaitin
• Théorie descriptive des ensembles

Lien externe

• La face cachée des nombres

• Portail des mathématiques