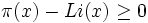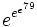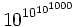Nombre De Skewes

En mathématiques et dans la théorie des nombres, le nombre de Skewes peut faire référence à plusieurs nombres extrêmement grands utilisés par le mathématicien sud-africain Stanley Skewes.

Par définition, le nombre est le plus petit nombre naturel x pour lequel

où 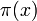est la fonction de compte des nombres premiers et Li(x), le logarithme intégral.

John Edensor Littlewood, le maître de Skewes, a démontré en 1914 qu'il existe un tel nombre (et donc, un premier nombre de cette sorte) et a trouvé que le signe de la différence 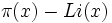change infiniment souvent. Qu'un tel nombre existe n'était pas tout à fait clair; en fait, toute l'évidence numérique alors disponible semblait suggérer que 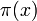est toujours inférieur à Li(x). La démonstration de Littlewood n'exhibait néanmoins pas un tel nombre x concret; elle n'était pas un résultat effectif.

Skewes démontra en 1933 qu'en supposant vraie l'hypothèse de Riemann, il existe un nombre x violant 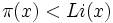au-dessous de

(mainteant quelquefois appelé premier nombre de Skewes), qui est approximativement égal à

.

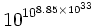En 1955, sans rien supposer sur l'hypothèse de Riemann, il est parvenu à démontrer qu'il doit exister une valeur de x au-dessous de

(quelquefois appelé deuxième nombre de Skewes).

Ces bornes supérieures (énormes) ont depuis été réduites considérablement. Sans rien supposer sur l'hypothèse de Riemann, H. J. J. te Riele en 1987 démontra que la borne supérieure de

.

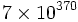Une meilleure estimation :

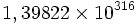découverte par Bays et Hudson (2000). La meilleure valeur pour le premier croisement est maintenant

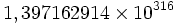(Demichel 2005). C'est avec une très grande confiance, la première occurrence de .

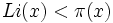La tâche de Skewes fut de rendre effective la démonstration d'existence de Littlewood : en exhibant une certaine borne supérieure concrète pour le premier changement de signe. Selon Georg Kreisel, ceci n'était pas considéré comme évident à cette époque, même en principe. L'approche appelée déroulement en théorie de la démonstration regarde directement les preuves et leurs structures pour produire les bornes. L'autre manière, plus souvent vue en pratique dans la théorie des nombres, change suffisamment la structure de la preuve de sorte que les constantes absolues peuvent être rendues encore plus explicites.

Le résultat de Skewes fut rendu célèbre en partie parce que la structure de la preuve utilisait le principe du tiers exclu, qui n'est pas a priori un argument constructif (il se divise en deux cas, et il n'est pas calculable dans le cas où il fonctionne).

Bien que les deux nombres de Skewes soient grands comparés à la plupart des nombres rencontrés dans les démonstrations mathématiques, ni l'un ni l'autre n'est proche du nombre de Graham.

Références

• J.E. Littlewood: "Sur la distribution des nombres premiers", Comptes Rendus 158 (1914), pages 1869-1872
• S. Skewes: "On the différence π(x) − Li(x)", Journal of the London Mathematical Society 8 (1933), pages 277-283
• S. Skewes: "On the différence π(x) − Li(x) (II)", Proceedings of the London Mathematical Society 5 (1955), pages 48-70
• H.J.J. te Riele: "On the différence π(x) − Li(x)", Math. Comp. 48 (1987), pages 323-328

Liens externes

• [pdf]li crossover pi.pdf