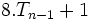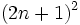Nombre octogonal centre

Nombre octogonal centre

Nombre octogonal centré

En mathématiques, un nombre octogonal centré est un nombre figuré centré qui représente un octogone avec un point au centre et tous les autres points entourant le centre en couches successives. Le nombre octogonal centré pour n est donné par la formule

8.T_{n-1}+1\,

où T est un nombre triangulaire régulier, ou plus simplement, en élevant au carré les nombres impairs :

(2n+1)^2\,

Les premiers petits nombres octogonaux centrés sont :

1, 9, 25, 49, 81, 121, 169, 225, 289, 361, 441, 529, 625, 729, 841, 961

Tous les nombres octogonaux centrés sont impairs, et en base 10, on peut noter que les derniers chiffres suivent le motif 1-9-5-9-1.

En calculant la fonction tau de Ramanujan pour un nombre octogonal centré, celle-ci fournit un nombre impair, alors que pour tout autre nombre, la fonction fournit un nombre pair.

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Nombre octogonal centr%C3%A9 ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre octogonal centre de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Nombre Octogonal Centré — En mathématiques, un nombre octogonal centré est un nombre figuré centré qui représente un octogone avec un point au centre et tous les autres points entourant le centre en couches successives. Le nombre octogonal centré pour n est donné par la… …   Wikipédia en Français

  • Nombre octogonal centré — En mathématiques, un nombre octogonal centré est un nombre figuré centré qui représente un octogone avec un point au centre et tous les autres points entourant le centre en couches successives. Le nombre octogonal centré pour n est donné par la… …   Wikipédia en Français

  • 1500 (nombre) — Nombres 1000 à 1999 Cet article recense la plupart des nombres qui ont des propriétés remarquables allant de mille (1000) à mille neuf cent quatre vingt dix neuf (1999). Article détaillé : 1000 (nombre). Sommaire 1 Nombres dans le 1er… …   Wikipédia en Français

  • 1988 (nombre) — Nombres 1000 à 1999 Cet article recense la plupart des nombres qui ont des propriétés remarquables allant de mille (1000) à mille neuf cent quatre vingt dix neuf (1999). Article détaillé : 1000 (nombre). Sommaire 1 Nombres dans le 1er… …   Wikipédia en Français

  • 2000 (nombre) — Nombres 2000 à 2999 Cet article recense la plupart des nombres qui ont des propriétés remarquables allant de deux mille (2 000) à deux mille neuf cent quatre vingt dix neuf (2 999). Sommaire 1 Nombres dans le 2e millier (2 000… …   Wikipédia en Français

  • 2004 (nombre) — Nombres 2000 à 2999 Cet article recense la plupart des nombres qui ont des propriétés remarquables allant de deux mille (2 000) à deux mille neuf cent quatre vingt dix neuf (2 999). Sommaire 1 Nombres dans le 2e millier (2 000… …   Wikipédia en Français

  • 2005 (nombre) — Nombres 2000 à 2999 Cet article recense la plupart des nombres qui ont des propriétés remarquables allant de deux mille (2 000) à deux mille neuf cent quatre vingt dix neuf (2 999). Sommaire 1 Nombres dans le 2e millier (2 000… …   Wikipédia en Français

  • 2006 (nombre) — Nombres 2000 à 2999 Cet article recense la plupart des nombres qui ont des propriétés remarquables allant de deux mille (2 000) à deux mille neuf cent quatre vingt dix neuf (2 999). Sommaire 1 Nombres dans le 2e millier (2 000… …   Wikipédia en Français

  • 2100 (nombre) — Nombres 2000 à 2999 Cet article recense la plupart des nombres qui ont des propriétés remarquables allant de deux mille (2 000) à deux mille neuf cent quatre vingt dix neuf (2 999). Sommaire 1 Nombres dans le 2e millier (2 000… …   Wikipédia en Français

  • 2200 (nombre) — Nombres 2000 à 2999 Cet article recense la plupart des nombres qui ont des propriétés remarquables allant de deux mille (2 000) à deux mille neuf cent quatre vingt dix neuf (2 999). Sommaire 1 Nombres dans le 2e millier (2 000… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”