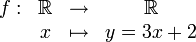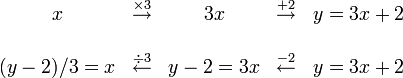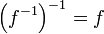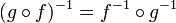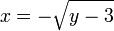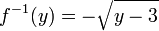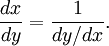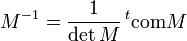Application réciproque

Pour les articles homonymes, voir Réciproque (homonymie).

En mathématiques, une application réciproque est en des termes simples une fonction qui « fait exactement l'inverse de ce que fait une application donnée ». L'application réciproque permet de retrouver un élément à partir de son image par une application donnée; autrement dit une application réciproque défait ce que l'application originale a fait.

Exemple

On considère la fonction

$\begin{matrix} f: & \R & \rightarrow & \mathbb R \\ & x & \mapsto & y = 3x+2 \end{matrix}$

Pour défaire ce qu'a fait f, on peut remarquer que f est composée de deux opérations élémentaires faciles à défaire

$\begin{matrix} x & \stackrel{\mathrm{\times 3}}\rightarrow& 3x& \stackrel{\mathrm{+ 2}}\rightarrow & y= 3x+2\\ \\ (y-2)/3=x &\stackrel{\mathrm{\div 3}}\leftarrow & y-2 =3x&\stackrel{\mathrm{-2}}\leftarrow& y = 3x+2 \end{matrix}$

Ainsi, en appliquant à y, la fonction 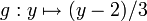$g:y\mapsto (y-2)/3$ , on défait ce que la fonction f avait fait. En langage mathématique cela s'écrit :

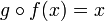
Pour tout réel x, $g\circ f (x) = x$

De même, en appliquant à un réel y la fonction g puis en appliquant au résultat la fonction f, on retrouve le réel y. En langage mathématique cela s'écrit :

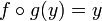
Pour tout réel y, $f\circ g (y) = y$

La fonction, définie sur un ensemble E, qui laisse invariants tous les éléments de E, se note $I d E$ . Les égalités précédentes s'écrivent donc :

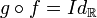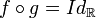
$g \circ f = Id_{\R}$ et $f \circ g = Id_{\R}$

On dit alors que g est l'application réciproque de f et on la note $f - 1$

L'exposant « -1 » n'est pas une puissance et $f - 1$ ne correspond pas à l'inverse d'une fonction pour la multiplication, mais à l'inverse pour la composition de fonctions.

Résultats généraux

Définition

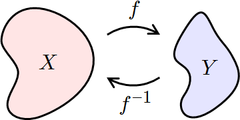
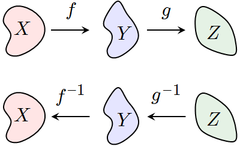
La réciproque de la fonction ƒ de X vers Y, est la fonction ƒ^–1 qui de Y retourne versX.

Si f est une application d'un ensemble X vers un ensemble Y et s'il existe une application g de Y vers X telle que :

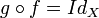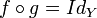$g \circ f = Id_{X}$ et $f \circ g = Id_{Y}$ ,

on appelle g l'application réciproque de f et on la note $f - 1$ .

L'existence d'une telle fonction g n'est possible que si f est bijective :

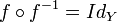
chaque élément de l'ensemble d'arrivée doit être atteint par f car $f \circ f^{-1} = Id_{Y}$
chaque élément de l'ensemble d'arrivée doit être atteint une seule fois par f car si f(a)=f(b) alors 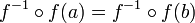$f^{-1} \circ f (a)= f^{-1} \circ f (b)$ et a = b.

Une telle application g est alors unique : c'est l'application qui, à tout élément y de Y, associe l'unique antécédent de y par f.

Propriétés

Réciproque de la réciproque

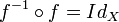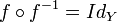La double propriété : $f^{-1} \circ f = Id_{X}$ et $f \circ f^{-1} = Id_{Y}$ montre que f est aussi l'application réciproque de $f - 1$ , c'est-à-dire que

$\left(f^{-1}\right)^{-1} = f$

Réciproque d'une composée

l'inverse de g o ƒ est ƒ^–1 o g^–1

La réciproque de la composée de deux fonction est donné par la formule

$(g \circ f)^{-1} = f^{-1} \circ g^{-1}$

Il faut remarquer que l'ordre de ƒ et g a été inversé; pour défaire ƒ suivi de g, il faut d'abord défaire g puis défaire ƒ.

Involution

Certaines application de E vers E sont leur propre réciproque, c'est le cas par exemple de

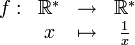
: $\begin{matrix} f: & \R^* & \rightarrow & \mathbb R^* \\ & x & \mapsto & \frac 1x \end{matrix}$

ou de toute symétrie orthogonale dans le plan.

De telles applications sont dites involutives.

Généralisation

Lorsque la fonction f n'est pas bijective, il est possible de définir une relation réciproque définie sur 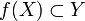$f(X) \subset Y$ qui à tout élément de f(X) associe ses antécédents par f. Si f n'est pas injective, la relation créée n'est pas une application, on parle alors de réciproque multiforme. Si f est injective, la relation ainsi créée est bien l'application réciproque de f restreinte à l'ensemble d'arrivée f(X).

Pour certaines fonctions f non surjectives, il existe une fonction g telle que 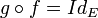$g \circ f = Id_E$ . Il suffit pour cela que f soit injective. On dit alors que g est un inverse à gauche pour f.

Pour certaines fonctions f non injectives, il existe une fonction g telles que 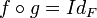$f \circ g = Id_F$ . Il suffit pour cela que f soit surjective (en admettant l'axiome du choix).

Réciproque d'une fonction numérique

Existence

Le théorème des valeurs intermédiaires et son corollaire, le théorème de la bijection, assurent que toute application continue strictement monotone sur un intervalle I détermine un bijection de I sur f(I) = J et que J est aussi un intervalle. Cela signifie qu'une telle fonction possède une application réciproque définie sur J à valeurs dans I.

Cette propriété permet la création de nouvelles fonctions définies comme application réciproque de fonctions usuelles.

Exemples

Fonction f(x)	Départ et arrivée	Fonction réciproque	Départ et arrivée	Notes
$f (x) = x n$	$[0;+\infty[ \to [0;+\infty[$	$f^{-1}(x)=\sqrt[n]x$	$[0;+\infty[ \to [0;+\infty[$	n entier naturel non nul
$f (x) = e x$	$\R \to ]0;+ \infty[$	$f - 1 (x) = ln(x)$	$]0;+ \infty[\to \R$
$f (x) = a x$	$\R \to ]0;+ \infty[$	$f - 1 (x) = log a (x)$	$]0;+ \infty[\to \R$	a réel strictement positif
$f (x) = x α$	$]0;+\infty[ \to ]0;+\infty[$	$f - 1 (x) = x 1 / α$	$]0;+\infty[ \to ]0;+\infty[$	$α$ réel non nul
$f (x) = sin(x)$	$[-\pi/2;\pi/2] \to [-1;1]$	$f - 1 (x) = arcsin(x)$	$[-1;1] \to [-\pi/2;\pi/2]$
$f (x) = cos(x)$	$[0;\pi] \to [-1;1]$	$f - 1 (x) = arccos(x)$	$[-1;1] \to [0;\pi]$
$f (x) = tan(x)$	$]-\pi/2;\pi/2[ \to \R$	$f - 1 (x) = arctan(x)$	$\R \to ]-\pi/2;\pi/2[$

À l'aide de ces fonctions, la recherche de l'application réciproque consiste à résoudre l'équation f(x) = y, d'inconnue x :

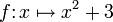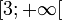La fonction $f \colon x \mapsto x^2+3$ est une bijection de $]- \infty;0]$ sur $[3;+\infty[$ et possède une application réciproque que l'on cherche à déterminer en résolvant l'équation :

x 2 + 3 = y

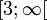
pour y dans $[3;\infty[$

x 2 = y - 3

puisque 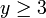$y \ge 3$ , cette équation possède deux solutions dont une seule appartenant à l'intervalle $]- \infty;0]$ :

$x=-\sqrt{y-3}$

Donc la réciproque de f est $f - 1$ définie par :

$f^{-1}(y)=-\sqrt{y-3}$

Cette recherche peut se révéler infructueuse et nécessiter la création d'une fonction nouvelle.

Graphe

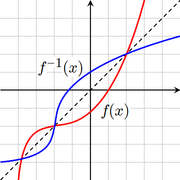
Courbes d'équations y = ƒ(x) et y = ƒ^–1(x). la droite en pointillés a pour équation y = x

Lorsque deux fonctions sont réciproques l'une de l'autre alors leurs représentations graphiques dans une plan muni d'un repère orthonormal sont symétriques l'une de l'autre par rapport à la droite (d) d'équation y = x.

En effet, si M(x ; y) est un point du graphe de f alors $y = f (x)$ donc $x = f - 1 (y)$ donc M'(y ; x) est un point du graphe de $f - 1$ . Or le point M'(y ; x) est le symétrique du point M(x ; y) par rapport à (d) pour les deux raisons suivantes :

Le milieu du segment [M M'] est sur la droite d'équation y = x, et d'autre part, le vecteur 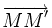$\overrightarrow{MM'}$ est orthogonal au vecteur de coordonnées (1 ;1), qui est un vecteur directeur de la droite d'équation y = x (leur produit scalaire canonique est nul).

On sait donc que s(M) est un point du graphe de $f - 1$ . Un raisonnement analogue prouve que si M est un point du graphe de $f - 1$ alors s(M) est un point du graphe de f.

Continuité

En général, la réciproque d'une fonction continue n'est pas continue mais la réciproque d'une fonction continue sur un intervalle I à valeurs dans un intervalle J est une fonction continue sur J. On trouve une démonstration dans l'article Théorème d'inversion locale.

Dérivabilité

Si f est une fonction continue sur un intervalle I à valeurs dans un intervalle J et si $f - 1$ est sa réciproque, la fonction $f - 1$ est dérivable en tout point b tant que f admet en $f - 1 (b)$ une dérivée non nulle. La dérivée en b de $f - 1$ est alors

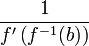$\frac{1}{f'\left(f^{-1}(b)\right)}$ .

Un moyen simple de comprendre, mais non de démontrer, ce phénomène est d'utiliser les notations différentielles et de remarquer que :

$\frac{dx}{dy} = \frac{1}{dy / dx} .$

On trouve une démonstration dans l'article Opérations sur les dérivées.

Exemple de réciproque de transformation du plan

Les transformations du plans sont les applications bijectives du plan, il est donc intéressant d'en connaitre les réciproques, du moins pour les transformations de références

Transformation	Transformation réciproque
Translation de vecteur 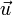$\vec u$	Translation de vecteur 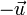$- \vec u$
Symétrie de centre O ou d'axe (d)	Symétrie de centre O ou d'axe (d)
Homothétie de centre C et de rapport k	Homothétie de centre C et de rapport 1/k
Rotation de centre C et d'angle θ	Rotation de centre C et d'angle - θ
Similitude directe de centre C, de rapport k et d'angle θ	Similitude directe de centre C, de rapport 1/k et d'angle - θ
Similitude indirecte de centre C, de rapport k et d'axe (d);	Similitude indirecte de centre C, de rapport 1/k et d'axe (d);
symétrie glissée d'axe (d) et de vecteur 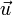$\vec u$	symétrie glissée d'axe (d) et de vecteur 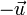$- \vec u$
affinité d'axe (d) de direction (d') et de rapport k	affinité d'axe (d) de direction (d') et de rapport 1/k

Réciproque en algèbre linéaire

En algébre linéaire un morphisme de groupe, d'anneau, de corps, d'espace vectoriel bijectif admet une application réciproque qui est aussi un morphisme de même type. L'application et sa réciproque sont appelés des isomorphismes.

Dans le cas d'une application f linéaire d'un espace vectoriel E vers un espace vectoriel F, tous deux de dimension finie. f admet une application réciproque si et seulement si E et F ont même dimension et si la matrice M de f dans les bases $(B 1, B 2)$ est inversible. La réciproque de f possède alors pour matrice dans la base $(B 2, B 1)$ la matrice note $M - 1$ appelée matrice inverse de M et valant

$M^{-1}=\frac1{\det M} \, {}^t{{\rm com} M}$

où det (M) est le déterminant de la matrice M et où $t com M$ est la transposée de la comatrice de M

Théorème d'inversion locale

Article détaillé : Théorème d'inversion locale.

Le théorème d'inversion locale précise les conditions d'existence locale d'une application réciproque pour une fonction f. C'est une généralisation d'un théorème simple sur les fonctions de la variable réelle.

Si f est définie sur un intervalle I et si a est un élément de I, si f possède en a une dérivée non nulle alors il existe un intervalle autour de a,

I a

, et un intervalle autour de f(a),

J f (a)

et une fonction

f - 1

définie sur

J f (a)

qui soit l'application réciproque de f restreinte à

I a

. Cette application réciproque est aussi dérivable en f(a).

Le théorème d'inversion locale généralise cette propriété a des fonctions définies sur des espaces vectoriels réels de dimension finie, de classe $C k$ . La condition f'(a) non nulle est alors remplacée par le jacobien de f en a est non nul.

Voir aussi

Liens internes

Liens externes

Fonction réciproque d'une fonction numérique (IUFM de la Réunion)

Portail des mathématiques

Ce document provient de « Application r%C3%A9ciproque ».

Catégories : Théorie des ensembles | Analyse

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Application réciproque de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Application Réciproque — Pour les articles homonymes, voir Réciproque (homonymie). En mathématiques, une application réciproque est en des termes simples une fonction qui « fait exactement l inverse de ce que fait une application donnée ». L application… … Wikipédia en Français
Application reciproque — Application réciproque Pour les articles homonymes, voir Réciproque (homonymie). En mathématiques, une application réciproque est en des termes simples une fonction qui « fait exactement l inverse de ce que fait une application donnée » … Wikipédia en Français
réciproque — [ resiprɔk ] adj. et n. • 1380; lat. reciprocus I ♦ Adj. 1 ♦ Qui s exerce à la fois d un premier terme à un second et du second au premier (d une même relation, d un même rapport). ⇒ symétrique. Relations réciproques. ♢ Spécialt Qui implique,… … Encyclopédie Universelle
Application (Mathématiques) — Pour les articles homonymes, voir Application. Graphique d une fonction … Wikipédia en Français
Application (mathematiques) — Application (mathématiques) Pour les articles homonymes, voir Application. Graphique d une fonction … Wikipédia en Français
Application (mathématique) — Application (mathématiques) Pour les articles homonymes, voir Application. Graphique d une fonction … Wikipédia en Français
Reciproque (homonymie) — Réciproque (homonymie) Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Application (mathématiques) — Pour les articles homonymes, voir Application. Pour les applications des mathématiques à d autres domaines, voir « Mathématiques appliquées » … Wikipédia en Français
Application composée — Composition de fonctions En mathématiques, la composition de fonctions (ou composition d applications) est un procédé qui consiste, à partir de deux fonctions, d en construire une nouvelle. Pour cela on utilise les images de la première fonction… … Wikipédia en Français
Réciproque (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Réciproque (homonymie) », sur le Wiktionnaire (dictionnaire universel) En mathématiques : En… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Application réciproque

Application réciproque

Sommaire

Exemple