Theoreme de la bijection

Théorème de la bijection

En analyse réelle, on appelle théorème de la bijection un corollaire du théorème des valeurs intermédiaires prouvant l'existence d'une bijection entre deux ensembles. Cette version se complète dans le supérieur par des propriétés touchant la réciproque de la bijection ainsi obtenue .

Sommaire

1 Corollaire du théorème des valeurs intermédiaires
- 1.1 Remarques
- 1.2 Utilisation pratique
2 Homéomorphisme
3 Notes et références

Corollaire du théorème des valeurs intermédiaires

Théorème de la bijection (version 1) — Si f est une fonction de $\R$ dans $\R$ continue et strictement monotone sur un intervalle I= [a;b] alors f détermine une bijection de [a;b] vers un intervalle J dont les bornes sont f(a) et f(b).

Démonstration du théorème

Ce théorème s'appuie explicitement sur lethéorème des valeurs intermédiaires et sur les propriétés liées à la monotonie de f. On suppose f croissante sur [a ;b], (une démonstration analogue est réalisable pour f décroissante).

Puisque f est strictement croissante sur [a;b] on sait que f(x) appartient à [f(a);f(b)]. En effet, comme a ≤ x ≤ b et que f est croissante on a f(a) ≤ f(x) ≤ f(b);
Soit y un élément de [f(a);f(b)], il s'agit de prouver que que y possède un unique antécédent dans [a;b]
- Comme f est continue sur [a;b] et que y appartient à [f(a);f(b)], le théorème des valeurs intermédiaires prouve qu'il existe au moins un réel x dans [a;b] tel que f(x) = y
- Comme f est strictement monotone, y ne possède qu'un seul antécédent. En effet, si $f (x 1) = f (x 2)$ , la stricte monotonie de f empêche $x 1$ d'être différent de $x 2$ .

Généralisation. Le théorème se généralise à des intervalles I ouverts ou semi-ouverts, l'intervalle J est alors un intervalle de même nature que I. Le terme de même nature doit être explicité. Le théorème de la bijection précise que

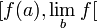
si I=[a, b[ et f est croissante, l'intervalle J est $[f(a), \lim_b f[$
si I=[a, b[ et f est décroissante, l'intervalle J est $]\lim_b f, f(a)]$
etc.

Formulations équivalentes du théorème. si f est continue strictement monotone sur un intervalle I de bornes a et b

pour tout élément $k$ strictement compris entre les limites de f en a et b, il existe un unique $c$ de $I$ tel que $f (c) = k$
pour tout élément $k$ strictement compris entre les limites de f en a et b, l'équation $f (x) = k$ d'inconnue x admet une unique solution dans $I$ .

Remarques

Ce théorème permet de prouver l'existence de fonctions réciproques et de bâtir ainsi une large famille de fonctions élémentaires essentielles à l'élaboration de la branche des mathématiques appelée analyse.

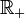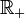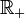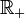Les fonctions définies de $\mathbb{R}_+$ dans $\mathbb{R}_+$ qui à $x\,$ associent $\sqrt[n]{x}\,$ sont les fonctions réciproques des fonctions définies de $\mathbb{R}_+$ dans $\mathbb{R}_+$ qui à $x\,$ associent $x^n\,$ .
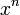les fonctions réciproques des fonctions trigonométriques classiques, arc sinus, arc cosinus et arc tangente, sont aussi définies grâce à ce théorème.

Ce théorème n'est pas vrai sur les nombres rationnels, ce qui a empêché une construction rigoureuse de l'analyse jusqu'au XIX^e siècle. Pour une approche rigoureuse, il a fallu attendre les travaux de Dedekind et de Cauchy qui ont fourni une construction des nombres réels.

Le théorème de la bijection donne des conditions suffisantes pour construire une bijection d'un intervalle I sur un intervalle J mais ces conditions ne sont pas nécessaires. Il existe en effet des bijections de I sur J qui ne sont ni continues ni monotones. En revanche,

une fonction continue sur I qui ne serait pas monotone ne peut pas être une bijection de I sur f(I).
une fonction monotone sur un intervalle I non continue ne peut pas déterminer une bijection de l'intervalle I sur un intervalle J.

Démonstrations de ces résultats

La fonction f définie sur [0;2] par f(x)=x si x appartient à [0;1[ et f(x)=3 - x si x appartient [1;2] définit une bijection de [0;2] sur [0;2] alors qu'elle n'est ni monotone ni continue.
Si une fonction n'est pas monotone sur I, il existe trois réels a <b< c pour lesquels f(b) n'est pas entre f(a) et f(c). Soit k la valeur prise parmi f(a) et f(c), la plus proche de f(b). Cette valeur k est comprise entre f(b) et f(a), la fonction f étant continue, d'après le théorème des valeurs intermédiaires, la valeur k possède un antécédent dans l'intervalle [a, b[ . De même, k étant compris entre f(b) et f(c), k possède un antécédent dans l'intervalle [b, c[. La fonction ne peut donc pas être bijective.
Si f est une fonction monotone, par exemple croissante sur un intervalle I, elle possède en tout point intérieur à son ensemble de définition, une limite à droite et une limite à gauche. Si f n'est pas continue en c alors 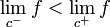$\lim_{c^-}f < \lim_{c^+}f$ . Or, pour tout x < c, 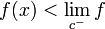$f(x) < \lim_{c^-}f$ et, pour tout x > c, 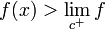$f(x) >\lim_{c^+}f$ . L'ensemble f(I) comporte donc un trou : $[\lim_{c^-}f ,\lim_{c^+}f ]-\{f(c)\}$ et ne peut donc pas être un intervalle. (Si la non continuité est à une des bornes, on remplace une des limites par la valeur en c).

Utilisation pratique

Remarquons que l'application $f$ donnée n'est pas forcément bijective. Dans la pratique, pour appliquer ce théorème, nous devons

vérifier que $f$ est continue sur $I$ ,
vérifier que $f$ est strictement monotone,
déterminer l'intervalle $J = f (I)$ qui est de même type que l'intervalle $I$ (ouvert, fermé ou semi-ouvert), dont les bornes sont les limites de $f$ aux bornes de $I$ , ou les valeurs que prend $f$ aux bornes.

Homéomorphisme

En réalité, les propriétés requises permettent de démontrer non seulement l'existence d'une bijection mais aussi le caractère continu de sa réciproque. Une fonction continue de A vers B dont la réciproque est continue de B vers A est appelée un homéomorphisme. le théorème de la bijection peut alors s'énoncer ainsi :

Théorème de la bijection (version 2) — Soit I un intervalle et f une fonction continue et strictement monotone de I dans 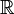$\textstyle \R$ . En notant 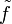$\tilde{f}$ la même fonction restreinte à l'arrivée à $f (I)$ , on a alors

$f (I)$ est un intervalle de $\R$
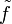$\tilde{f}$ est bijective
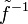$\tilde{f}^{-1}$ est strictement monotone de même sens que $f$
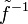$\tilde{f}^{-1}$ est continue sur $f (I)$ .

Démonstration du théorème

f(I) est un intervalle. Ceci est une conséquence directe du théorème des valeurs intermédiaires car I est un intervalle et f est continue sur I
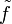$\tilde{f}$ est bijective. La démonstration est analogue à celle faite pour la version (1).
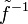$\tilde{f}^{-1}$ est strictement monotone de même sens que $f$ . On suppose 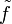$\tilde{f}$ strictement croissante (un raisonnement analogue est possible avec 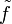$\tilde{f}$ strictement décroissante). Soient $y 1$ < $y 2$ deux éléments de J et $x 1$ et $x 2$ leur antécédent pour f. Les réels $y 1$ et $y 2$ étant distincts, il en est de même de $x 1$ et $x 2$ , de plus $x 1 > x 2$ entrainerait $f (x 1) > f (x 2)$ , c'est-à-dire $y 1 < y 2$ , car f est croissante. Ce n'est pas le cas, donc $x 1 < x 2$ , c'est-à-dire 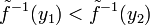$\tilde{f}^{-1}(y_1)<\tilde{f}^{-1}(y_2)$ . On a bien démontré que 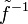$\tilde{f}^{-1}$ était croissante.
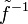$\tilde{f}^{-1}$ est continue. Ceci est une conséquence de la remarque énoncée plus haut : 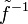$\tilde{f}^{-1}$ est une fonction monotone d'un intervalle J sur un intervalle I. Si 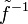$\tilde{f}^{-1}$ n'était pas continue, elle ne pourrait pas définir une bijection de J sur I. Donc 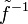$\tilde{f}^{-1}$ est continue

Le fait qu'une bijection continue ait une réciproque continue n'est pas une évidence.

Cette propriété peut être fausse si l'ensemble de départ ou d'arrivée n'est pas $\R$ .
Cette propriété peut être fausse si l'ensemble de départ n'est pas un intervalle de $\R$
Cette propriété est une propriété globale: un bijection de $\R$ dans $\R$ , continue en a peut avoir une réciproque non continue en f(a).

Contre-exemples

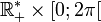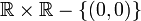La fonction de $\R_+^*\times [0;2\pi[$ dans $\R \times \R - \{(0,0)\}$ qui a $(r,θ)$ associe $(r cos(θ), r sin(θ))$ est une bijection continue dont la réciproque n'est pas continue en (1,0)
La fonction de 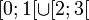$[0;1[ \cup [2;3[$ dans [0;2[ qui, au réel x, associe x si x < 1 et x -1 si x ≥ 2 est une bijection continue strictement monotone dont la réciproque n'est pas continue en 1.
Bertrand Hauchecorne^[1] montre que la fonction de dans , impaire, définie par
- f(2k)=k pour tout entier naturel k
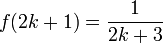- $f(2k+1) = \frac{1}{2k+3}$ pour tout entier naturel k
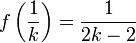- $f\left(\frac 1k\right)=\frac 1{2k-2}$ pour tout entier k strictement plus grand que 1
- f(x) = x pour tout réel différent d'un entier ou de l'inverse d'un entier

est une bijection continue en 0 dont la réciproque n'est pas continue en 0

Notes et références

↑ Bertrand Hauchecorne, Les contre-exemples en mathématiques, Ellipses, ISBN 2-7298-8806-3, p 61

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me de la bijection ».

Catégories : Analyse réelle | Théorème de mathématiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de la bijection de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Théorème de la bijection — En analyse réelle, le théorème de la bijection est un corollaire du théorème des valeurs intermédiaires, affirmant qu une fonction continue et strictement monotone sur un intervalle constitue une bijection entre cet intervalle et son image. Cette … Wikipédia en Français
Theoreme des valeurs intermediaires — Théorème des valeurs intermédiaires Pour les articles homonymes, voir TVI. Le théorème des valeurs intermédiaires (TVI) est un théorème important en analyse et concerne des fonctions continues sur un intervalle. Il indique que si une fonction… … Wikipédia en Français
Théorème de Bolzano — Théorème des valeurs intermédiaires Pour les articles homonymes, voir TVI. Le théorème des valeurs intermédiaires (TVI) est un théorème important en analyse et concerne des fonctions continues sur un intervalle. Il indique que si une fonction… … Wikipédia en Français
Bijection réciproque — Pour les articles homonymes, voir Réciproque (homonymie). En mathématiques, la bijection réciproque d une bijection f est l application qui associe à chaque élément de l ensemble d arrivée son unique antécédent par f. On l appelle parfois, par… … Wikipédia en Français
Théorème d'inversion locale — En mathématiques, le théorème d inversion locale est un résultat de géométrie différentielle. Il indique que si une fonction f est continûment différentiable en un point, si sa différentielle en ce point est une bijection bicontinue, c est à dire … Wikipédia en Français
Bijection — En mathématiques, une bijection est une application bijective. Une application est bijective si et seulement si tout élément de son ensemble d arrivée a un et un seul antécédent, c est à dire est image d exactement un élément de son ensemble de… … Wikipédia en Français
Théorème des valeurs intermédiaires — Pour les articles homonymes, voir TVI. Le théorème des valeurs intermédiaires (TVI) est un théorème important en analyse et concerne des fonctions continues sur un intervalle. Il indique que si une fonction continue sur un intervalle prend deux… … Wikipédia en Français
Theoreme de Cantor-Bernstein — Théorème de Cantor Bernstein Le théorème de Cantor Bernstein, également appelé théorème de Cantor Schröder Bernstein, est un théorème de la théorie des ensembles. Il est nommé en l honneur des mathématiciens Georg Cantor, Felix Bernstein et Ernst … Wikipédia en Français
Théorème de Cantor-Schröder-Bernstein — Théorème de Cantor Bernstein Le théorème de Cantor Bernstein, également appelé théorème de Cantor Schröder Bernstein, est un théorème de la théorie des ensembles. Il est nommé en l honneur des mathématiciens Georg Cantor, Felix Bernstein et Ernst … Wikipédia en Français
Théorème de Schröder-Bernstein — Théorème de Cantor Bernstein Le théorème de Cantor Bernstein, également appelé théorème de Cantor Schröder Bernstein, est un théorème de la théorie des ensembles. Il est nommé en l honneur des mathématiciens Georg Cantor, Felix Bernstein et Ernst … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Theoreme de la bijection

Théorème de la bijection

Sommaire