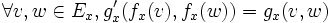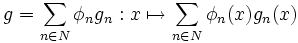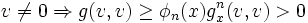Métrique Riemannienne

Métrique riemannienne

Les métriques riemanniennes sont les objets d'étude de la géométrie riemannienne. La première introduction a été donnée par Riemann en 1854. Cependant, son article sur le sujet a été publié après sa mort, en 1868. La même année, Helmholtz publie des résultats analogues.

Les métriques riemanniennes sont des collections différentiables de formes quadratiques définies positives :

Sur un fibré vectoriel 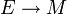$E\rightarrow M$ , une métrique riemannienne $g = g x$ est la donnée d'un produit scalaire $g x$ sur la fibre $E x$ qui dépende de manière lisse du point de base 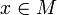$x\in M$ . Plus formellement, 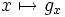$x\mapsto g_x$ est une section en tout point définie positive du fibré vectoriel des formes bilinéaires symétriques 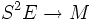$S^2E\rightarrow M$ . On dit que la donnée $(E, g)$ est un fibré riemannien.

Pour deux fibrés riemanniens

(E, g)

(F, g')

, un morphisme de fibrés riemanniens 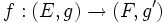$f:(E,g)\rightarrow (F,g')$ est un morphisme de fibré 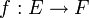$f:E\rightarrow F$ tel que, pour tout 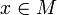$x\in M$ , l'application linéaire 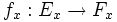$f_x:E_x\rightarrow F_x$ est une isométrie linéaire, id est :

$\forall v,w\in E_x, g'_x(f_x(v),f_x(w))=g_x(v,w)$

Si $M$ est une variété différentielle (de dimension n), une métrique riemannienne sur $M$ est simplement une métrique riemannienne $g$ sur le fibré tangent 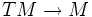$TM\rightarrow M$ . La donnée $(M, g)$ est une variété riemannienne.

Etant données deux variétés riemanniennes

(M, g)

(N, g')

, une isométrie 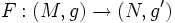$F:(M,g)\rightarrow (N,g')$ est une application différentiable 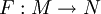$F:M\rightarrow N$ telle que l'application tangente 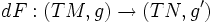$dF:(TM,g)\rightarrow (TN,g')$ est un morphisme de fibrés riemanniens. Cette derniere condition se reecrit :

F * g = g

Exemples

Tout produit scalaire $< , >$ sur $R n$ induit sur tout fibré vectoriel trivial 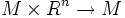$M\times R^n\rightarrow M$ une métrique riemannienne :

g x ((x, v),(x, w)) = < x, w >

Soit $g$ une métrique riemannienne sur 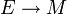$E\rightarrow M$ . Pour une fonction différentiable 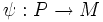$\psi:P\rightarrow M$ , il existe sur le fibré vectoriel tiré en arrière 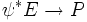$\psi^*E\rightarrow P$ une unique métrique riemannienne $ψ * g$ telle que le morphisme naturel 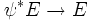$\psi^*E\rightarrow E$ soit un isomorphisme de fibrés riemanniens.

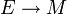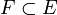Si $g$ est une métrique riemannienne sur $E\rightarrow M$ , alors, par restriction, $g$ définit une métrique riemannienne sur tout sous-fibré vectoriel $F\subset E$ .

Existence

Sur tout fibré vectoriel 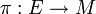$\pi:E\rightarrow M$ , il existe une métrique riemannienne.

Démonstrations

Preuve via une partition de l'unité.

Pour tout ouvert U suffisamment petit de M, le fibré vectoriel 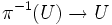$\pi^{-1}(U)\rightarrow U$ est trivialisable. Or, par ci-dessus, tout fibré vectoriel trivialisable admet une métrique riemannienne. Donc, il existe une métrique riemannienne $g U$ sur $π - 1 (U)$ .

En utilisant la paracompacité de $M$ , il existe un recouvrement (strictement) dénombrable 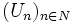$(U_n)_{n\in N}$ de $M$ tel que, pour tout 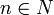$n\in N$ , il existe une métrique riemannienne $g n$ sur le fibré vectoriel 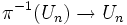$\pi^{-1}(U_n)\rightarrow U_n$ . Soit 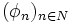$(\phi_n)_{n\in N}$ une partition de l'unité subordonnée à 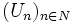$(U_n)_{n\in N}$ . L'application 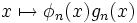$x\mapsto \phi_n(x)g_n(x)$ est une section globale de 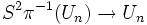$S^2\pi^{-1}(U_n)\rightarrow U_n$ nulle au voisinage de la frontière 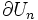$\partial U_n$ . 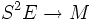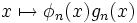Elle se prolonge par $0$ en une section globale de $S^2E\rightarrow M$ , abusivement notée $x\mapsto \phi_n(x)g_n(x)$ .

On pose alors :

$g=\sum_{n\in N} \phi_ng_n:x\mapsto \sum_{n\in N}\phi_n(x)g_n(x)$

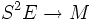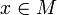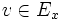C'est une section de $S^2E\rightarrow M$ , et elle bien définie positive en tout point : si $x\in M$ appartient à l'intérieur du support de $φ n$ , et pour tout vecteur $v\in E_x$ ,

$v\neq 0\Rightarrow g(v,v)\geq \phi_n(x)g^n_x(v,v)>0$

Preuve via un plongement.

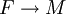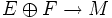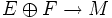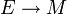Il existe un fibré vectoriel $F\rightarrow M$ tel que $E\oplus F\rightarrow M$ soit trivialisable. On utilise à ce niveau la paracompacité de $M$ . Il existe donc une métrique riemannienne sur $E\oplus F\rightarrow M$ qui se restreint en une métrique riemannienne sur $E\rightarrow M$ .

Attention : bien que plus court en apparence, ce second argument dissimule la difficulté dans l'existence de $F$ . Cette existence fait aussi appel à un argument de partition de l'unité (!!!).

Sur toute variété différentielle $M$ , il existe une métrique riemannienne.

Voir aussi

Portail de la géométrie

Ce document provient de « M%C3%A9trique riemannienne ».

Catégories : Géométrie riemannienne | Algèbre bilinéaire

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Métrique Riemannienne de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Metrique riemannienne — Métrique riemannienne Les métriques riemanniennes sont les objets d étude de la géométrie riemannienne. La première introduction a été donnée par Riemann en 1854. Cependant, son article sur le sujet a été publié après sa mort, en 1868. La même… … Wikipédia en Français
Métrique riemannienne — En géométrie différentielle, les métriques riemanniennes sont la notion de base de la géométrie riemannienne. La première introduction a été donnée par Riemann en 1854. Cependant, son article sur le sujet a été publié après sa mort, en 1868. La… … Wikipédia en Français
Métrique pseudo-riemannienne — En mathématiques et en physique, une métrique pseudo riemannienne est une extension de la métrique riemannienne dans laquelle un certain nombre d axes de l espace qu elle décrit ont des normes négatives. Si la métrique pseudo riemanienne est en… … Wikipédia en Français
Métrique de Carnot-Carathéodory — En géométrie différentielle, on appelle métrique de Carnot Carathéodory (d après le physicien français Sadi Carnot et le mathématicien grec Constantin Carathéodory) une forme bilinéaire (principalement définie positive) définie sur une… … Wikipédia en Français
Metrique (mathematiques) — Métrique (mathématiques) Pour les articles homonymes, voir Métrique. En mathématiques, une métrique ou fonction distance est une fonction qui définit une distance entre les éléments d un ensemble. Un ensemble avec une métrique est appelé un… … Wikipédia en Français
Métrique (mathématiques) — Pour les articles homonymes, voir Métrique. En mathématiques, une métrique ou distance est une fonction qui définit la distance entre les éléments d un ensemble. Un ensemble muni d une distance est appelé un espace métrique. Toute distance induit … Wikipédia en Français
Métrique de Poincaré — En mathématiques, et plus précisément en géométrie différentielle, la métrique de Poincaré, due à Henri Poincaré, est le tenseur métrique décrivant une surface de courbure négative constante. C est la métrique naturelle utilisée pour des calculs… … Wikipédia en Français
Lexique de la géométrie riemannienne — La géométrie riemannienne est un domaine des mathématiques étudiant les propriétés des variétés riemanniennes. Cette page rappelle brièvement les définitions des termes récurrents rencontrés. Sommaire : Haut A B C D E F G H I J K L M N O P Q … Wikipédia en Français
Variété riemannienne — En mathématiques, et plus précisément en géométrie, une variété riemannienne est une variété différentielle ayant une structure supplémentaire (une métrique riemannienne) permettant de définir la longueur d un chemin entre deux points de la… … Wikipédia en Français
Variete riemannienne — Variété riemannienne Une variété riemannienne est une variété différentielle ayant une structure supplémentaire permettant de définir la longueur d un chemin entre deux points de la variété. Sommaire 1 Définitions et exemples élémentaires 1.1… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Métrique Riemannienne