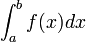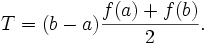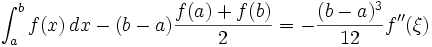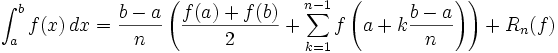Méthode Des Trapèzes

Méthode des trapèzes

Principe de la méthode : l'aire sous la courbe représentative de f est approchée par l'aire sous une droite affine (en rouge)

En analyse numérique, la méthode des trapèzes est une méthode permettant de réaliser le calcul numérique d'une intégrale

$\int_{a}^{b} f(x)dx$

Sommaire

1 Intervalle unique
2 Intervalles multiples
3 Exemple d'approximation d'une fonction par des trapèzes
4 Divers théorèmes
5 Lien avec les autres méthodes d'intégration
6 Notes et références
7 Voir aussi

Intervalle unique

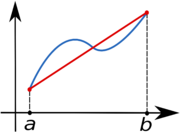
Le principe est d'approcher la région sous la courbe représentative de la fonction $f$ par un trapèze et d'en calculer l'aire :

$T=(b-a)\frac{f(a) + f(b)}{2}.$

Pour une fonction à valeurs réelles, deux fois continûment différentiable sur le segment $[a, b]$ , l'erreur ^[1] est de la forme

$\int_a^b f(x)\,dx -(b-a)\frac{f(a) + f(b)}{2} = -\frac{(b-a)^3}{12}f''(\xi)$

pour un certain $\xi \in [a,b]\,$ .

Notamment, dans le cas d'une fonction convexe, l'aire du trapèze est une valeur approchée par excès de l'intégrale.

Intervalles multiples

Pour obtenir de meilleurs résultats, on découpe l'intervalle $[a, b]$ en n intervalles plus petits et on applique la méthode sur chacun d'entre eux :

$\int_a^b f(x)\,dx = \frac{b-a}{n} \left( {f(a) + f(b) \over 2} + \sum_{k=1}^{n-1} f \left( a+k \frac{b-a}{n} \right) \right) + R_n(f)$

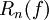$R_n(f)\,$ est l'erreur de quadrature ^[1] et vaut: 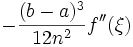$-\frac{(b-a)^3}{12n^2}f''(\xi)$ pour un $\xi \in [a,b]\,$

La méthode des trapèzes consiste donc à remplacer la fonction par une fonction continue et affine par morceaux (opération d'interpolation linéaire) et à considérer l'aire de cette dernière comme valeur approchée de l'aire de la fonction initiale.

Exemple d'approximation d'une fonction par des trapèzes

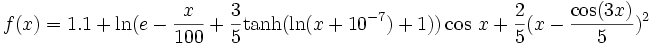
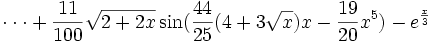
Voici le découpage d'une fonction f que l'on veut intégrer sur l'intervalle $[0;2]$ $f(x)=1.1 + \ln(e-\frac{x}{100}+\frac{3}{5}\operatorname{tanh}(\ln(x+10^{-7})+1))\cos \,x + \frac{2}{5}(x-\frac{\cos(3x)}{5})^2 \,\!$ $\cdot \cdot \cdot + \frac{11}{100} \sqrt{2+2x} \sin (\frac{44}{25}(4+3\sqrt{x})x-\frac{19}{20}x^5)-e^{\frac{x}{3}} \,\!$

Découpage pour différentes valeurs de n (2,8 et 16).

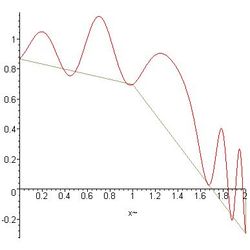
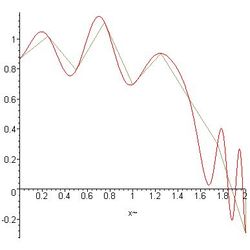
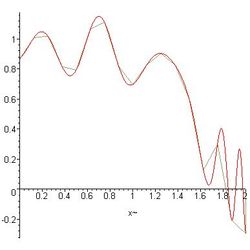
Divers théorèmes

Théorème : Si f est 2 fois continûment différentiable sur $[a, b]$ , la méthode des trapèzes est convergente sur $C 2 ([a, b])$ .
Théorème : La méthode des trapèzes est stable.

Lien avec les autres méthodes d'intégration

La méthode des trapèzes est une application des formules de Newton-Cotes, la méthode de Simpson en est une autre, plus précise.

La méthode de Romberg est un procédé d'accélération de la convergence de la méthode des trapèzes.

Notes et références

↑ ^{a et b} En métrologie, l'erreur est définie comme la différence Valeur approchée - Valeur réelle soit l'opposé de l'erreur définie dans cet article, qui, en métrologie, porte le nom de correction (Aimé Defix, Éléments de métrologie générale et de métrologie légale, p 72-74)

Voir aussi

Calcul intégral (mathématiques élémentaires)
Formule d'Euler-Maclaurin
Formules de Newton-Cotessur Math-Linux.com

Ce document provient de « M%C3%A9thode des trap%C3%A8zes ».

Catégorie : Intégration numérique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Méthode Des Trapèzes de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Methode des trapezes — Méthode des trapèzes Principe de la méthode : l aire sous la courbe représentative de f est approchée par l aire sous une droite affine (en rouge) En analyse numérique, la méthode des trapèzes est une méthode permettant de réaliser le calcul … Wikipédia en Français
Méthode des trapèzes — Principe de la méthode : l aire sous la courbe représentative de f est approchée par l aire sous une droite affine (en rouge) En analyse numérique, la méthode des trapèzes est une méthode permettant de réaliser le calcul numérique d une… … Wikipédia en Français
Methode de Romberg — Méthode de Romberg En analyse numérique, la méthode d intégration de Romberg est une méthode récursive de calcul numérique d intégrale, basée sur l application du procédé d extrapolation de Richardson à la méthode des trapèzes. Cette technique d… … Wikipédia en Français
Méthode De Romberg — En analyse numérique, la méthode d intégration de Romberg est une méthode récursive de calcul numérique d intégrale, basée sur l application du procédé d extrapolation de Richardson à la méthode des trapèzes. Cette technique d accélération permet … Wikipédia en Français
Méthode de romberg — En analyse numérique, la méthode d intégration de Romberg est une méthode récursive de calcul numérique d intégrale, basée sur l application du procédé d extrapolation de Richardson à la méthode des trapèzes. Cette technique d accélération permet … Wikipédia en Français
Methode de Crank-Nicolson — Méthode de Crank Nicolson Simulation de l expérience des fentes de Young pour un électron, avec la méthode de Crank Nicolson. En mathématiques, en analyse numérique, la méthode de Crank Nicolson est un algorithme simple permettant de résoudre des … Wikipédia en Français
Méthode De Crank-Nicolson — Simulation de l expérience des fentes de Young pour un électron, avec la méthode de Crank Nicolson. En mathématiques, en analyse numérique, la méthode de Crank Nicolson est un algorithme simple permettant de résoudre des systèmes d équations aux… … Wikipédia en Français
Méthode de crank-nicolson — Simulation de l expérience des fentes de Young pour un électron, avec la méthode de Crank Nicolson. En mathématiques, en analyse numérique, la méthode de Crank Nicolson est un algorithme simple permettant de résoudre des systèmes d équations aux… … Wikipédia en Français
Méthode de Romberg — En analyse numérique, la méthode d intégration de Romberg est une méthode récursive de calcul numérique d intégrale, basée sur l application du procédé d extrapolation de Richardson à la méthode des trapèzes. Cette technique d accélération permet … Wikipédia en Français
Trapèzes — Trapèze Pour les articles homonymes, voir Trapèze (homonymie) … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Méthode Des Trapèzes