- Méthode Des Différences Finies
-
Méthode des différences finies
Dans le domaine de l'analyse numérique, on peut être amené à rechercher la solution d'une équation aux dérivées partielles. Parmi les méthodes de résolutions couramment pratiquées, la méthode des différences finies est la plus facile d'accès, puisqu'elle repose sur deux notions : la discrétisation des opérateurs de dérivation/différentiation (assez intuitive) d'une part, et la convergence du schéma numérique ainsi obtenu d'autre part.
Sommaire
Approximation des opérateurs par formules de Taylor
Grâce aux formules de Taylor, on définit la discrétisation des opérateurs différentiels (dérivées premières, secondes, etc, partielles ou non).
La formulation de Taylor-Young est préférable dans son utilisation simple, la formulation de Taylor avec reste intégral de Laplace permet de mesurer les erreurs (cf. plus bas)
Exemple d'approximation d'opérateur
Par exemple, écrivons en un point x et pour une valeur h telle que u est dérivable trois fois sur un intervalle contenant strictement [x − h,x + h], on sait écrire les deux formules de Taylor-Young :
et :
où toutes les applications
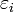 convergent vers 0 avec h. Alors :
convergent vers 0 avec h. Alors :et en sommant les développements pour x-h et x+h l'on obtient:
on obtient respectivement des approximations de 1er ordre et 2nd ordre en h.
Maillage
Un maillage est un ensemble de points du domaine de définition sur lequel on va appliquer la méthode des différences finies. Pour une application définie sur un segment de
 , on ajoutera en général les deux extrémités du segment ; pour un maillage en dimension supérieure, on sera amené à choisir, éventuellement, des points du contours du domaine de définition.
, on ajoutera en général les deux extrémités du segment ; pour un maillage en dimension supérieure, on sera amené à choisir, éventuellement, des points du contours du domaine de définition.On appelle le pas du maillage la distance entre deux points successifs du maillage voisins. En dimension 1, cela se simplifie en différence des abscisses. Ce pas n'est pas nécessairement constant, il peut même être judicieux de ne pas le fixer comme tel. Le pas (global) de l'approximation peut être défini comme le plus grand pas du maillage. Ainsi, si ce pas global tend vers 0, cela veut dire que la répartition des points du maillage dans l'intervalle choisi tend à se faire sur tout le domaine d'étude par densité.
Exemple de maillage
Pour un intervalle de validité [0,1] on utilisera (M + 1) points, par exemple {0,h,2h,...,Mh = 1} pour un pas constant
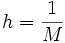 .
.Degré de dérivation
Pour des raisons à la fois d'écriture algébrique et d'étude de convergence/stabilité a priori il est important de se replacer autant que possible dans une problématique avec des ordres de dérivation les plus faibles possible, quitte à augmenter la dimension de l'espace d'étude. On fera ainsi appel à des variables intermédiaires : les dérivées ou dérivées partielles des fonctions initialement étudiées.
Exemple d'abaissement de degré de dérivation
- u''(x) + ω2u(x) = 0,u(0) = u0,u'(0) = u1
s'écrira volontiers avec le choix :
ce qui donnera l'équation pour U :
Avec
Donc le degré de dérivation est ici réduit à 1, alors que la dimension de l'espace d'arrivée est devenue 2.
Schéma numérique
Écrire un schéma numérique de résolution de l'équation différentielle initiale signifie :
- substituer les formulations des dérivées/différentielles obtenues par approximation aux opérateurs eux-mêmes sur tous les points du maillage.
- réorganiser les équations pour faire apparaître un schéma explicite (ex : les valeurs à la date t+1 données en fonction des valeurs des dates 0 à t) ou implicite (une équation lie les valeurs passées, présentes et futures sans qu'on arrive à exprimer ces dernières seules).
Dans un cadre de modélisation classique d'opérateurs linéaires dans des équations différentielles linéaires, on aboutit à un système d'équations linéaires de dimension égale au nombre de nœuds du maillage (en fait un peu moins, du fait des données initiales, par exemple).
Résoudre le schéma numérique signifie simplement trouver les valeurs discrètes de la fonction en chaque nœud.
Un système issu d'une équation linéaire peut souvent être algébriquement simple à résoudre. Pour simplifier, on peut dire que les schémas explicites engendrent des systèmes d'équation à matrice triangulaire ou trigonalisables, ce qui n'est pas le cas des schémas implicites.
Les méthodes de résolution des schémas peuvent faire appel à des méthodes d'optimisation comme à des méthodes algébriques classiques.
Exemple de schéma numérique
Partons de l'équation suivante :
![\forall x \in [0, 1], u'( x ) - \tau u( x ) = 0, u( 0 ) = u_0](/pictures/frwiki/50/2400bbacfdd289f513a4cfda2846e86f.png)
Alors, on choisit d'écrire le schéma d'ordre 1 de la dérivée première en tous les points d'un maillage à pas constant {x0 = 0,x1 = h,x2 = 2h,...,xM = Mh = 1}. On recherche exactement M inconnues, les valeurs qu'on écrira
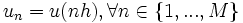 . Le schéma est alors appelé schéma d'Euler explicite d'ordre 1 :
. Le schéma est alors appelé schéma d'Euler explicite d'ordre 1 :Ce qui donne explicitement la relation de récurrence entre un et son successeur un + 1
Soit une suite géométrique qui nous donne assez facilement, en remplaçant h par sa valeur
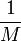 :
:On dispose donc pour tous les points du maillage de la valeur de la solution du problème selon la méthode des différences finies. Pour les points non contenus sur le maillage, il faudra alors faire une hypothèse sur la qualité de la solution, par exemple supposer que la fonction est constante ou affine par morceaux.
Choisissons plutôt de partir du schéma d'ordre 2 de la dérivée première, sauf pour le point n = 1 pour lequel on reprend le schéma d'ordre 1 :
Ceci nous donne alors
où la matrice A est tridiagonale, avec des − 2τh sur la diagonale, des 1 sur la 1ère surdiagonale et des -1 sur la 1ère sousdiagonale.
Convergences
La deuxième notion complète la première. Elle traite de la convergence d'un schéma numérique. En effet, une modélisation par différences finies est un couple (conditions (initiales, finales, etc), schéma numérique) dont on ne sait a priori pas si son éventuelle solution est proche ou non d'une solution réelle espérée du système initial (conditions (initiales, finales, etc), équations différentielles). Pour parler de convergence, il est nécessaire de comprendre celle-là selon un critère similaire à ceux-ci, si on étudie une fonction f sur un intervalle [a,b] :
- convergence simple : en n'importe quel point l'approximation évaluée tend vers la vraie valeur de la solution quand le pas tend vers 0
- convergence en norme 2
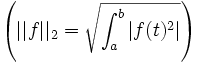 : cette norme tend vers 0 avec le pas
: cette norme tend vers 0 avec le pas- convergence absolue ou en norme absolue
![\left( ||f||_\infty = \max_{ t \in [a,b] }{|f(t)|} \right)](/pictures/frwiki/48/0c39ec6226ec0a8041a3a00e25f51d89.png) : cette norme tend vers 0 avec le pas
: cette norme tend vers 0 avec le pasOn doit alors étudier la qualité de la convergence de ce schéma numérique selon des critères tels que la stabilité, la robustesse et bien-sûr différentes normes (2 ou
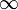 la plupart du temps). Cela peut aussi bien dépendre de la méthode de discrétisation, de la nature des équations que des conditions initiales (selon la nature du problème posé).
la plupart du temps). Cela peut aussi bien dépendre de la méthode de discrétisation, de la nature des équations que des conditions initiales (selon la nature du problème posé).- La stabilité, la robustesse du schéma : [à rajouter]
Exemple d'erreur d'approximation
Pour un maillage donné, l'erreur entre la solution approchée et la solution réelle est déterminée par l'erreur de troncature, comme définie notamment dans le théorème de Taylor avec reste intégral ou au sens de la restriction à une partie finie d'une série de Taylor qui possède un nombre infini de termes.
Là encore, l'erreur dépend de ce qu'on entend mesurer. L'erreur peut en effet être mesurée point par point (convergence simple) ou selon une norme 2 ou infinie.
Dans le dernier exemple présenté, on connaît la solution exacte de l'équation, qui est une fonction exponentielle.
- u(x) = u0e(τx)
On sait donc évaluer la différence directement entre la version réelle et la version estimée par approximation pour un maillage M intervalles :
Ici, on a une mesure exacte de l'erreur point par point. Notons qu'on peut aussi démontrer que si le maillage s'affine infiniment (c'est-à-dire que le nombre de points M tend vers l'infini), alors la convergence simple est assurée. Prenons un exemple : le point
 . Distinguons le cas M pair. Le cas où M est impair est identique par encadrement, même s'il est un peu plus compliqué.
. Distinguons le cas M pair. Le cas où M est impair est identique par encadrement, même s'il est un peu plus compliqué.Si M est pair, alors le point
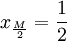 . La différence d'image est alors
. La différence d'image est alorsOr, un résultat classique d'analyse nous donne la limite de la suite
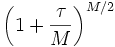 est
est 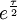 , ce qui fait que la différence
, ce qui fait que la différence 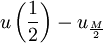 tend bien vers 0.
tend bien vers 0.Il est en fait possible, en utilisant le caractère archimédien et la continuité des solutions, de montrer que la convergence simple est assurée partout...
Voir aussi
Articles connexes
- Consistance d'un schéma numérique
- Méthode des éléments finis
- Méthode des volumes finis
- Théorème de Lax
- Théorème de Lax-Wendroff
Liens et documents externes
- (fr) Liens vers des outils de discrétisation (téléchargeables)
- (fr) Formulations mathématiques et résolution numérique en mécanique
- Portail des mathématiques
Catégorie : Équations différentielles numériques
Wikimedia Foundation. 2010.

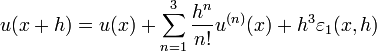
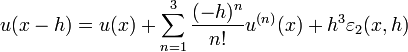
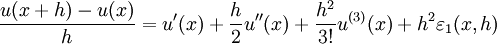
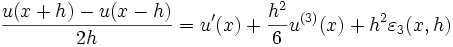
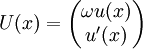
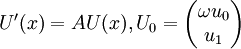

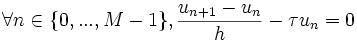
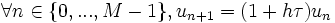
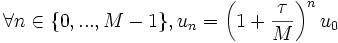
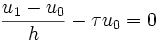
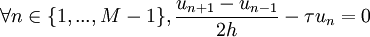
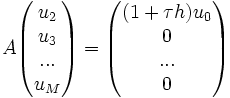
![\forall n \in \{ 0, ..., M \}, u( x_n ) - u_n = u_0 \left[ e^{ \frac{ \tau n }{M}} - \left( 1 + \frac{ \tau }{ M } \right)^n \right]](/pictures/frwiki/51/37f65c3d1c1b4e0838528cdfd2159924.png)
![u\left( \frac{1}{2} \right) - u_{ \frac{M}{2} }= u_0 \left[ e^{ \frac{ \tau }{2}} - \left( 1 + \frac{ \tau }{ M } \right)^{ M / 2 } \right]](/pictures/frwiki/101/e8aa13087f1e8440f2a8cdf36152f5c1.png)