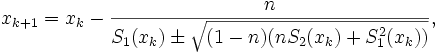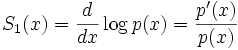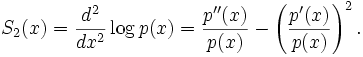Méthode De Laguerre

Méthode de Laguerre

En analyse numérique, la méthode de Laguerre est un algorithme de recherche d'un zéro d'une fonction polynomiale. En d'autres termes, la méthode de Laguerre peut être utilisée pour trouver une valeur approchée d'un solution d'une équation de la forme

p(x) = 0

où p est un polynôme donné.

Principe

Soit p un polynôme. Soit x₀ un réel supposé être une valeur approchée d'une racine de p. La méthode de Laguerre tente d'améliorer cette première approximation par une méthode itérative en utilisant la relation récurrente:

$x_{k+1} = x_k - \frac{n}{S_1(x_k) \pm \sqrt{(1-n)(nS_2(x_k)+S_1^2(x_k))}},$

dans laquelle le symbole ± au dénominateur est remplacé par + ou − selon ce qui donne un dénominateur ayant le plus grand module possible. De plus, n désigne le degré du polynôme p, S₁ et S₂ sont les premières et secondes dérivées logarithmiques de p, données par

$S_1(x) = \frac{d}{dx} \log p(x) = \frac{p'(x)}{p(x)}$

$S_2(x) = \frac{d^2}{dx^2} \log p(x) = \frac{p''(x)}{p(x)} - \left( \frac{p'(x)}{p(x)} \right)^2.$

Propriétés

Si x est une racine simple du polynôme p, alors la méthode de Laguerre aura une vitesse de convergence cubique lorsque la valeur approchée initiale x₀ sera assez proche de la racine x. Cependant, si x est une racine multiple, alors la convergence sera seulement linéaire.

Cela signifie que la méthode de Laguerre converge encore plus rapidement que la méthode de Newton. Cependant, la méthode de Laguerre exige le calcul des dérivées premières et secondes de p, alors que la méthode de Newton ne demande qu'une dérivée.

La méthode de Laguerre fonctionne également pour des polynômes à coefficients réels qui ont des racines complexes. Même si la valeur approchée initiale est réelle, alors la méthode fournira des valeurs approchées complexes quand l'expression sous la racine deviendra négative. C'est la grande différence avec la méthode de Newton, qui donnera toujours des solutions réelles dans ce cas.

Références

(en) S. Goedecker, Remark on Algorithms to Find Roots of Polynomials, SIAM J. Sci. Comput. 15(5), 1059–1063 (September 1994).
(en) Wankere R. Mekwi (2001). Iterative Methods for Roots of Polynomials. Master's thesis, University of Oxford.
(en) V. Y. Pan, Solving a Polynomial Equation: Some History and Recent Progress, SIAM Rev. 39(2), 187–220 (June 1997).

Méthodes de résolution d'équations
Résolution d'équations polynomiales	Méthode de Bézout · Méthode de Cardan · Méthode de Sotta · Méthode de Ferrari · Méthode de Descartes · Méthode de Tschirnhaus · Méthode d'Hermite
Recherche d'un zéro	Méthode de dichotomie · Méthode de Newton · Méthode de la sécante · Méthode de Müller · Méthode de Brent · Méthode de la fausse position · Méthode de Héron · Méthode de Laguerre · Méthode du cercle de séparation · Méthode de Halley · Méthode de Householder . Méthode de Quasi-Newton

Portail des mathématiques

Ce document provient de « M%C3%A9thode de Laguerre ».

Catégorie : Algorithme de recherche d'un zéro d'une fonction

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Méthode De Laguerre de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Methode de Laguerre — Méthode de Laguerre En analyse numérique, la méthode de Laguerre est un algorithme de recherche d un zéro d une fonction polynomiale. En d autres termes, la méthode de Laguerre peut être utilisée pour trouver une valeur approchée d un solution d… … Wikipédia en Français
Méthode de laguerre — En analyse numérique, la méthode de Laguerre est un algorithme de recherche d un zéro d une fonction polynomiale. En d autres termes, la méthode de Laguerre peut être utilisée pour trouver une valeur approchée d un solution d une équation de la… … Wikipédia en Français
Méthode de Laguerre — En analyse numérique, la méthode de Laguerre est un algorithme de recherche d un zéro d une fonction polynomiale. En d autres termes, elle peut être utilisée pour trouver une valeur approchée d un solution d une équation de la forme p(x) = 0, où… … Wikipédia en Français
Methode de Newton — Méthode de Newton Isaac Newton En analyse numérique, la méthode de Newton, ou méthode de Newton Raphson[1], est un algorithme efficace pour trouver des approximations d un zéro … Wikipédia en Français
Methode de Sotta — Méthode de Sotta La méthode de Sotta, imaginée et mise au point par Bernard Sotta, permet de résoudre toutes les équations du troisième degré et peut se généraliser à certaines équations de degré supérieur ou égal à 4 si les coefficients de ces… … Wikipédia en Français
Methode de la corde — Méthode de Newton Isaac Newton En analyse numérique, la méthode de Newton, ou méthode de Newton Raphson[1], est un algorithme efficace pour trouver des approximations d un zéro … Wikipédia en Français
Méthode De Newton — Isaac Newton En analyse numérique, la méthode de Newton, ou méthode de Newton Raphson[1], est un algorithme efficace pour trouver des approximations d un zéro … Wikipédia en Français
Méthode De Sotta — La méthode de Sotta, imaginée et mise au point par Bernard Sotta, permet de résoudre toutes les équations du troisième degré et peut se généraliser à certaines équations de degré supérieur ou égal à 4 si les coefficients de ces équations… … Wikipédia en Français
Méthode de Newton-Raphson — Méthode de Newton Isaac Newton En analyse numérique, la méthode de Newton, ou méthode de Newton Raphson[1], est un algorithme efficace pour trouver des approximations d un zéro … Wikipédia en Français
Méthode de la corde — Méthode de Newton Isaac Newton En analyse numérique, la méthode de Newton, ou méthode de Newton Raphson[1], est un algorithme efficace pour trouver des approximations d un zéro … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Méthode De Laguerre