- Métaheuristiques
-
Métaheuristique
Les métaheuristiques forment une famille d’algorithmes d’optimisation visant à résoudre des problèmes d’optimisation difficile (souvent issus des domaines de la recherche opérationnelle, de l'ingénierie ou de l'intelligence artificielle) pour lesquels on ne connaît pas de méthode classique plus efficace.
Les métaheuristiques sont généralement des algorithmes stochastiques itératifs, qui progressent vers un optimum global, c'est-à-dire l'extremum global d'une fonction, par échantillonnage d’une fonction objectif. Elles se comportent comme des algorithmes de recherche, tentant d’apprendre les caractéristiques d’un problème afin d’en trouver une approximation de la meilleure solution (d'une manière proche des algorithmes d'approximation).
Il existe un grand nombre de métaheuristiques différentes, allant de la simple recherche locale à des algorithmes complexes de recherche globale. Ces méthodes utilisent cependant un haut niveau d’abstraction, leur permettant d’être adaptées à une large gamme de problèmes différents.
Sommaire
Généralités
Terminologies
On parle de méta, du grec « au-delà » (comprendre ici « à un plus haut niveau »), heuristique, du grec ευρισκειν / heuriskein, qui signifie « trouver ». En effet, ces algorithmes se veulent des méthodes génériques pouvant optimiser une large gamme de problèmes différents, sans nécessiter de changements profonds dans l’algorithme employé.
Une terminologie légèrement différente considère que les méta-heuristiques sont une forme d’algorithmes d’optimisation stochastique, hybridés avec une recherche locale. Le terme méta est donc pris au sens où les algorithmes peuvent regrouper plusieurs heuristiques. On rencontre cette définition essentiellement dans la littérature concernant les algorithmes évolutionnaires, où elle est utilisée pour désigner une spécialisation. Dans le cadre de la première terminologie, un algorithme évolutionnaire hybridé avec une recherche locale sera plutôt désigné sous le terme d’algorithme mémétique.
Les métaheuristiques sont souvent inspirées par des systèmes naturels, qu’ils soient pris en physique (cas du recuit simulé), en biologie de l’évolution (cas des algorithmes génétiques) ou encore en éthologie (cas des algorithmes de colonies de fourmis ou de l’optimisation par essaims particulaires).
Nomenclature
Le but d’une métaheuristique est de résoudre un problème d’optimisation donné : elle cherche un objet mathématique (une permutation, un vecteur, etc.) minimisant (ou maximisant) une fonction objectif, qui décrit la qualité d’une solution au problème.
L’ensemble des solutions possibles forme l’espace de recherche. L’espace de recherche est au minimum borné, mais peut être également limité par un ensemble de contraintes.
Les métaheuristiques manipulent une ou plusieurs solutions, à la recherche de l’optimum, la meilleure solution au problème. Les itérations successives doivent permettre de passer d’une solution de mauvaise qualité à la solution optimale. L’algorithme s’arrête après avoir atteint un critère d’arrêt, consistant généralement en l’atteinte du temps d’exécution imparti ou en une précision demandée.
Une solution ou un ensemble de solutions est parfois appelé un état, que la métaheuristique fait évoluer via des transitions ou des mouvements. Si une nouvelle solution est construite à partir d’une solution existante, elle est sa voisine. Le choix du voisinage et de la structure de donnée le représentant peut être crucial.
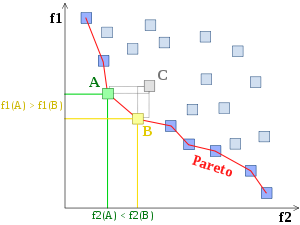
Lorsqu’une solution est associée à une seule valeur, on parle de problème mono-objectif, lorsqu’elle est associée à plusieurs valeurs, de problème multi-objectifs (ou multi-critères). Dans ce dernier cas, on recherche un ensemble de solutions non dominées (le « front de Pareto »), solutions parmi lesquelles on ne peut décider si une solution est meilleure qu’une autre, aucune n’étant systématiquement inférieure aux autres sur tous les objectifs.
Dans certains cas, le but recherché est explicitement de trouver un ensemble d’optimums « satisfaisants ». L’algorithme doit alors trouver l’ensemble des solutions de bonne qualité, sans nécessairement se limiter au seul optimum : on parle de méthodes multimodales.
Concepts généraux
Les métaheuristiques ne nécessitent pas de connaissances particulières sur le problème optimisé pour fonctionner, le fait de pouvoir associer une (ou plusieurs) valeurs à une solution est la seule information nécessaire.
En pratique, elles ne devraient être utilisées que sur des problèmes ne pouvant être optimisés par des méthodes mathématiques. Utilisées en lieu et place d’heuristiques spécialisées, elles montrent généralement de moins bonnes performances.
Les métaheuristiques sont souvent employées en optimisation combinatoire, mais on en rencontre également pour des problèmes continus ou mixtes (problèmes à variables discrètes et continues).
Certaines métaheuristiques sont théoriquement « convergentes » sous certaines conditions. Il est alors garanti que l’optimum global sera trouvé en un temps fini, la probabilité de ce faire augmentant asymptotiquement avec le temps. Cette garantie revient à considérer que l’algorithme se comporte au pire comme une recherche aléatoire pure (la probabilité de tenter toutes les solutions tendant vers 1). Cependant, les conditions nécessaires sont rarement vérifiées dans le cadre d’applications réelles. En pratique, la principale condition de convergence est de considérer que l’algorithme est ergodique (qu’il peut atteindre n’importe quelle solution à chaque mouvement), mais on se satisfait souvent d’une quasi-ergodicité (si la métaheuristique peut atteindre n’importe quelle solution en un nombre fini de mouvements).
Organisation générale
D’une manière générale, les métaheuristiques s’articulent autour de plusieurs notions :
- Voisinage ;
- Diversification/exploration ;
- Intensification/exploitation ;
- Mémoire et apprentissage.
Voisinage
Le voisinage d'une solution est un sous-ensemble de solutions qu'il est possible d'atteindre par une série de transformations données. Par extension on désigne parfois par le terme « voisinage » l'ensemble des transformations considérées.
Un voisinage simple pour le problème du voyageur de commerce sera, par exemple, l'ensemble des solutions qu'il est possible de construire en permutant deux villes dans une solution donnée.
La notion de voisinage est sans doute le principe général le plus utilisé pour la conceptions d’heuristiques. Pour les problèmes combinatoires, le voisinage a un impact important sur le comportement des métaheuristiques, alors que pour des problèmes continus, la notion même de voisinage est plus difficile à cerner.
Bien qu’il n’existe que très peu de résultats théoriques sur l’adéquation entre un voisinage et un problème discret donné, il peut être possible d’en calculer des indicateurs empiriques, comme la rugosité[1]. Les techniques les plus classiques concernant la définition d’un voisinage tournent autour des notions de permutations, de chaînes d’éjections et d’optimisations partielles.
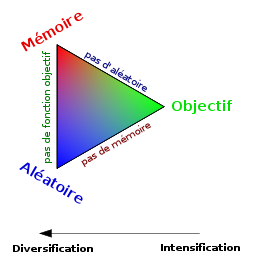
Intensification, diversification, apprentissage
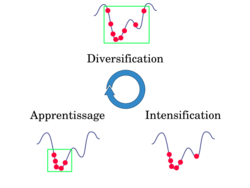
La diversification (ou exploration, synonyme utilisé presque indifféremment dans la littérature des algorithmes évolutionnaires) désigne les processus visant à récolter de l’information sur le problème optimisé. L'intensification (ou exploitation) vise à utiliser l’information déjà récoltée pour définir et parcourir les zones intéressantes de l’espace de recherche. La mémoire est le support de l’apprentissage, qui permet à l’algorithme de ne tenir compte que des zones où l’optimum global est susceptible de se trouver, évitant ainsi les optima locaux.
Les métaheuristiques progressent de façon itérative, en alternant des phases d’intensification, de diversification et d’apprentissage, ou en mélant ces notions de façon plus étroites. L’état de départ est souvent choisi aléatoirement, l’algorithme se déroulant ensuite jusqu’à ce qu’un critère d’arrêt soit atteint.
Les notions d’intensification et de diversifications sont prépondérantes dans la conception des métaheuristiques, qui doivent atteindre un équilibre délicat entre ces deux dynamiques de recherches. Les deux notions ne sont donc pas contradictoires, mais complémentaires, et il existe de nombreuses stratégies mélant à la fois l’un et l’autre des aspects.
Classification
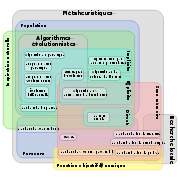 Les métaheuristiques peuvent être classées de nombreuses façons. Ce diagramme tente de présenter où se placent quelque unes des méthodes les plus connues. Un élement présenté à cheval sur différentes catégories indique que l'algorithme peut être placé dans l'une ou l'autre classe, selon le point de vue adopté.
Les métaheuristiques peuvent être classées de nombreuses façons. Ce diagramme tente de présenter où se placent quelque unes des méthodes les plus connues. Un élement présenté à cheval sur différentes catégories indique que l'algorithme peut être placé dans l'une ou l'autre classe, selon le point de vue adopté.
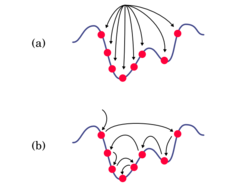
Parcours et population
Les métaheuristiques les plus classiques sont celles fondées sur la notion de parcours. Dans cette optique, l’algorithme fait évoluer une seule solution sur l’espace de recherche à chaque itération. La notion de voisinage est alors primordiale.
Les plus connues dans cette classe sont le recuit simulé, la recherche avec tabous, la recherche à voisinage variable, la méthode GRASP ou encore les méthode de bruitage.
Dans cette classification, l’autre approche utilise la notion de population. La métaheuristique manipule un ensemble de solutions en parallèle, à chaque itération.
On peut citer les algorithmes génétiques, l’optimisation par essaims particulaires, les algorithmes de colonies de fourmis.
La frontière est parfois floue entre ces deux classes. On peut ainsi considérer qu’un recuit simulé où la température baisse par paliers, a une structure à population. En effet, dans ce cas on manipule un ensemble de points à chaque palier, il s’agit simplement d’une méthode d’échantillonnage particulière.
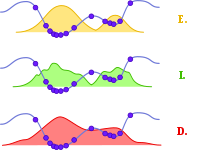
Emploi de mémoire
Les métaheuristiques utilisent l’historique de leur recherche pour guider l’optimisation aux itérations suivantes.
Dans le cas le plus simple, elles se limitent à considérer l’état de la recherche à une itération donnée pour déterminer la prochaine itération : il s’agit alors d’un processus de décision markovien, et on parlera de méthode sans mémoire. C’est le cas de la plupart des méthodes de recherche locale.
Beaucoup de métaheuristiques utilisent une mémoire plus évoluée, que ce soit sur le court terme (solutions visitées récemment, par exemple) ou sur le long terme (mémorisation d’un ensemble de paramètres synthétiques décrivant la recherche).
Fonction objectif statique ou dynamique
La plupart des métaheuristiques utilisent la fonction objectif en l’état, et font évoluer leur comportement de recherche de l’optimum. Cependant, certains algorithmes, comme la recherche locale guidée, modifient la représentation du problème, en incorporant l’information collectée durant la recherche, directement au sein de la fonction objectif.
Il est donc possible de classer les métaheuristiques selon qu’elles utilisent une fonction objectif statique (qui demeure inchangée tout au long de l’optimisation) ou dynamique (quand la fonction objectif est modifiée au cours de la recherche).
Nombre de structures de voisinage
La plupart des métaheuristiques utilisées dans le cadre des problèmes d’optimisation combinatoire utilisent une seule structure de voisinage. Cependant, des méthodes comme la recherche à voisinage variable permettent de changer de structure en cours de recherche.
Implicite, explicite, directe
En considérant les métaheuristiques comme des méthodes itératives utilisant un échantillonnage de la fonction objectif comme base d’apprentissage (définition plus particulièrement adaptée aux métaheuristiques à populations) apparaît le problème du choix de l’échantillonnage[2].
Dans la très grande majorité des cas, cet échantillonnage se fait sur une base aléatoire, et peut donc être décrit via une distribution de probabilités. Il existe alors trois classes de métaheuristiques, selon l’approche utilisée pour manipuler cette distribution.
La première classe est celle des méthodes implicites, où la distribution de probabilité n’est pas connue a priori. C’est le cas par exemple des algorithmes génétiques, où le choix de l’échantillonnage entre deux itérations ne suit pas une loi donnée, mais est fonction de règles locales.
Par opposition, on peut donc classer les méthodes explicites, qui utilisent une distribution de probabilité choisie à chaque itération. C’est le cas des algorithmes à estimation de distribution.
Dans cette classification, le recuit simulé occupe une place particulière, puisqu’on peut considérer qu’il échantillonne la fonction objectif en utilisant directement celle-ci comme distribution de probabilité (les meilleures solutions ayant une probabilité plus grande d’être tirées). Il n’est donc ni explicite ni implicite, mais plutôt « direct ».
Évolutionnaire ou non
On trouve parfois une classification présentant les algorithmes d’optimisations stochastiques comme étant « évolutionnaires » (ou « évolutionnistes ») ou non. L’algorithme sera considéré comme faisant partie de la classe des algorithmes évolutionnaires s’il manipule une population via des opérateurs, selon un algorithme général donné.
Cette façon de présenter les métaheuristiques dispose d’une nomenclature adaptée : on parlera d’opérateurs pour toute action modifiant l’état d’une ou plusieurs solutions. Un opérateur construisant une nouvelle solution sera dénommé générateur, alors qu’un opérateur modifiant une solution existante sera appelé mutateur.
Dans cette optique, la structure générale des algorithmes évolutionnaires enchaîne des étapes de sélection, de reproduction (ou croisement), de mutation et enfin de remplacement. Chaque étape utilise des opérateurs plus ou moins spécifiques.
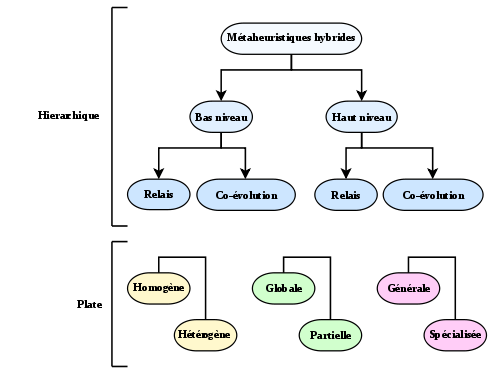
Taxinomie de l’hybridation
On parle d’hybridation quand la métaheuristique considérée est composée de plusieurs méthodes se répartissant les tâches de recherche. La taxinomie des métaheuristiques hybrides se sépare en deux parties : une classification hiérarchique et une classification plate. La classification est applicable aux méthodes déterministes aussi bien qu’aux métaheuristiques[3].
La classification hierarchique se fonde sur le niveau (bas ou haut) de l’hybridation et sur son application (en relais ou concurrente). Dans une hybridation de bas niveau, une fonction donnée d’une métaheuristique (par exemple, la mutation dans un algorithme évolutionnaire) est remplacée par une autre métaheuristique (par exemple une recherche avec tabou). Dans le cas du haut niveau, le fonctionnement interne « normal » des métaheuristiques n’est pas modifié. Dans une hybridation en relais, les métaheuristiques sont lancées les unes après les autres, chacune prenant en entrée la sortie produite par la précédente. Dans la concurrence (ou co-évolution), chaque algorithme utilise une série d’agents coopérants ensembles.
Cette première classification dégage quatre classes générales :
- bas niveau & relais (abrégé LRH en anglais),
- bas niveau & co-évolution (abrégé LCH),
- haut niveau & relais (HRH),
- haut niveau & co-évolution (HCH).
La seconde partie dégage plusieurs critères, pouvant caractériser les hybridations :
- si l’hybridation se fait entre plusieurs instances d’une même métaheuristique, elle est homogène, sinon, elle est hétérogène ;
- si les méthodes recherchent dans tout l’espace de recherche, on parlera d’hybridation globale, si elles se limitent à des sous-parties de l’espace, d’hybridation partielle ;
- si les algorithmes mis en jeu travaillent tous à résoudre le même problème, on parlera d’approche générale, s’ils sont lancés sur des problèmes différents, d’hybridation spécialisée.
Ces différentes catégories peuvent être combinées, la classification hierarchique étant la plus générale.
Applications
Les métaheuristiques sont souvent employées pour leur facilité de programmation et de manipulation. Elles sont en effet facilement adaptables à tout type de problème d’optimisation. Toutefois, elles sont le plus judicieusement employées sur des problèmes d’optimisation difficile, où des méthodes d’optimisation plus classiques (méthodes déterministes, notamment) montrent leurs limites.
De façon générale, on peut considérer que des problèmes présentant les caractéristiques suivantes sont assez propices à l’utilisation de métaheuristiques :
- NP-complétude,
- nombreux optima locaux,
- discontinuités,
- contraintes fortes,
- non dérivabilité,
- temps de calcul de la fonction objectif prohibitif,
- solution approchée souhaitée,
- etc.
Tests
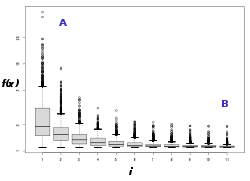
Pour tester une métaheuristique, une première étape consiste à utiliser des fonctions mathématiques spécialement conçues[4]. Les algorithmes sont évalués sur la base d’un ensemble de fonctions, plus ou moins difficiles, puis comparés entre eux.
Les métaheuristiques étant généralement stochastiques, les tests doivent en principe être répétés un grand nombre de fois, puis exploités via des méthodes statistiques. Cependant, cette pratique reste relativement peu répandue dans la littérature spécialisée.
Problèmes réels
Dans un numéro spécial de la revue scientifique European Journal of Operational Research, consacré aux applications des métaheuristiques[5], les éditeurs ont constatés que la majorité des 20 articles publiés le furent dans deux domaines : les problèmes d'ordonnancement et de logistique. Les méthodes les plus utilisés appartiennent à la famille des algorithmes évolutionnaires, souvent hybridés avec des méthodes de recherche locale.
Quelques exemples de problèmes concrets, optimisés via des métaheuristiques :
- problèmes de tournée de véhicules,
- optimisation de réseaux mobiles UMTS,
- gestion du trafic aérien,
- optimisation des plans de chargement des cœurs de réacteurs nucléaires,
- etc.
Avantages et inconvénients
Les métaheuristiques étant très généralistes, elles peuvent être adaptées à tout type de problème d’optimisation pouvant se réduire à une « boîte noire ». Elles sont souvent moins puissantes que des méthodes exactes sur certains types de problèmes. Elles ne garantissent pas non plus la découverte de l’optimum global en un temps fini. Cependant, un grand nombre de problèmes réels n’est pas optimisable efficacement par des approches purement mathématiques, les métaheuristiques peuvent alors être utilisées avec profit.
La notion d’efficacité se rapporte généralement à deux objectifs contradictoires : la vitesse et la précision. La vitesse est souvent mesurée en nombre d’évaluations de la fonction objectif, qui est la plupart du temps la partie la plus gourmande en temps de calcul. La précision se rapporte à la distance entre l’optimum trouvé par la métaheuristique et l’optimum réel, soit du point de vue de la solution, soit de celui de la valeur. Bien souvent, un algorithme rapide est peu précis, et inversement.
Généralement, un choix doit être fait quant au critère d’arrêt adéquat. Un nombre d’évaluation ou un temps imparti est souvent utilisé, mais on peut également choisir d’atteindre une valeur donnée de la fonction objectif (le but étant alors de trouver une solution associée). Il est également possible de choisir des critères dépendants du comportement de l’algorithme, comme une dispersion minimale de la population de points ou un paramètre interne approprié. En tout état de cause, le choix du critère d’arrêt influencera la qualité de l’optimisation.
L’utilisation de métaheuristiques peut paraître relativement simple, en première approche, mais il est souvent nécessaire d’adapter l’algorithme au problème optimisé. Tout d’abord, principalement dans le cadre de l’optimisation combinatoire, le choix de la représentation des solutions manipulées peut être crucial. Ensuite, la plupart des métaheuristiques disposent de paramètres dont le réglage n’est pas nécessairement trivial. Enfin, obtenir de bonnes performances passe généralement par une étape d’adaptation des diverses étapes de l’algorithme (initialisation, notamment). En pratique, seul le savoir-faire et l’expérience de l’utilisateur permet de gérer ces problèmes.
Il est admis que, d’un point de vue très général, aucune métaheuristique n’est réellement meilleure qu’une autre. En effet, une métaheuristique ne peut prétendre être plus efficace sur tous les problèmes, bien que certaines instances (c’est-à-dire l’algorithme lui même, mais aussi un choix de paramètres et une implémentation donnée) puissent être plus adaptées que d’autres sur certaines classes de problèmes. Cette constatation est décrite par le théorème du no free lunch (« pas de dîner gratuit »).
En dernière analyse, il est parfois possible que le choix de la représentation des solutions, ou plus généralement des méthodes associées à la métaheuristique, ait plus d’influence sur les performances que le type d’algorithme lui-même. En pratique, cependant, les métaheuristiques se montrent plus puissantes que les méthodes de parcours exhaustif ou de recherche purement aléatoire.
Variantes
Liste de métaheuristiques
Les métaheuristiques les plus connues sont :
- Les algorithmes évolutionnistes, parmi lesquels :
- les stratégies d’évolution,
- les algorithmes génétiques,
- les algorithmes à évolution différentielle,
- les algorithmes à estimation de distribution,
- les systèmes immunitaires artificiels,
- la recomposition de chemin (Path relinking en anglais)
- le recuit simulé,
- les algorithmes de colonies de fourmis,
- Les algorithmes d’optimisation par essaims particulaires,
- la recherche avec tabous,
- la méthode GRASP.
Il existe un très grand nombre d’autres métaheuristiques, plus ou moins connues :
- l’algorithme du kangourou,
- la méthode de Fletcher et Powell,
- la méthode du bruitage,
- la tunnelisation stochastique,
- l’escalade de collines à recommencements aléatoires,
- la méthode de l'entropie croisée,
- etc.
La recherche dans le domaine étant très active, il est impossible de produire une liste exhaustive des différentes métaheuristiques d’optimisation. La littérature spécialisée montre un grand nombre de variantes et d’hybridations entre méthodes, particulièrement dans le cas des algorithmes évolutionnaires.
Historique
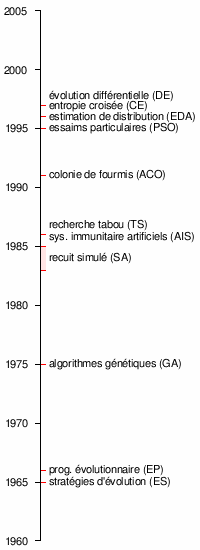
Chronologie des principales métaheuristiques, le nom est indiqué suivi de l’acronyme anglais entre parenthèses.
- 1952 : premiers travaux sur l’utilisation de méthodes stochastiques pour l’optimisation[6].
- 1954 : Barricelli effectue les premières simulations du processus d’évolution et les utilise sur des problèmes d’optimisation généraux[7].
- 1965 : Rechenberg conçoit le premier algorithme utilisant des stratégies d’évolution[8].
- 1966 : Fogel, Owens et Walsh proposent la programmation évolutionnaire[9].
- 1970 : Hastings propose l’algorithme de Metropolis-Hastings, permettant d’échantillonner n’importe-quelle distribution de probabilité[10].
- 1970 : John Horton Conway conçoit le jeu de la vie, l’automate cellulaire le plus connu à ce jour.
- 1975 : travaillant sur les automates cellulaires, Holland propose les premiers algorithmes génétiques[11].
- 1980 : Smith utilise la programmation génétique [12].
- 1983 : s’appuyant sur les travaux d’Hastings, Kirkpatrick, Gelatt et Vecchi concoivent le recuit simulé[13].
- 1985 : indépendamment de ceux-ci, Černý propose le même algorithme[14].
- 1986 : La première mention du terme méta-heuristique est faite par Fred Glover, lors de la conception de la recherche tabou[15] :
- « La recherche avec tabou peut être vue comme une "méta-heuristique", superposée à une autre heuristique. L'approche vise à éviter les optimums locaux par une stratégie d'interdiction (ou, plus généralement, de pénalisation) de certains mouvements. »
- 1986 : Farmer, Packard et Perelson travaillent sur les systèmes immunitaire artificiels[16].
- 1988 : la première conférence sur les algorithmes génétiques est organisée à l’université de l’Illinois à Urbana-Champaign.
- 1988 : des travaux sur le comportement collectif des fourmis trouvent une application en intelligence artificielle[17].
- 1988 : Koza dépose son premier brevet sur la programmation génétique[18].
- 1989 : Goldberg publie un des livres les plus connus sur les algorithmes génétiques[19].
- 1989 : Evolver, le premier logiciel d’optimisation par algorithmes génétiques est publié par la société Axcelis.
- 1989 : le terme algorithme mémétique apparait[20].
- 1991 : Les algorithmes de colonie de fourmis sont proposées par Marco Dorigo, dans sa thèse de doctorat[21].
- 1993 : le terme « Evolutionary Computation » (calcul évolutionnaire en français) se répand, avec la parution de la revue éponyme, publiée par le Massachusetts Institute of Technology.
- 1995 : Feo et Resende proposent la méthode GRASP (pour Greedy randomized adaptive search procedure, « procédure de recherche avide aléatoire adaptative » en français)[22].
- 1995 : Kennedy et Eberhart concoivent l’optimisation par essaims particulaires[23],[24].
- 1996 : Mühlenbein et Paaß proposent les algorithmes à estimation de distribution[25].
- 1997 : Storn et Price proposent un algorithme à évolution différentielle[26].
- 1997 : Rubinstein conçoit la méthode de l’entropie croisée[27].
- 1999 : Boettcher propose l’optimisation extrêmale[28].
- 2000 : premiers algorithmes génétiques interactifs[29].
Extensions
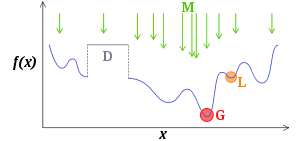
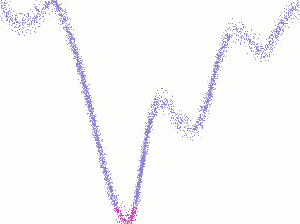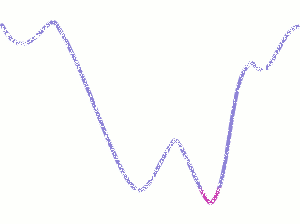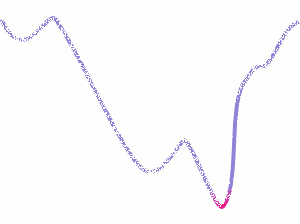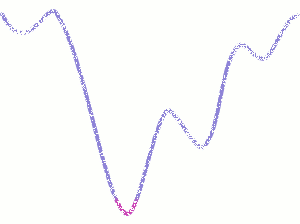 Exemple de problème d’optimisation continue, dynamique et bruité.
Exemple de problème d’optimisation continue, dynamique et bruité.
Les métaheuristiques, de part leur nature flexible, se prêtent particulièrement à des extensions. On peut ainsi trouver des adaptations pour des problèmes plus complexe que l’optimisation mono-objectif :
- problèmes multi-objectifs (plusieurs objectifs contradictoires doivent être optimisés de concert),
- optimisation multi-modale (plusieurs optimums doivent être trouvés),
- optimisation en environnement incertain (un bruit est présent sur la valeur renvoyée par la fonction objectif, ou sur le passage des paramètres à celle-ci),
- hybridations entre métaheuristiques,
- hybridations avec des méthodes exactes,
- problèmes dynamiques (la fonction objectif change durant le temps de l’optimisation),
- gestion de contraintes fortement non-linéaires,
- combinaison des problèmes précédents,
- etc.
Références
Sources
- (fr) Jacques Teghem et Marc Pilrot (éditeurs), Optimisation approchée en recherche opérationnelle, Hermes, traité I2C, mai 2002. ISBN 2746204622
- (fr) Yann Collette, Patrick Siarry, Optimisation multi-objectif, Éd. Eyrolles, Paris, 2002, Broché, 322 pages, ISBN 2-212-11168-1.
- (fr) Johann Dréo, Alain Petrowski, Éric Taillard, Patrick Siarry, Métaheuristiques pour l’optimisation difficile, Français, Éd. Eyrolles, Paris, septembre 2003, Broché, 356 pages, ISBN 2-212-11368-4.
- (en) Pierre Collet, Jean-Philippe Rennard, Introduction to Stochastic Optimization Algorithms, dans Handbook of Research on Nature-Inspired Computing for Economics and Management, édité par J.-P. Rennard, IDEA Group Inc, septembre 2006, Relié, 1100 pages, ISBN 1591409845.
- (en) Christian Blum, Andrea Roli, Metaheuristics in combinatorial optimization : Overview and conceptual comparison, ACM Computing Surveys, volume 35, numéro 3, septembre 2003, pages 268-308. DOI:10.1145/937503.937505
- ↑ V. Angel, La rugosité des paysages : une théorie pour la difficulté des problèmes d’optimisation combinatoire relativement aux métaheuristiques, thèse de doctorat de l’université de Paris-Sud, Orsay, 1998.
- ↑ J. Dreo, J.-P. Aumasson, W. Tfaili, P. Siarry, Adaptive Learning Search, a new tool to help comprehending metaheuristics, to appear in the International Journal on Artificial Intelligence Tools.
- ↑ El-Ghazali Talbi, A taxonomy of hybrid metaheuristics, Journal of Heuristics, volume 8, no 2, pages 541-564, septembre 2002
- ↑ (en) exemples de fonctions de tests pour métaheuristiques d’optimisation de problèmes continus.
- ↑ W. Dullaert, M. Sevaux, K. Sörensen et J. Springael, Applications of metaheuristics, numéro spécial du European Journal of Operational Research, no 179, 2007.
- ↑ Robbins, H. and Monro, S., A Stochastic Approximation Method, Annals of Mathematical Statistics, vol. 22, pp. 400-407, 1951
- ↑ Barricelli, Nils Aall, Esempi numerici di processi di evoluzione, Methodos, pp. 45-68, 1954
- ↑ Rechenberg, I., Cybernetic Solution Path of an Experimental Problem, Royal Aircraft Establishment Library Translation, 1965
- ↑ Fogel, L., Owens, A.J., Walsh, M.J., Artificial Intelligence through Simulated Evolution, Wiley, 1966
- ↑ W.K. Hastings. Monte Carlo Sampling Methods Using Markov Chains and Their Applications, Biometrika, volume 57, no 1, pages 97-109, 1970
- ↑ Holland, John H., Adaptation in Natural and Artificial Systems, University of Michigan Press, Ann Arbor, 1975
- ↑ Smith, S.F., A Learning System Based on Genetic Adaptive Algorithms, PhD dissertation (University of Pittsburgh), 1980
- ↑ S. Kirkpatrick, C. D. Gelatt et M. P. Vecchi, Optimization by Simulated Annealing, Science, volume 220, no 4598, pages 671-680, 1983
- ↑ V. Cerny, A thermodynamical approach to the travelling salesman problem : an efficient simulation algorithm Journal of Optimization Theory and Applications, volume45, pages 41-51, 1985
- ↑ Fred GLover, Future Paths for Integer Programming and Links to Artificial Intelligence, Comput. & Ops. Res.Vol. 13, No.5, pp. 533-549, 1986
- ↑ J.D. Farmer, N. Packard and A. Perelson, The immune system, adaptation and machine learning, Physica D, vol. 22, pp. 187--204, 1986
- ↑ F. Moyson, B. Manderick, The collective behaviour of Ants : an Example of Self-Organization in Massive Parallelism, Actes de AAAI Spring Symposium on Parallel Models of Intelligence, Stanford, Californie, 1988
- ↑ Koza, John R. Non-Linear Genetic Algorithms for Solving Problems. United States Patent 4,935,877. Filed May 20, 1988. Issued June 19, 1990
- ↑ Goldberg, David E., Genetic Algorithms in Search, Optimization and Machine Learning, Kluwer Academic Publishers, Boston, MA., 1989
- ↑ P. Moscato, On Evolution, Search, Optimization, Genetic Algorithms and Martial Arts : Towards Memetic Algorithms, Caltech Concurrent Computation Program, C3P Report 826, 1989.
- ↑ M. Dorigo, Optimization, Learning and Natural Algorithms, Thèse de doctorat, Politecnico di Milano, Italie, 1992.
- ↑ Feo, T., Resende, M., Greedy randomized adaptive search procedure, Journal of Global Optimization, tome 42, page 32--37, 1992
- ↑ Eberhart, R. C. et Kennedy, J., A new optimizer using particle swarm theory, Proceedings of the Sixth International Symposium on Micromachine and Human Science, Nagoya, Japan. pp. 39-43, 1995
- ↑ Kennedy, J. et Eberhart, R. C., Particle swarm optimization, Proceedings of IEEE International Conference on Neural Networks, Piscataway, NJ. pp. 1942-1948, 1995
- ↑ Mülhenbein, H., Paaß, G., From recombination of genes to the estimation of distribution I. Binary parameters, Lectures Notes in Computer Science 1411: Parallel Problem Solving from Nature, tome PPSN IV, pages 178--187, 1996
- ↑ Rainer Storn, Kenneth Price, Differential Evolution – A Simple and Efficient Heuristic for global Optimization over Continuous Spaces, Journal of Global Optimization, volume 11, no 4, pages 341-359, 1997
- ↑ Rubinstein, R.Y., Optimization of Computer simulation Models with Rare Events, European Journal of Operations Research, 99, 89-112, 1997
- ↑ Stefan Boettcher, Allon G. Percus, "Extremal Optimization : Methods derived from Co-Evolution", Proceedings of the Genetic and Evolutionary Computation Conference (1999)
- ↑ Takagi, H., Active user intervention in an EC Search, Proceesings of the JCIS 2000
En savoir plus
Bibliographie :
- (en) El-Ghazali Talbi, Metaheuristics: from design to implementation, Wiley, 2009. ISBN 978-0-470-27858-1 (624p)
- (en) Bibliographie d’introduction aux métaheuristiques (2003)
Sites généralistes :
Logiciels et frameworks :
- Portail de l’informatique
Catégories : Métaheuristique | Recherche opérationnelle
Wikimedia Foundation. 2010.